数学の公式・定理集｜２次関数

04/07/2022公式・定理,数学１

1. ２次関数
2. おすすめの数学辞典

２次関数

２次関数のグラフ

２次関数の式

$a \neq 0$ とする。

一般形

$\begin{equation*} \quad y=a{x}^{\scriptsize{2}}+bx+c \end{equation*}$

標準形

$\begin{equation*} \quad y=a{\left( x-p \right)}^{\scriptsize{2}}+q \end{equation*}$

標準形のグラフ

標準形 $y=a{\left( x-p \right)}^{\scriptsize{2}}+q \ (a \neq 0)$ のグラフ

頂点の座標が

$(p \ , \ q )$

軸が直線

$x=p$

の放物線

$a \gt 0$ なら下に凸

$a \lt 0$ なら上に凸

一般形のグラフ

一般形 $y=a{x}^{\scriptsize{2}}+bx+c \quad (a \neq 0)$ のグラフ

右辺を平方完成して標準形に変形する

$\begin{equation*} \quad y=a{\left( x+ \frac{b}{2a} \right)}^{\scriptsize{2}}-\frac{b^{\scriptsize{2}}-4ac}{4a} \end{equation*}$

頂点の座標が

$\begin{equation*} \quad \left(-\frac{b}{2a} \ , \ -\frac{b^{\scriptsize{2}}-4ac}{4a} \right) \end{equation*}$

軸が直線

$\begin{equation*} \quad x=-\frac{b}{2a} \end{equation*}$

の放物線

$a \gt 0$ なら下に凸

$a \lt 0$ なら上に凸

平行移動、対称移動

平行移動

$x$ 軸方向に

$p$ 、

$y$ 軸方向に

$q$ だけ平行移動すると

点

$(a \ , \ b)$

$\longrightarrow \ (a+p \ , \ b+q)$

グラフ

$y=f(x)$

$\longrightarrow \ y=f(x-p)+q$

２次関数｜２次関数のグラフの平行移動について

対称移動

	$x$ 軸	$y$ 軸	原点
点 $(a \ , \ b)$	$(a \ , \ -b)$	$(-a \ , \ b)$	$(-a \ , \ -b)$
グラフ $y=f(x)$	$y=-f(x)$	$y=f(-x)$	$y=-f(-x)$

点やグラフの対称移動

関数の最大・最小

２次関数の最大・最小

平方完成して標準形にする。
- $y=a{\left( x-p \right)}^{\scriptsize{2}}+q$
凸の向きを調べる。
- ① a \gt 0 のとき
  - $x=p$ で最小値 $q$
  - 最大値はなし
- ② a\lt 0 のとき
  - $x=p$ で最大値 $q$
  - 最小値はなし

２次関数(定義域あり)の最大・最小

$a \gt 0$ (下に凸)の場合

頂点が区間の内にあるとき
- 最小：頂点
- 最大：頂点から遠い方の区間の端
頂点が区間の外にあるとき
- 最小：頂点に近い方の区間の端
- 最大：頂点から遠い方の区間の端

上に凸の場合と逆になる。

$a \lt 0$ (上に凸)の場合

頂点が区間の内にあるとき
- 最小：頂点から遠い方の区間の端
- 最大：頂点
頂点が区間の外にあるとき
- 最小：頂点から遠い方の区間の端
- 最大：頂点に近い方の区間の端

下に凸の場合と逆になる。

２次関数の決定

与えられた条件によって一般形と標準形を使い分ける。

与えられた条件が放物線の頂点や軸

$\rightarrow y=a{\left( x-p \right)}^{\scriptsize{2}}+q$ とおく。

与えられた条件がグラフが通る３点

$\rightarrow y=a{x}^{\scriptsize{2}}+bx+c$ とおく。

２次関数｜２次関数の決定について

２次方程式の実数解の個数

２次方程式 $a{x}^{\scriptsize{2}}+bx+c=0$ の判別式 $D=b^{\scriptsize{2}}-4ac$ の値を求める。

$D \gt 0$ ⇔ 異なる２つの実数解をもつ

$D = 0$ ⇔ ただ１つの実数解(重解)をもつ

$D \lt 0$ ⇔ 実数解をもたない

２次関数のグラフとｘ軸

２次関数 $y=a{x}^{\scriptsize{2}}+bx+c$ のグラフを $C$ とし、 $y=0$ のときの２次方程式 $a{x}^{\scriptsize{2}}+bx+c=0$ の判別式を $D=b^{\scriptsize{2}}-4ac$ とする。

$D \gt 0$ ⇔ Ｃはｘ軸と異なる２点で交わる(共有点２個)

$D = 0$ ⇔ Ｃはｘ軸と１点で接する(共有点１個)

$D \lt 0$ ⇔ Ｃはｘ軸と共有点をもたない

２次関数｜２次関数のグラフとx軸との位置関係について

２次不等式

$a{x}^{\scriptsize{2}}+bx+c \gt 0 \ , \ a{x}^{\scriptsize{2}}+bx+c \lt 0$ の解

２次方程式 $a{x}^{\scriptsize{2}}+bx+c = 0$ が、異なる２つの実数解 $\alpha \ , \ \beta$ をもち $\alpha \lt \beta$ とする（ただし、 $a \gt 0$ ）

$a{x}^{\scriptsize{2}}+bx+c \gt 0$ の解

$\quad x \lt \alpha \ , \ \beta \lt x$

$a{x}^{\scriptsize{2}}+bx+c \geqq 0$ の解

$\quad x \leqq \alpha \ , \ \beta \leqq \ x$

$a{x}^{\scriptsize{2}}+bx+c \lt 0$ の解

$\quad \alpha \lt x \lt \beta$

$a{x}^{\scriptsize{2}}+bx+c \leqq 0$ の解

$\quad \alpha \leqq x \leqq \beta$

${\left(x- \alpha \right)}^{\scriptsize{2}} \gt 0 \ , \ {\left(x- \alpha \right)}^{\scriptsize{2}} \lt 0$ の解

${\left(x- \alpha \right)}^{\scriptsize{2}} \lt 0$ の解
解なし

${\left(x- \alpha \right)}^{\scriptsize{2}} \leqq 0$ の解

$\quad x = \alpha$

${\left(x- \alpha \right)}^{\scriptsize{2}} \gt 0$ の解

$\quad \alpha$ 以外のすべての実数

${\left(x- \alpha \right)}^{\scriptsize{2}} \geqq 0$ の解
すべての実数

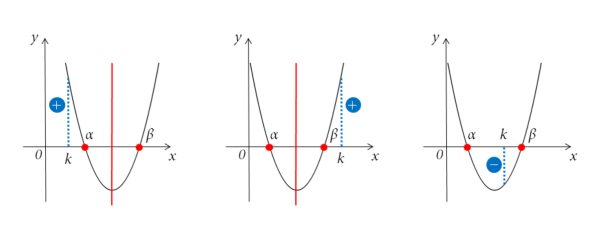
放物線とx軸の共有点の位置

$a \gt 0$ のとき

$\begin{align*} &\quad f(x)=a{x}^{2}+bx+c \ (a \neq 0) \\[ 7pt ] &\quad D=b^{2}-4ac \end{align*}$

とする。

また、放物線

$y=f(x)$ が

$x$ 軸と

$x=\alpha \ , \ \beta \ (\alpha \leqq \beta)$ で共有点をもつとする。

\alpha \gt k \ , \ \beta \gt k
- $\Longleftrightarrow D \geqq 0 \ , \ \text{軸} \gt k \ , \ f(k) \gt 0$
\alpha \lt k \ , \ \beta \lt k
- $\Longleftrightarrow D \geqq 0 \ , \ \text{軸} \lt k \ , \ f(k) \gt 0$
\alpha \lt k \lt \beta
- $\Longleftrightarrow f(k) \lt 0$

数学Ｉ・Ａ｜2017センター試験・第１問を解いてみよう