数学２
今回は、２次方程式の解が存在する範囲について学習しましょう。
２次方程式の係数と、解の符号との関係をすでに学習していますが、その応用になります。応用的な内容なので難しく感じるかもしれませんが、じっくり腰を据えて取り組みましょう。
２次方程式の解の存在範囲
２次方程式の解の存在範囲については、数学１の単元（２次不等式）で基本的な事柄を学習しています。２次関数のグラフとｘ軸の共有点の位置についてです。
ここでは、２次方程式の解が、特定の実数との大小関係を満たして存在する範囲を調べます。これまでであれば、判別式や軸の方程式などから条件を導きました。ここでは、２次方程式の解に注目します。
本題に入る前に、２次関数のグラフを用いた調べ方を確認しておきましょう。以下、２次関数のグラフを単に「放物線」と言うことがあります。
２次関数のグラフ（放物線）を用いた調べ方
２次関数の式において、ｙ＝０とおくと、ｘについての２次方程式となります。この２次方程式が実数解α，βをもつときを考えます。
ｙ＝０のときのｘの値が２次方程式の実数解です。これは、放物線とｘ軸との共有点のｘ座標に相当します。
放物線と２次方程式にはこのような対応関係があるので、放物線とｘ軸の位置関係を考えれば、実数解α，βが存在する範囲を調べることができます。このことは、実数解の符号でも同じ要領で調べています。
２次方程式の実数解とある実数ｋとの大小関係を考えるとしましょう。このとき、大小関係は３通り考えられます。
実数解とある実数との大小関係は３通り
- ２つの実数解α，βがともに実数ｋより大きい
- ２つの実数解α，βがともに実数ｋより小さい
- ２つの実数解α，βの間に実数ｋがある
それぞれの場合について、どんな条件が成り立つのかをグラフを用いて考えます。このとき、考えやすいように２次の係数を正にしておき、下に凸のグラフで考えます。
２つの実数解がともに実数ｋより大きい場合
２つの実数解がともに実数ｋより大きい場合を考えてみましょう。放物線を図示すると以下のようになります。
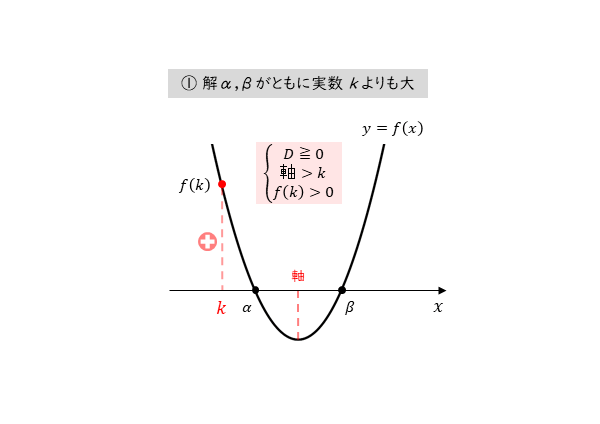解α，βがともに実数ｋよりも大きい 放物線とｘ軸の位置関係から、３つの条件を導くことができます。
[１] ２つの実数解がともに実数ｋより大
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 7pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \quad (\alpha \lt \beta) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を $D$ とし、} \\[ 5pt ]
&\quad f(x)=ax^{\scriptsize{2}}+bx+c \quad (a \gt 0) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{$2$ 次方程式 $f(x)=0$ の実数解 $\alpha \ , \ \beta$ が} \\[ 5pt ]
&\text{ともに実数 $k$ より大きくなるのは} \\[ 5pt ]
&\quad D \geqq 0 \\[ 7pt ]
&\quad \text{軸} \ -\frac{b}{2a} \gt k \\[ 7pt ]
&\quad f(k) \gt 0 \\[ 7pt ]
&\text{が成り立てばよい。} \\[ 5pt ]
&\text{したがって} \\[ 5pt ]
&\quad \alpha \gt k \ \text{かつ} \ \beta \gt k \\[ 7pt ]
&\quad \Leftrightarrow \ D \geqq 0 \ , \ \text{軸} \ -\frac{b}{2a} \gt k \ , \ f(k) \gt 0
\end{align*}
判別式の条件については、「異なる２つの～」という文言がないので等号を含みます（以下、同様です）。
２つの実数解がともに実数ｋより小さい場合
２つの実数解がともに実数ｋより小さい場合を考えてみましょう。放物線を図示すると以下のようになります。
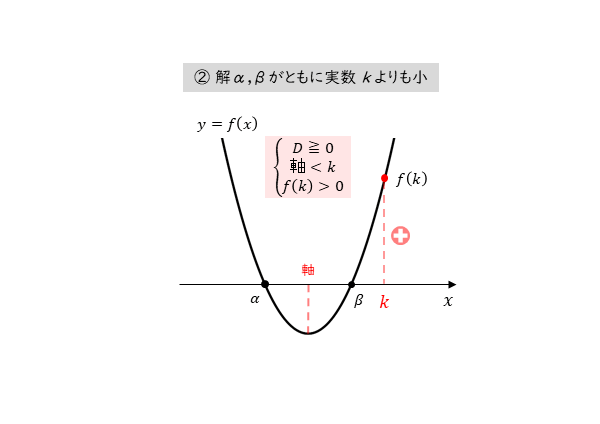解α，βがともに実数ｋよりも小さい 放物線とｘ軸との位置関係から、３つの条件を導くことができます。
[２] ２つの実数解がともに実数ｋより小
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 7pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \quad (\alpha \lt \beta) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を $D$ とし、} \\[ 5pt ]
&\quad f(x)=ax^{\scriptsize{2}}+bx+c \quad (a \gt 0) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{$2$ 次方程式 $f(x)=0$ の実数解 $\alpha \ , \ \beta$ が} \\[ 5pt ]
&\text{ともに実数 $k$ より小さくなるのは} \\[ 5pt ]
&\quad D \geqq 0 \\[ 7pt ]
&\quad \text{軸} \ -\frac{b}{2a} \lt k \\[ 7pt ]
&\quad f(k) \gt 0 \\[ 7pt ]
&\text{が成り立てばよい。} \\[ 5pt ]
&\text{したがって} \\[ 5pt ]
&\quad \alpha \lt k \ \text{かつ} \ \beta \lt k \\[ 7pt ]
&\quad \Leftrightarrow \ D \geqq 0 \ , \ \text{軸} \ -\frac{b}{2a} \lt k \ , \ f(k) \gt 0
\end{align*}
実数ｋより大きい場合との違いは、軸の条件（符号の向きが異なる）です。
２つの実数解が実数ｋの間にある場合
２つの実数解が実数ｋの間にある場合を考えてみましょう。放物線を図示すると以下のようになります。
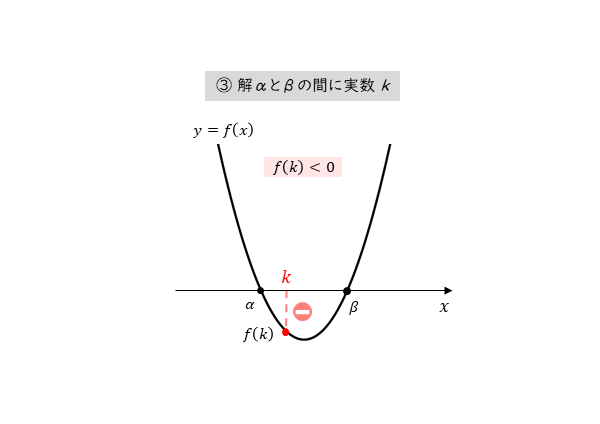２つの実数解が実数ｋの間にある 放物線とｘ軸との位置関係から、ただ１つの条件を導くことができます。
[３] ２つの実数解が実数ｋの間る
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 7pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \quad (\alpha \lt \beta) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を $D$ とし、} \\[ 5pt ]
&\quad f(x)=ax^{\scriptsize{2}}+bx+c \quad (a \gt 0) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{$2$ 次方程式 $f(x)=0$ の実数解 $\alpha \ , \ \beta$ が} \\[ 5pt ]
&\text{実数 $k$ の間にあるのは} \\[ 5pt ]
&\quad f(k) \lt 0 \\[ 7pt ]
&\text{が成り立てばよい。} \\[ 5pt ]
&\text{したがって} \\[ 5pt ]
&\quad \alpha \lt k \lt \beta \\[ 7pt ]
&\quad \Leftrightarrow \ f(k) \lt 0
\end{align*}
２つの実数解α，βが実数ｋの間にある場合、条件は１つだけです。このとき、２次方程式の解は必ず異なる２つの実数解となるので、判別式の条件は不要です。
３通りの場合について、まとめると以下のようになります。
２次方程式の解の存在範囲
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 7pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \quad (\alpha \lt \beta) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を $D$ とし、} \\[ 5pt ]
&\quad f(x)=ax^{\scriptsize{2}}+bx+c \quad (a \gt 0) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&[1] \ \alpha \gt k \ \text{かつ} \ \beta \gt k \\[ 7pt ]
&\qquad \Leftrightarrow \ D \geqq 0 \ , \ \text{軸} \ -\frac{b}{2a} \gt k \ , \ f(k) \gt 0 \\[ 10pt ]
&[2] \ \alpha \lt k \ \text{かつ} \ \beta \lt k \\[ 7pt ]
&\qquad \Leftrightarrow \ D \geqq 0 \ , \ \text{軸} \ -\frac{b}{2a} \lt k \ , \ f(k) \gt 0 \\[ 10pt ]
&[3] \ \alpha \lt k \lt \beta \\[ 7pt ]
&\qquad \Leftrightarrow \ f(k) \lt 0 \\[ 7pt ]
&\text{ただし、$[3]$ のとき、$D \gt 0$ が成り立つので、} \\[ 5pt ]
&\text{判別式の条件は不要。}
\end{align*}
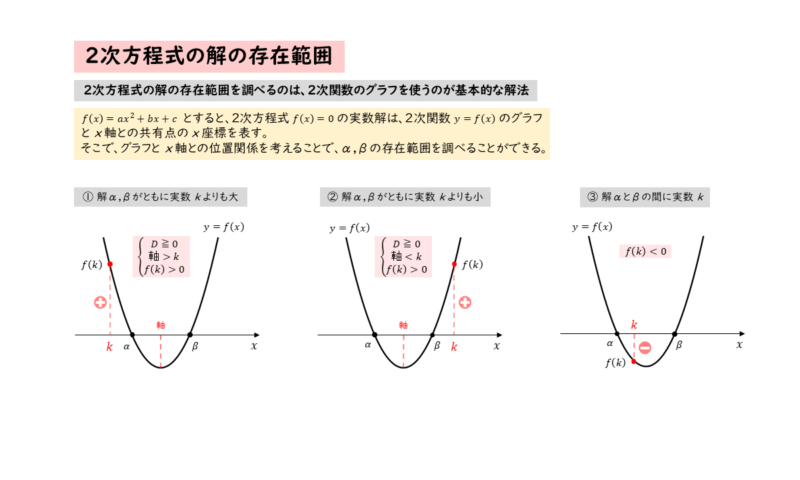２次方程式の解の存在範囲まとめ 以上が数学１で学習した内容になります。ここからがこの単元の本題になります。
２つの実数解の和と積を用いるのは間違い
２次方程式の実数解と実数ｋとの大小関係を考えるとき、実数解の和と差を利用するとします。簡単そうに見えますが、そうでもありません。
２次方程式の実数解の符号のときと同じようにはいきません。同じ要領で得られた条件は間違いです。この間違いは意外と多いので要注意です。
よくある間違い
\begin{align*}
&\text{$2$ 次方程式 $f(x)=0$ の実数解がともに} \\[ 5pt ]
&\text{実数 $k$ より大きくなるのは、判別式を} \\[ 5pt ]
&\text{$D$ とすると} \\[ 5pt ]
&\quad D \geqq 0 \\[ 7pt ]
&\quad \alpha+\beta \gt 2k \\[ 7pt ]
&\quad \alpha \beta \gt k^{\scriptsize{2}} \\[ 7pt ]
&\text{が成り立てばよい。}
\end{align*}
２つの実数解α，βがともに実数ｋよりも大きくなるので、和が２ｋよりも大きくなり、積がｋ2よりも大きくなれば良いと考えてしまいます。確かにこのことは間違いではありません。しかし、その逆は成り立つでしょうか？
２つの実数解α，βの和が２ｋよりも大きく、積がｋ2よりも大きいとき、２つの実数解α，βがともに実数ｋよりも大きくなるでしょうか。実数ｋを具体的な数で考えてみると間違いに気付きます。
よくある間違い 例)ｋ＝２のとき
\begin{align*}
&\text{$2$ 次方程式 $f(x)=0$ の実数解がともに} \\[ 5pt ]
&\text{$2$ より大きくなるとき、} \\[ 5pt ]
&\quad \alpha \gt 2 \ , \ \beta \gt 2 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad \alpha \gt 2 \ , \ \beta \gt 2 \\[ 7pt ]
&\quad \Rightarrow \ \alpha+\beta \gt 4 \ , \ \alpha \beta \gt 4 \\[ 7pt ]
&\text{は成り立つ。この逆を考えると}\\[ 5pt ]
&\quad \alpha+\beta \gt 4 \ , \ \alpha \beta \gt 4 \\[ 7pt ]
&\quad \Rightarrow \ \alpha \gt 2 \ , \ \beta \gt 2 \\[ 7pt ]
&\text{は成り立たない。反例は}\\[ 5pt ]
&\quad \alpha=1 \ , \ \beta=5 \\[ 7pt ]
&\text{がある。} \\[ 5pt ]
&\text{したがって、$\alpha \gt k \ , \ \beta \gt k$ のとき} \\[ 5pt ]
&\quad \alpha+\beta \gt 2k \ , \ \alpha \beta \gt k^{\scriptsize{2}} \\[ 7pt ]
&\text{は等価な条件にはならない。}
\end{align*}
実数ｋを具体的な値で考えてみると、２つの実数解の和と積を用いた場合、もとのαとβの条件を満たさない組み合わせまで含んでしまうことが分かります。
２次方程式の実数解と実数ｋとの大小関係では、単純に実数解の和と積を用いた条件に置き換えるのは誤りです。
実数解の和と差を利用できるのは、正負の判断くらいで特定の値との大小関係には向かない。単純に実数解の和と積を用いた条件に置き換えるのは絶対にダメ。
次は、実数解の和と差の正しい利用法を解説します。
２次方程式の実数解の符号問題へと帰着させる
このままだと実数解の和と差を用いた条件に置き換えることができません。しかし、前回の学習内容を利用すればそれが可能になります。「２次方程式の実数解の符号問題へと帰着させる」ことが正しい置き換え方です。
「２次方程式の実数解の符号が正か負か」という話であれば、逆も成り立つので、実数解の和と積を用いた条件で表すことができます。そのために、放物線を平行移動させます。
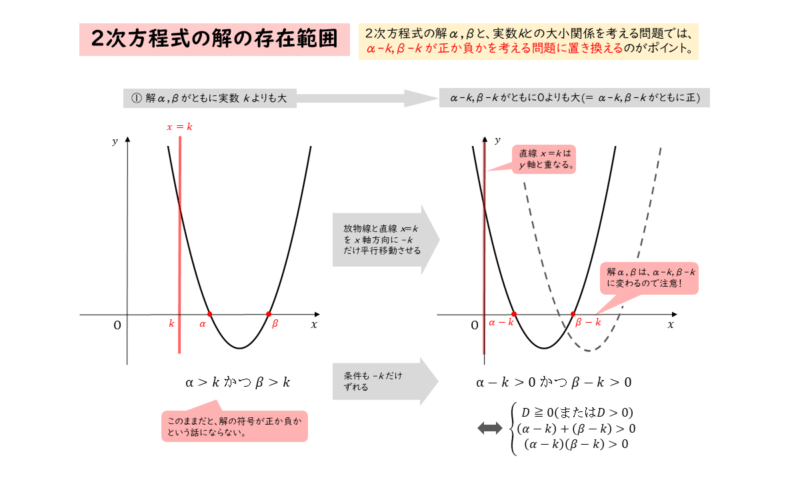２次方程式の実数解の符号問題へと帰着させる たとえば、２つの実数解α，βがともに実数ｋより大きい場合、共有点が直線ｘ＝ｋよりも右側にあります。この直線ｘ＝ｋは、ｘ軸方向に－ｋだけ平行移動させると、ｙ軸に重なります。
このような平行移動の結果、共有点のｘ座標はα－ｋ，β－ｋへと変わります。
放物線を平行移動させることによって、以下のように話を置き換えることができます。
２次方程式の実数解の符号問題への帰着
２つの実数解α，βがともに実数ｋより大きい
⇒ ２つの実数解α－ｋ，β－ｋの符号がともに正
実数解の符号についてであれば、実数解の和と積を用いて条件を導くことができます。ただし、実数解と言っても、平行移動した後の共有点のｘ座標α－ｋ，β－ｋを用いることに注意しましょう。
３通りの場合についてまとめると以下のようになります。
２次方程式の解の存在範囲
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 7pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \quad (\alpha \lt \beta) \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を $D$ とする。} \\[ 5pt ]
&[1] \ \alpha \gt k \ \text{かつ} \ \beta \gt k \\[ 7pt ]
&\quad \alpha-k \gt 0 \ \text{かつ} \ \beta-k \gt 0 \\[ 7pt ]
&\quad \Leftrightarrow \ \begin{cases}
D \geqq 0 \\[ 7pt ]
\left(\alpha-k \right)+\left(\beta-k \right) \gt 0 \\[ 7pt ]
\left(\alpha-k \right) \left(\beta-k \right) \gt 0
\end{cases} \\[ 10pt ]
&[2] \ \alpha \lt k \ \text{かつ} \ \beta \lt k \\[ 7pt ]
&\quad \alpha-k \lt 0 \ \text{かつ} \ \beta-k \lt 0 \\[ 7pt ]
&\quad \Leftrightarrow \ \begin{cases}
D \geqq 0 \\[ 7pt ]
\left(\alpha-k \right)+\left(\beta-k \right) \lt 0 \\[ 7pt ]
\left(\alpha-k \right) \left(\beta-k \right) \gt 0
\end{cases} \\[ 10pt ]
&[3] \ \alpha \lt k \lt \beta \\[ 7pt ]
&\quad \alpha-k \lt 0 \lt \beta-k \\[ 7pt ]
&\quad \Leftrightarrow \ \left(\alpha-k \right) \left(\beta-k \right) \lt 0
\end{align*}
実数解の符号問題へ帰着させず、単純に実数解の和と差を用いる間違いが非常に多いので気を付けましょう。
正しい解法が分かったので、２次方程式の解が存在する範囲を扱った問題を実際に解いてみましょう。
