整数の性質｜ユークリッドの互除法について

08/15/2023数学Ａ

今回は、ユークリッドの互除法について学習しましょう。ユークリッドの互除法も頻出の単元です。

本来の使い方よりも応用的な使い方の方が出題されます。十分に演習をこなしておきましょう。

割り算と最大公約数、ユークリッドの互除法

この単元では、以下のような事柄を学習します。

ユークリッドの互除法の単元で学習する事柄

割り算と最大公約数
ユークリッドの互除法

新しい用語や定理が出てきます。まずは文言通りに正しく覚えることが大切です。

割り算と最大公約数の関係

割り算したときの商や余りを用いて、もとの整数を表せることはすでに学習しました。この単元では最大公約数との関係について学習します。

整数の性質｜最大公約数と最小公倍数について

２数の最大公約数

割り算と最大公約数の間には、一般に、以下の定理が成り立ちます。

割り算と最大公約数

$2$ つの自然数 $a \ , \ b \ (a \gt b)$ について

$a$ を $b$ で割った商を $q$ 、余りを $r$

とすると、 $a$ と $b$ の最大公約数は、 $b$ と $r$ の最大公約数に等しい。

この定理の証明は以下のようになります。証明では、ａとｂの最大公約数ｇがｂとｒの公約数になり、なおかつｂとｒの最大公約数ｇ’がａとｂの公約数になることを示しています。

割り算と最大公約数の定理の証明

自然数 $a$ を自然数 $b$ で割った商 $q$ と余り $r$ を用いると

$\begin{align*} \quad a = bq+r \quad \cdots \text{①} \end{align*}$

これを変形すると

$\begin{align*} \quad r = a – bq \quad \cdots \text{②} \end{align*}$

ここで、 $a$ と $b$ の最大公約数を $g$ とし、 $b$ と $r$ の最大公約数を $g’$ とすると

$\begin{align*} &\quad a = \alpha g \quad \cdots \text{③} \\[ 7pt ] &\quad b = \beta g = \beta’ g’ \quad \cdots \text{④} \\[ 7pt ] &\quad r = \gamma g’ \quad \cdots \text{⑤} \end{align*}$

ただし、 $\alpha$ と $\beta$ 、 $\beta’$ と $\gamma$ はそれぞれ互いに素

②，③，④より

$\begin{align*} \quad r = \alpha g – \beta g q = g(\alpha – \beta q) \end{align*}$

となるので、 $g$ は $r$ の約数である。

これより、 $g$ は $b$ と $r$ の公約数となるので

$\begin{align*} \quad g \leqq g’ \quad \cdots \text{⑥} \end{align*}$

また、①，④，⑤より

$\begin{align*} \quad a = \beta’ g’q + \gamma g’ = g'(\beta’ q + \gamma) \end{align*}$

となるので、 $g’$ は $a$ の約数である。

これより、 $g’$ は $a$ と $b$ の公約数となるので

$\begin{align*} \quad g’ \leqq g \quad \cdots \text{⑦} \end{align*}$

⑥，⑦より $g = g’$ が成り立つ。

したがって、 $a$ と $b$ の最大公約数は、 $b$ と $r$ の最大公約数に等しい。

証明において、ｇ≦ｇ’やｇ’≦ｇとしたのは、その時点では公約数になることは確かでも、それが最大公約数になるとは言い切れないからです。

また、２つの不等式を同時に満たすのは等号が成立するときだけであることから、ｇ＝ｇ’を導出しています。

なお、割り算で成り立つ等式ａ＝ｂｑ＋ｒでは、０≦ｒ＜ｂを満たす整数ｑ，ｒがただ１つに定まりましたが、この定理を適応するときは、必ずしも０≦ｒ＜ｂである必要はありません。

つまり、単にａ＝ｂｑ＋ｒの形に書き表された式に対して、定理が成り立つと考えて良いということです。

必ずしも０≦ｒ＜ｂである必要はない例

$30$ と $4$ の最大公約数を求めるとする。

$\begin{align*} &\quad 30 = 4 \cdot 7 + 2 \\[ 7pt ] &\quad ( b=4 \ , \ r=2 \ \text{に相当} ) \end{align*}$

について、 $4$ と $2$ の最大公約数は $2$ より、 $30$ と $4$ の最大公約数は $2$ 。

また

$\begin{align*} &\quad 30 = \underline{4} \cdot 6 + \underline{6} \\[ 7pt ] &\quad ( b=4 \ , \ r=6 \ \text{に相当} ) \end{align*}$

について、 $4$ と $6$ の最大公約数は $2$ より、 $30$ と $4$ の最大公約数は $2$ 。

したがって、定理が成り立つのに必ずしも $0 \leqq r \lt b$ である必要はない。

以上のことから、割り算と最大公約数の関係について以下のことが成り立ちます。

割り算と最大公約数の関係について成り立つ事柄

$2$ つの自然数 $a \ , \ b \ (a \gt b)$ について、 $a$ を $b$ で割った商を $q$ 、余りを $r$ とする。

$(i) \ r \neq 0$ のとき

$\begin{align*} \quad \text{（$a$ と $b$ の最大公約数）＝（$b$ と $r$ の最大公約数）} \\[ 7pt ] \end{align*}$

$(ii) \ r=0$ のとき

$\begin{align*} \quad \text{（$a$ と $b$ の最大公約数）＝ $b$} \end{align*}$

２つの自然数の最大公約数を求めるとき、２つの自然数が大きければ大きいほど、最大公約数を求めるのは大変になります。

しかし、この定理から、もとの自然数よりも小さな２数の最大公約数を考えれば良いことが分かります。

２数の最大公約数を求める方法として、素因数分解を利用するのが基本だが、この定理を利用して求めることができることも知っておこう。

次は、ユークリッドの互除法についてです。

ユークリッドの互除法

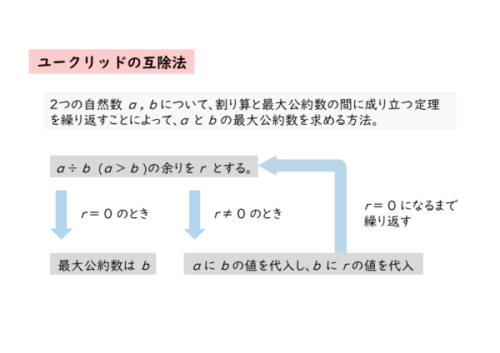
ユークリッドの互除法とは、割り算と最大公約数の間に成り立つ定理を利用して、２つの自然数ａ，ｂの最大公約数を求める方法のことです。

先程の定理を実際に利用する方法と考えると良いでしょう。

ユークリッドの互除法では、ａ，ｂの最大公約数がｂ，ｒの最大公約数に等しくなることを利用して、割り算を繰り返し行います。

ａ÷ｂから余りｒを求めたら、次はｂ÷ｒから余りを求めます。このように余りが０になるまで割り算を繰り返します。

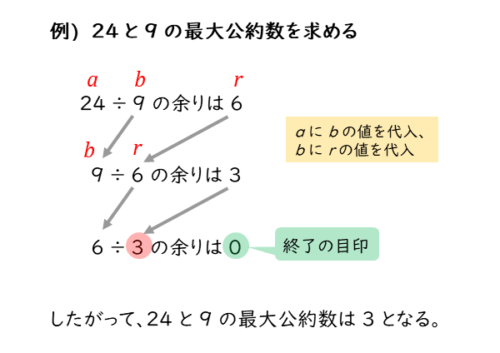
たとえば、２４と９の最大公約数を求めてみましょう。

まず２４÷９を計算します。余りが６になるので、次は９÷６を計算します。余りが３になるので、さらに６÷３を計算します。余りが０になるので、これで割り算を終了します。

余りが０になるときの割る数（除数）３が２４と９の最大公約数になります。

この計算で分かるのは、最大公約数を求めるために、２４と９から直接求めるのではなく、できるだけ小さな２つの自然数（ここでは６と３）に置き換えて間接的に求めているということです。

これは割り算と最大公約数の間に成り立つ定理があるからできることです。

２４と９の最大公約数は、６と３の最大公約数を求めれば良い。

（２４と９の最大公約数）

＝（９と６の最大公約数）

＝（６と３の最大公約数）

難しく感じるかもしれませんが、式を書いていくと２つの数が横にスライドするだけだと分かります。ですから、要領さえ掴んでしまえば、あとは機械的に計算できるようになります。

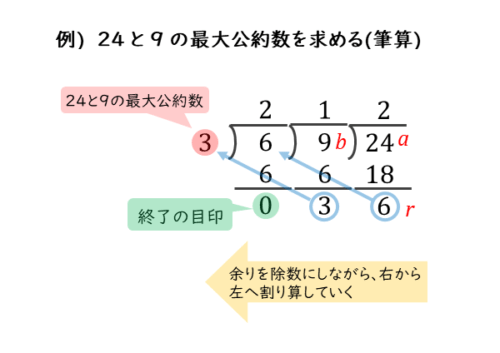
また、実際に筆算して解くこともできます。後で学習する不定方程式には使いにくいですが、単に最大公約数を求めるだけなら筆算の方が解きやすいでしょう。

２４÷９を計算して余りを求めます。

余り６で９を割るので、９の左側に６を書き、９÷６の余りを求めます。

余り３で６を割るので、６の左側に３を書き、６÷３の余りを求めます。

余りが０になるので、このときの割る数（除数）３が２４と９の最大公約数になります。

この筆算では、余りが次の割り算の割る数（除数）になるので、左側へ除数を追記していきながら割り算します。

例では２つの自然数がわりと小さな数でしたが、実際はもっと大きな数を扱うので、筆算での求め方をマスターしておいた方が良いでしょう。

次は、ユークリッドの互除法を扱った問題を実際に解いてみましょう。

数学Ａ余り,最大公約数,除数,整数の性質,ユークリッドの互除法

Posted by kiri