整数の性質｜ユークリッドの互除法について

08/15/2023数学Ａ

ユークリッドの互除法を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

$270$ と $42$ の最大公約数をユークリッドの互除法を用いて求めよ。

問の解答・解説

最大公約数の求め方には、２つの数をそれぞれ素因数分解して求める方法があります。この方法はすでに学習しています。しかし、問では解法が指定されているので注意しましょう。

素因数分解せずに、ユークリッドの互除法を用いて解きます。

問の解答例

\begin{align*} &\quad 270 \div \underline{42} = 6 \quad \text{余り} \ \underline{\underline{18}} \\[ 7pt ] &\quad \underline{42} \div \underline{\underline{18}} = 2 \quad \text{余り} \ \underline{6} \\[ 7pt ] &\quad \underline{\underline{18}} \div \underline{6} = 3 \quad \text{余り} \ \underline{\underline{0}} \end{align*}

よって、$270$ と $42$ の最大公約数は $6$

割る数（除数）を次の割り算の割られる数（被除数）に、余りを次の割り算の割る数（除数）にして割り算を繰り返します。余りが０になったときの割る数（除数）が２７０と４２の最大公約数です。

解答例から分かるように、２７０と４２の最大公約数を直接求めるのではなく、１８と６の最大公約数から間接的に求めています。

２７０と４２の最大公約数は、１８と６の最大公約数を求めれば良い。

（２７０と４２の最大公約数）

＝（４２と１８の最大公約数）

＝（１８と６の最大公約数）

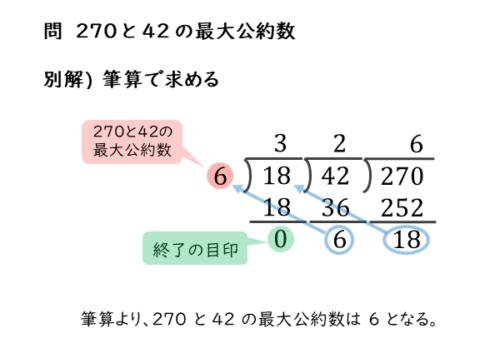
また、筆算で解くと以下のようになります。

余りが次の割り算の割る数（除数）となります。

左側に追記していくので、最初の割り算をできるだけ右側に記述しましょう。

数題解けば要領を掴めるので、集中的に演習をこなしましょう。

ユークリッドの互除法を扱った問題の別解例 — ２７０と４２の最大公約数を筆算で求める

最大公約数の求め方としては、素因数分解を利用する解法が一般的かもしれません。ただ、整数問題では余りに注目する問題が意外と多いので、余りに関わる解法の１つとしてユークリッドの互除法も使えるようにしておきましょう。

発展の内容になりますが、余りに注目したものに合同式もあります。

Recommended books

整数の性質を扱った問題は、難関大なら必修でしたが、センター試験でも扱われるようになりました。

難しく感じる人もいるかもしれませんが、複雑な公式や図形を扱うことがないので、その気になれば得点源にできる単元です。単元別の問題集で集中的に取り組んでマスターしましょう。

これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。

オススメその１

『２週間で完成！整数問題入試対策編』は、教科書レベルから始めて大学入試の実戦レベルまで、最大効率で習得できる問題集です。新課程の整数問題に対応しています。問題数が４７題なので、短期間でこなしたいなら候補に入れて良いでしょう。

【教科書編】
問題数１６題。新課程版教科書「整数の性質」の項目に沿って配置。
教科書編項目:約数と倍数/約数の個数と総和/最大公約数と最小公倍数/剰余による分類/ユークリッドの互除法とディオファントス方程式/ｐ進法/循環小数/合同式/部屋割り論法

【実戦問題のレベル別編】
初級編２０題、中級編５題、上級編６題。
難関大学の整数問題に十分対処できるようにすることを目標として作成。
できる限り数学１・数学Ａの範囲にとどめるように問題を選択。
ただし、二項定理・高次の多項式の因数分解・数列の問題あり。

数学１・Ａの範囲内にとどめるように配慮されているおかげで、数学１・Ａの学習直後から取り組めます。学習したてなら苦手意識がつく前なので、スムーズに取り組めるでしょう。

２週間で完成！整数問題入試対策編

created by Rinker

オススメその２

『教科書だけでは足りない大学入試攻略整数』では、入試の整数問題１０００題から選ばれた問題が収録されています。例題、類題、力試し問題と３ステップで進めていけるので、自分の学力に合わせて周回できます。解答例や解説は、高校までに学んだ知識だけで理解できるように配慮されているので、数学が苦手な人にも取り組みやすくなっています。

整数問題は、難関大入試では頻出で、しかも教科書の問題と入試とではそのレベルの差が激しい分野のひとつです。また、経験値がものをいう問題が多いことも確かです。そこで、ここ数十年の大学入試の整数問題約１０００題の中からぜひやっておきたい問題を例題、類題、力だめし問題として計８１題セレクトしました。

高校までに学んだ知識だけで理解できる解説、解答例を作成しています。

定石を身に付けつつ、入試を想定した問題を解いてみたいのなら候補に入れて良いでしょう。