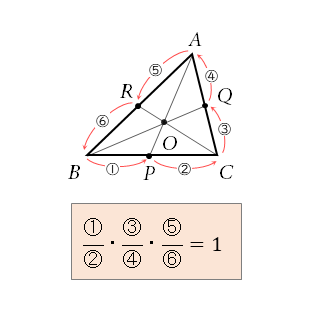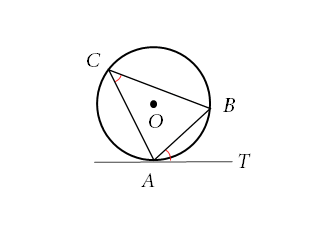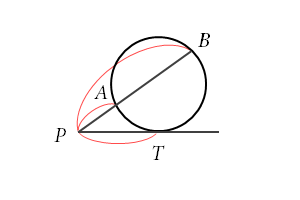数学の公式・定理集｜図形の性質
目次
図形の性質
三角形の辺の比、外心・内心・重心
三角形の角の二等分線と比
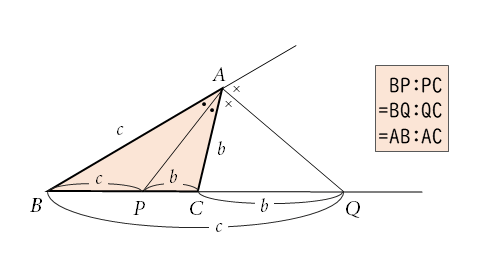
- △ABC の∠A の二等分線と辺 BC との交点 P は、辺 BC を AB：AC に内分する。
- AB≠AC である△ABC の∠A の外角の二等分線と辺 BC の延長との交点 Q は、辺 BC を AB：AC に外分する。
関連記事
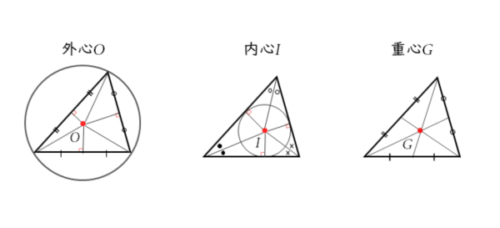
外心・内心・重心
- 外心：３辺の垂直二等分線の交点。
- 内心：３つの内角の二等分線の交点。
- 重心：３つの中線の交点。重心は各中線を 2：1 に内分する。
垂心
三角形の各頂点から対辺またはその延長に下ろした垂線の交点。
チェバの定理、メネラウスの定理
チェバの定理
△ABC の頂点 A, B, C と辺上にもその延長上にもない点 O を結ぶ各直線が、対辺またはその延長とそれぞれ P, Q, R で交わるとき
\begin{equation*}
\quad \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB} =1
\end{equation*}
メネラウスの定理
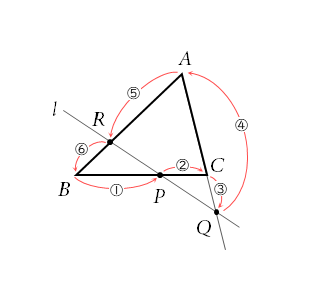
△ABC の辺 BC, CA, AB またはその延長が頂点を通らない直線ℓと、それぞれ点 P, Q, R で交わるとき
\begin{equation*}
\quad \frac{BP}{PC} \cdot \frac{CQ}{QA} \cdot \frac{AR}{RB} =1
\end{equation*}
三角形の３辺の長さの性質
三角形の３辺の長さを a, b, c とすると
\begin{equation*}
\quad b-c \lt a \lt b+c
\end{equation*}
これを三角形の成立条件と言う。
円周角、円に内接する四角形
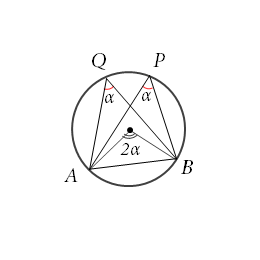
円周角の定理とその逆
図参照
４点 A, B, C, D が１つの円周上にある
⇔ ∠APB = ∠AQB
関連記事
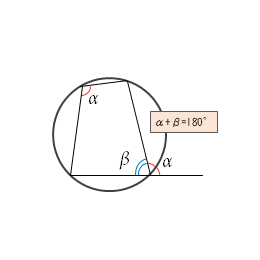
円に内接する四角形
四角形が円に内接するとき、以下のことが成り立つ。
- 対角の和は 180°
- 内角は、その対角の外角に等しい。
逆に、１または２が成り立つ四角形は、円に内接する。
関連記事
円と直線、方べきの定理
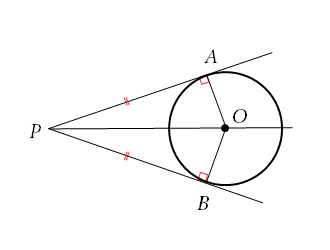
円の接線
図参照
円外の点 P から接線 PA, PB を引く。ただし、点 A, B は接点。
このとき以下のことが成り立つ。
- OA⊥PA
- OB⊥PB
- PA = PB
関連記事
接弦定理とその逆
図参照
直線 AT が円 O の接線
⇔ ∠ACB = ∠BAT
関連記事
方べきの定理
図１
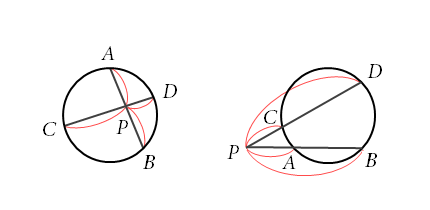
図１参照
(1) 円の２つの弦 AB, CD またはそれらの延長の交点を P とすると
\begin{equation*}
\quad PA \cdot PB = PC \cdot PD
\end{equation*}
図２
図２参照
(2) 円の外部の点 P から円に引いた接線の接点を T とし、P を通りこの円と２点 A, B で交わる直線を引くと
\begin{equation*}
\quad PA \cdot PB = {PT}^{2}
\end{equation*}
関連記事
方べきの定理の逆
２つの線分 AB と CD、または AB の延長と CD の延長が点 P で交わるとき、
\begin{equation*}
\quad PA \cdot PB = PC \cdot PD
\end{equation*}
が成り立つならば、４点 A, B, C, D は１つの円周上にある。
三垂線の定理
平面α上に直線ℓがあるとき、α上にない点 A、ℓ上の点 B、ℓ上にないα上の点 O について
AB⊥ℓ, OB⊥ℓ, OA⊥OB ならば、OA⊥α
直線と平面、多面体
空間における直線や平面の位置関係
- 平行な２直線の一方に垂直な直線は、他方にも垂直である。
- 直線ℓが、平面α上の交わる２直線 m, n に垂直ならば、直線ℓは平面αに垂直である。
- 平面αの１つの垂線を含む平面は、αに垂直である。
多面体
以下の２つの条件を満たす凸多面体を正多面体と言う。
- 各面はすべて合同な正多角形である。
- 各頂点に集まる面の数はすべて等しい。
関連記事
オイラーの多面体定理
凸多面体の頂点の数を v、辺の数を e、面の数を f とすると
\begin{equation*}
\quad v-e+f=2
\end{equation*}
おすすめの数学辞典
公式や定理をまとめた数学辞典です。１冊あると便利です。
おすすめ その1
導出が丁寧に記載されている公式集を１冊もっておくと困ったときに辞書代わりになります。 ポケットサイズのものと違いサイズが少し大きいので、図が豊富です。
おすすめ その2
公式・定理・定義は左ページ、活用例・解説・証明は右ページの見開き構成になっているので、使いやすいです。
おすすめ その3
難関大を志望している人向けです。大学に進学してからも使えます。
