２次関数｜２次関数のグラフとx軸との位置関係について

04/10/2022数学１

今回は２次関数のグラフとｘ軸との位置関係について学習しましょう。

今回の内容を学習すれば、２次方程式の解が２次関数のグラフとどのように関係するのかを知ることができます。

また、２次不等式の解を求めるには、２次方程式と２次関数の知識を必要とします。

特に、２次不等式を解くために、２次方程式を解いたり、２次関数のグラフを用いたりするので互いの関係を理解しておく必要があります。

グラフとｘ軸との位置関係は３パターン

２次方程式の解のことや、その判別の方法を学習しました。これらの知識を利用すると、グラフとｘ軸との位置関係を知ることができます。

グラフとｘ軸との位置関係は、グラフとｘ軸との交点を調べることで分かります。交点の個数は３パターンあります。

それぞれの場合になるには、どのような条件が必要なのかを考えてみましょう。

２次関数の式と２次方程式との関係

２次関数の式と２次方程式との関係を考えてみましょう。

２次関数は変数ｙが変数ｘの２次式で表される式です。２つの変数ｘ，ｙの関係を表すのが関数です。

この２次関数の式において、ｙ＝０のときの式が変数ｘについての２次方程式です。

つまり、２次方程式は２次関数の式から得られる式の１つということです。

２次関数のグラフと２次方程式の解との関係

２次関数において、ｙ＝０のときの式が２次方程式です。この２次方程式を解くと、解を得ることができます。

この解は２次関数とどのような関係があるのでしょうか？

２次方程式の解は、２次関数ではｙ＝０のときの変数ｘの値です。この変数ｘの値は、２次関数のグラフで考えると、グラフ上、かつｘ軸上にある点、つまりグラフとｘ軸との交点のｘ座標です。

特に、解が実数解であればｙ＝０のときの変数ｘの値が実数の範囲で存在することを意味します。

ｙ＝０のときの変数ｘの値は、グラフ上、かつｘ軸上の点のｘ座標を表します。このような点のｘ座標が得られることから、グラフがｘ軸と交点をもつように可視化することができます。

ちなみに、交点のことを共有点と言います。グラフとｘ軸が同じ点を共有しているからです（以下、交点のことを共有点と言う）。

２次方程式の実数解に応じて、ｘ軸と共有点をもつかどうかを判別できます。また、実数解の個数に応じて、共有点の個数も判別できます。

実数解の有無や個数は、２次方程式の解の判別式によって判別できます。ここで、実数解と共有点とは連動していることが分かっています。ですから、共有点の有無や個数も２次方程式の解の判別式によって判別できることが分かります。

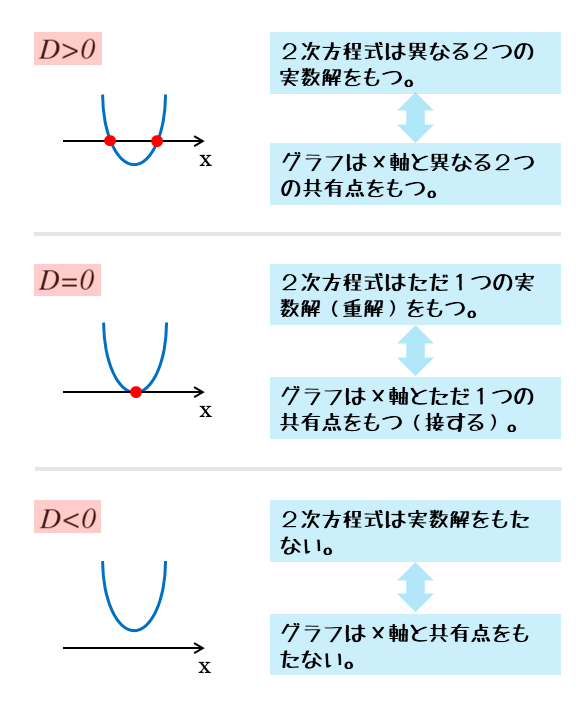
たとえば、２次方程式の判別式Ｄの値がＤ＞０であれば、２次方程式は異なる２つの実数解をもちます。

この実数解は共有点のｘ座標のことです。ｘ座標が２つ得られるということは、グラフとｘ軸との共有点が２個できるということです。

このように、判別式は、実数解の個数だけでなく、共有点の個数も教えてくれます。共有点の個数が分かれば、ｘ軸に対するグラフの位置も分かるので、作図に利用できるようになります。

２次関数のグラフとｘ軸との位置関係

２次関数のグラフとｘ軸との位置関係は、判別式の値によって場合分けできます。２次方程式の実数解の個数が共有点の個数に等しいからです。

位置関係は凸の向きに関わらず３パターンです。

式や言葉だけでなく、グラフとセットで覚えることが大切です。

注意したいのは、２次方程式が重解をもつときです。

グラフとx軸との位置関係は「接する」という言葉で表現します。

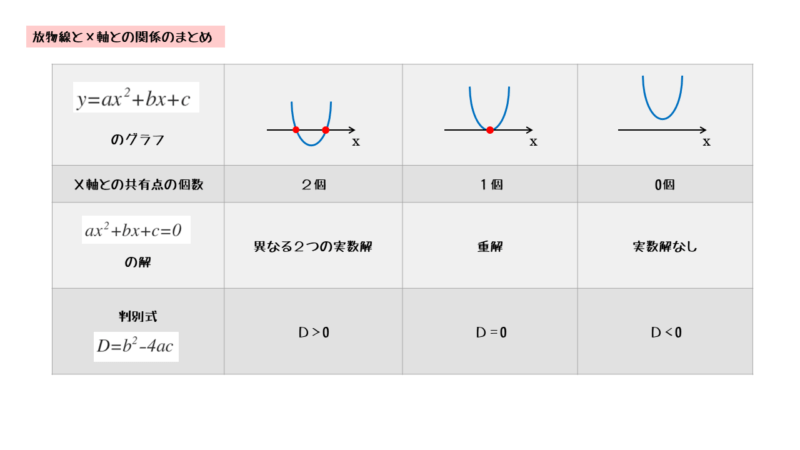
一覧表にすると以下のようになります。図表を活用して、２次関数・２次方程式・グラフの関係を把握しましょう。

実数解の個数と判別式との関係はもちろんですが、グラフとｘ軸との位置関係も併せて覚えることが大切です。

次は、グラフとｘ軸との位置関係を扱った問題を解いて、理解度を確かめてみましょう。