2次関数|2次不等式の解法について(基本編)

2次不等式の解法・基本編
2次不等式の解を求める詳しい手順は上述の通りです。ただ、実際には、左辺の2次式に応じて、簡略化した解き方をする場合があります。
共有点のx座標を求めるときに注目して解法をパターン化してみます。
2次方程式の解法は、グラフとx軸との共有点の有無で異なります。今回は、基本編として、共有点が2つ存在する、すなわち2次方程式が異なる2つの実数解をもつときの解法です。
共有点のx座標は、2次関数においてy=0のときの2次方程式を解くことで得られます。2次方程式の解法は2パターンです。
2次方程式の解法は2パターン
- 2次方程式を因数分解して解く
- 2次方程式を解の公式で解く
2次方程式をどちらで解くかによって、2次不等式の解の求め方が変わってきます。
基本編・2次不等式の左辺を因数分解できるとき
先ほどの例で考えてみましょう。2次方程式を因数分解したところから逆に辿ってみましょう。
2次不等式・2次方程式の左辺、2次関数の右辺に注目する
\begin{align*} \quad &\underline{{x}^{2}-2x-3} \lt 0 \\[ 7pt ] &\quad \vdots \\[ 7pt ] \quad &y=\underline{{x}^{2}-2x-3} \quad \left( y \lt 0 \right) \\[ 7pt ] &\quad \vdots \\[ 7pt ] \quad &\underline{{x}^{2}-2x-3} = 0 \end{align*}これを解くと
\begin{align*} \quad {x}^{2}-2x-3 &= 0 \\[ 7pt ] \left( x+1 \right)\left( x-3 \right) &= 0 \\[ 7pt ] \therefore \ x &= -1 \ , \ 3 \end{align*}よって、$y \lt0 $ を満たすのは
\begin{align*} \quad -1 \lt x \lt 3 \end{align*}2次不等式と2次方程式の左辺、2次関数の右辺の3つはともに同じ式です。ということは、2次関数の右辺と2次不等式の左辺も、2次方程式の左辺と同じ形に因数分解できるはずです。
このような場合、2次不等式の左辺を因数分解して、2次不等式の解を一気に求めてしまいます。ですから、2次関数や2次方程式のことを記述しません。
2次関数・2次方程式なしで2次不等式を解く
\begin{align*} \quad \underline{{x}^{2}-2x-3} &\lt 0 \\[ 7pt ] \quad \left( x+1 \right)\left( x-3 \right) &\lt 0 \\[ 7pt ] \therefore \ -1 \lt x \lt 3 \end{align*}本来ならば、2次関数や2次方程式を利用して2次不等式の解を求めます。
しかし、2次不等式の左辺を因数分解できる場合、2次不等式の解に必要な共有点のx座標が分かってしまうので、途中を省略できるのです。
2次不等式の左辺を因数分解できると共有点のx座標が分かる
(2次不等式の左辺を因数分解できた)=(2次方程式の解を求める直前の式になった)
一般に、2次不等式の左辺を因数分解できるときの解は以下のように表せます。
2次不等式の解法 1⃣
\begin{align*} \quad a{x}^{2}+bx+c \lt 0 \quad ( a \gt 0 \ , \ \alpha \lt \beta ) \end{align*}が以下のように変形できるとき
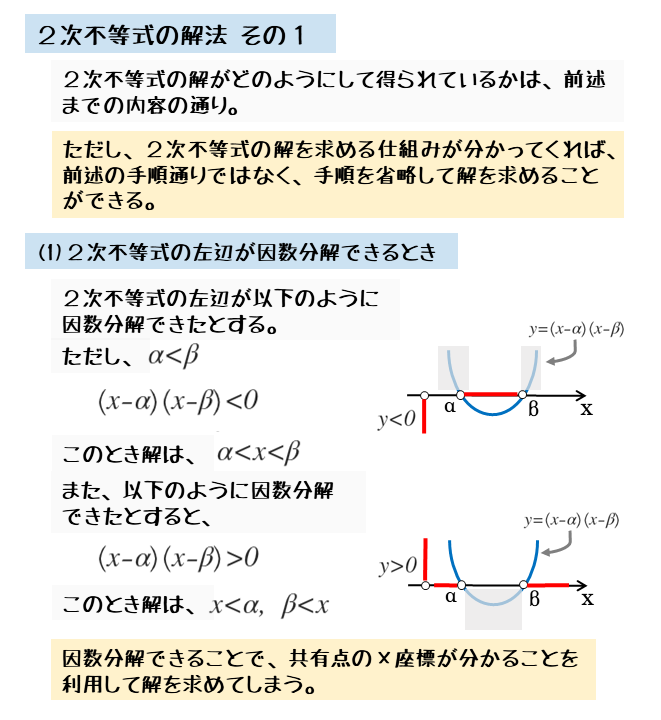
\begin{align*} \quad a \left( x- \alpha \right) \left( x- \beta \right) \lt 0 \end{align*}$2$ 次不等式の解は
\begin{align*} \quad \alpha \lt x \lt \beta \end{align*}また
\begin{align*} \quad a{x}^{2}+bx+c \gt 0 \quad ( a \gt 0 \ , \ \alpha \lt \beta ) \end{align*}が以下のように変形できるとき
\begin{align*} \quad a \left( x- \alpha \right) \left( x- \beta \right) \gt 0 \end{align*}$2$ 次不等式の解は
\begin{align*} \quad x \lt \alpha \ , \ \beta \lt x \end{align*}このように一般化されているので、上述の条件に当てはまれば2次不等式の解を簡単に求めることができます。
しかし、2次関数や2次方程式との関係を理解するために、グラフを描いて解を求める習慣を付けておいた方が無難です。
2次不等式の左辺を因数分解できるときが一番易しい問題。
基本編・2次不等式の左辺を因数分解できないとき
2次不等式の左辺を因数分解できないとき、左辺を変形できません。ですから、このままでは共有点のx座標が分からないので、2次方程式を導出してから解きます。
2次不等式の左辺を因数分解できないとき
\begin{align*} \quad {x}^{2}-2x-1 \lt 0 \end{align*}より
\begin{align*} \quad y = {x}^{2}-2x-1 \quad \left( y \lt 0 \right) \end{align*}ここで、$y=0$ のとき
\begin{align*} \quad {x}^{2}-2x-1 = 0 \end{align*}解の公式より
\begin{align*} \quad x &=\frac{-\left(-1 \right) \pm \sqrt{\left( -1 \right)^{2}- 1 \cdot (-1)}}{1} \\[ 7pt ] &=1 \pm \sqrt{2} \end{align*}よって、$y \lt 0$ を満たすのは
\begin{align*} \quad 1-\sqrt{2} \lt x \lt 1+\sqrt{2} \end{align*}関数化の話を省略すると以下のようになります。
関数化を省略して解く
\begin{align*} \quad {x}^{2}-2x-1 \lt 0 \end{align*}与式より
\begin{align*} \quad {x}^{2}-2x-1 = 0 \end{align*}とおくと、解の公式より
\begin{align*} \quad x &=\frac{-\left(-1 \right) \pm \sqrt{\left( -1 \right)^{2}- 1 \cdot (-1)}}{1} \\[ 7pt ] &=1 \pm \sqrt{2} \end{align*}2次方程式の解を求めたら、因数分解できるときと同じように不等式の解を求めます。2次不等式の不等号を見て、向きに対応する解の形に合わせます。
一般に、左辺をもとにした2次方程式の解は、2次不等式の解と以下のような関係があります。
2次方程式の解と2次不等式の解との関係
$2$ 次方程式
\begin{align*} \quad ax^{2}+bx+c = 0 \quad \left(a \gt 0 \right) \end{align*}が異なる $2$ つの実数解 $\alpha \ , \ \beta \ (\alpha \lt \beta)$ をもつとき
\begin{align*} \quad a\left(x-\alpha \right)\left(x-\beta \right) \lt 0 \end{align*}の解は
\begin{align*} \quad \alpha \lt x \lt \beta \end{align*}また
\begin{align*} \quad a\left(x-\alpha \right)\left(x-\beta \right) \gt 0 \end{align*}の解は
\begin{align*} \quad x \lt \alpha \ , \ x \lt \beta \end{align*}2次方程式と2次不等式との解の関係を参考すると、2次不等式の解を求めることができます。
不等号を見て解を求める
\begin{align*} \quad {x}^{2}-2x-1 \lt 0 \end{align*} \begin{align*} \quad \vdots \end{align*} \begin{align*} \quad x &=\frac{-\left(-1 \right) \pm \sqrt{\left( -1 \right)^{2}- 1 \cdot (-1)}}{1} \\[ 7pt ] &=1 \pm \sqrt{2} \end{align*}よって、$2$ 次不等式の解は
\begin{align*} \quad 1-\sqrt{2} \lt x \lt 1+\sqrt{2} \end{align*}不等式の左辺を因数分解できないとき、注意したいのは2次不等式のままで解の公式を使ってしまうことです。解の公式は、2次方程式の解を求めるための式であって、2次不等式を解くための公式ではないからです。
同じ結果が得られたとしても、間違った過程や使い方にならないように気を付けましょう。
また、2次不等式の左辺を因数分解できる、できないにかかわらず、左辺を用いた2次方程式の解が分かれば、以下の関係を利用します。
もちろんグラフも利用しますが、最終的にはこの解法を用いて、2次不等式の解を求めることになります。
2次不等式を解くときの注意点
2次不等式の左辺を因数分解できるできないに関わらず、注意したいことが2つあります。
1つ目は、2次の項の係数が正の数であることです。
2次不等式を解くとき、2次の項の係数が正の数であることを前提にして解きます。このことはグラフを利用するときに役立ちます。
2次の項の係数が正の数であれば、グラフの向きは下に凸になります。つまり、いつも同じ向きのグラフを用いて考えることができます。図示するときに迷わなくて済みます。
2つ目は、不等式の右辺が必ず0であることです。
右辺が0であれば、2次関数に置き換えたときの値域が0より大きいや小さいなどの不等式になります。
このような値域に対応するグラフは、いつもx軸に対して上または下のどちらかになります。また、共有点のx座標も定義域に使えるようになります。
2次不等式を解く前にチェック!
- 2次の項の係数は正の数になっているか
- 2次不等式の右辺は0になっているか
次は、2次不等式を扱った問題を実際に解いてみましょう。