場合の数|円順列、重複順列について

今回は円順列や重複順列について学習しましょう。どのような場合に円順列や重複順列になるのかをしっかり覚えましょう。
記事の画像が見辛いときはクリックすると拡大できます。
円順列、重複順列の定義
円順列とは、いくつかの異なるものを円形に並べる順列のことです。たとえば、複数の人が円形のテーブルに沿って座る場合が円順列です。
一般に、円順列の総数は以下のように定義されています。
円順列の総数
異なる $n$ 個のものを円形に並べるとする。
このときの円順列の総数は $(n-1)!$ 通り
また、重複順列とは、いくつかの異なるものから、同じものを何度も取って良いとして、何個か取って並べる順列のことです。たとえば、1~5の数から重複を許して3桁の整数を作る場合が重複順列です。
一般に、重複順列の総数は以下のように定義されています。
重複順列の総数
異なる $n$ 個のものから重複を許して $r$ 個取って並べるとする。
このときの重複順列の総数は $n^r$ 通り
円順列の総数の数え方
円順列の総数は(n-1)!と表されますが、その式を導出してみましょう。導出することで、円順列のことをより理解できるはずです。
円順列も順列の1つ
具体例として、4人が円形のテーブルに沿って座る場合を考えます。このときの座り方は全部で何通りあるでしょうか。
4人をA,B,C,Dとします。
また、円形のテーブルを時計に見立てて、12時の位置から反時計回りに9時、6時、3時の位置に座る場合を考えます。
便宜上、12時の位置を最初に座る席とします。
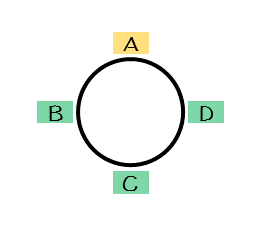
4人は12時の位置から順に並ぶように座っていくので、順列の考え方で場合の数を求めることができそうです。
4人の座り方
- 12時の位置 … 最初の席なので、座り方は4通り
- 9時の位置 … 12時の位置の座り方のそれぞれについて、3人残っているので3通りずつ
- 6時の位置 … 9時の位置の座り方のそれぞれについて、2人残っているので2通りずつ
- 3時の位置 … 6時の位置の座り方のそれぞれについて、1人残っているので1通りずつ
積の法則が成り立つことが分かるので、4人の座り方は4×3×2×1、つまり4!通りになります。
円順列での同じ並びに注意
4人の座り方は4!通りになりましたが、このままだと一列に並んだときの順列の総数です。どこを考慮しないといけないかと言うと「12時の位置から反時計回りに座る」という条件です。
便宜上、最初に座る位置を12時の位置にしましたが、座ってしまえばどの席から順に座っていったのか分かりません。一列ではなく、円形に並ぶからです。
座った結果だけに注目してみると、隣りの組合せが全く同じ座り方が存在することに気付きます。
たとえば、A,B,C,Dの順に並んでいる座り方は4通りあります。
重複する4人の座り方
- 12時の位置から反時計回りにA,B,C,Dが座る場合
- 9時の位置から反時計回りにA,B,C,Dが座る場合
- 6時の位置から反時計回りにA,B,C,Dが座る場合
- 3時の位置から反時計回りにA,B,C,Dが座る場合
これらの並びは、12時の位置に座る人が変わっていますが、両隣りの人が全く変わっていません。
つまり、4人の座る位置がずれただけで、並び方が変わっていないので、このような座り方は円順列では同じ並びとして扱います。
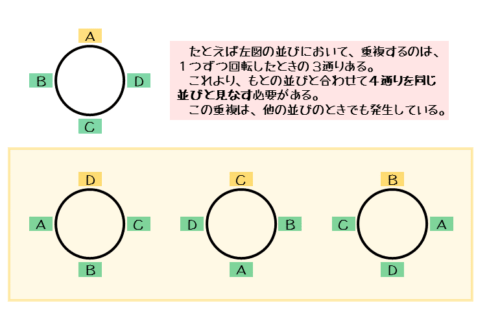
このとき「A,B,C,D」の並びと同じ座り方と見なせるのは、「D,A,B,C」「C,D,A,B」「B,C,D,A」の並びです。これより、「A,B,C,D」の並びは全部で4通りあるので、重複を除くためにこれらを1通りと見なす必要があります。
このことは他の並びにも言えることで、4人を一列に並べたときの樹形図で調べてみると面白いことが分かります。
樹形図で重複ぶんを調べてみよう
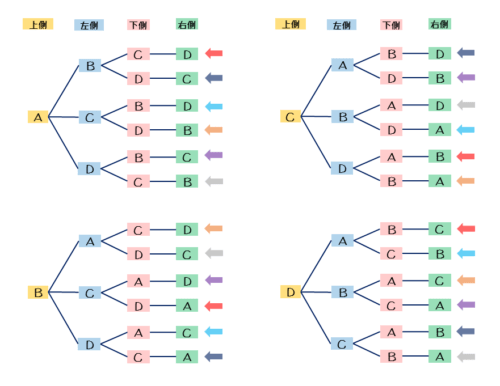
樹形図を書いた後、同じ並びと見なせるものを調べてみます。
同じ並びと見なせるものには印を付けていきます(図では同色の矢印)。すると、12時の位置にAが座るときの並び方のすべてについて、同じ並びと見なせるものが他の樹に必ず1つずつ存在しています。
つまり、同じ並びと見なせるものは1つの並びについて必ず4通りずつあることが分かります。この結果をもとに、12時の位置にAが座るときの並びと重複するものを、他の樹から取り除くとどうなるでしょうか。
重複するものを取り除くと、12時の位置にAが座るときの並び以外の樹はすべてなくなってしまいます。結局、残ったのは12時の位置にAが座るときの並びの樹が1つだけです。
順列の総数から重複ぶんを取り除く
12時の位置に座る座り方を4通りと考えましたが、樹形図の結果から実質1通りで良いということになります。
順列の考え方では4×3×2×1=4!通りと求めましたが、この中から同じ並びと見なせる重複ぶんを取り除く必要があります。重複の原因は最初の数4です。
「4通りのそれぞれについて」の部分を「1通りのそれぞれについて」と修正します。式では以下のように操作することで修正できます。
順列の総数から重複ぶんを取り除く
$4$ 人の並び方は
\begin{align*} \quad 4 \times 3 \times 2 \times 1 \ (=4!) \ \text{(通り)} \end{align*}ただし、$4$ 人を円形に並べるとき、$1$ つの並び方に対して $4$ 通りずつ重複するので
\begin{align*} \quad \frac{4 \times 3 \times 2 \times 1}{4} &= 3 \times 2 \times 1 \\[ 7pt ] &= 3! \end{align*}重複ぶんを取り除くと言うと「重複ぶんを引く⇒減算」というイメージがありますが、減算ではないことに注意しましょう。
n人の場合でも、4人の場合と同じように考えます。1つの並びについて重複ぶんがn通りずつできるので、n!通りの中から重複ぶんを取り除きます。
「n通りのそれぞれについて」の部分を「1通りのそれぞれについて」と修正すれば良いので、円順列の総数を以下のようにして導出できます。
円順列の総数の導出
$n$ 人を円形に並べる円順列の総数は
\begin{align*} \quad \frac{n!}{n} &= \frac{n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot 1}{n} \\[ 10pt ] &= (n-1) \cdot (n-2) \cdot \cdots \cdot 1 \\[ 10pt ] &= (n-1)! \end{align*}円順列の総数とその考え方をまとめると以下のようになります。
円順列の総数は特定のものに対する順列の総数
先ほどの樹形図では、重複ぶんを取り除くと12時の位置にAが座るときだけの樹が残りました。このことはAの場合でなくても同じで、重複ぶんを取り除くと樹は1つだけになります。
このことから分かるのは、特定の1人に対する残りの順列の総数を考えれば、円順列の総数を求めることができるということです。この考え方は意外と大切です。円順列を一列に並べる順列に置き換えることができるからです。
このような「特定の1人(1つ)に対する残りの並びを考える」という考え方は、たとえば色の塗り分けなどで使われます。これを機会に覚えておくと良いでしょう。
円順列の総数は、特定の1人(1つ)に対する残りの順列の総数に等しい。
次は重複順列についてです。
重複順列の総数の数え方
重複順列では、重複を許して並べることができます。たとえば、2つの数から重複を許して3桁の数を作る場合を考えます。
各位の数の選び方は以下のようになります。
2つの数から重複を許して3桁の数の作り方
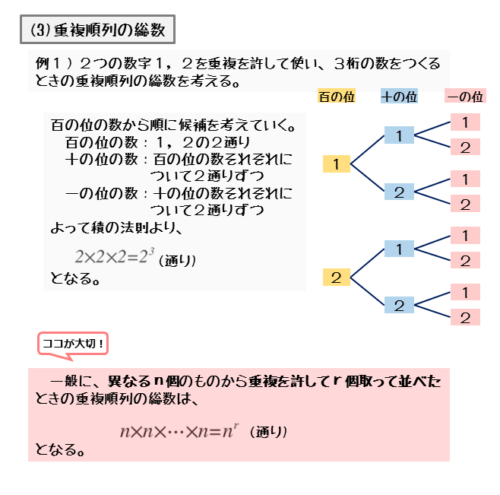
- 百の位 … 2つの数から選ぶので2通り
- 十の位 … 百の位の数のそれぞれについて、2つの数から選ぶので2通りずつ
- 一の位 … 十の位の数のそれぞれについて、2つの数から選ぶので2通りずつ
積の法則が成り立つことが分かるので、3桁の数の作り方は2×2×2=23通りになります。このことは異なるn個のものから重複を許す場合でも成り立ちます。
異なるn個のものから重複を許してr個取って並べた重複順列の総数は、nをr個掛けたnr(通り)となります。
重複順列は円順列に比べると考え方が分かりやすいので、順列の考え方が身に付いていれば、総数を簡単に求めることができます。
次は円順列や重複順列を扱った問題を実際に解いてみましょう。