場合の数|同じものを含む順列について

今回は、同じものを含む順列について学習しましょう。
同じものを含む順列は重複順列に似ているので、よく勘違いする人がいます。両者の違いをしっかり理解しましょう。
記事の画像が見辛いときはクリックすると拡大できます。
重複順列と同じものを含む順列との違いを知ろう
重複順列は、重複を許すという条件で、異なるn個のものからr個取って並べた順列のことです。ですから、並べるものを選ぶことができ、また選んだものが他のものと重複しても許されます。
それに対して、同じものを含む順列は、並べるものの中に同じ種類のものが混じった状態で、それらを並べた順列です。
たとえば、「1,1,5の3つの数を使ってできる3桁の整数の個数」は、重複順列の総数ではありません。この個数は、同じものを含む順列の総数になります。
例からも分かるように、並べるものがすでに決まっています。並べるものを自分で選ぶことはできません。選ばれたものの並べ替えと考えると良いでしょう。
このように重複順列と同じものを含む順列とは全く異なります。定義を正しく覚え、その意味を正しく理解しましょう。
同じものを含む順列の総数を求めよう
n個の中にいくつかの種類があって、それぞれp個、q個、r個、……ずつあるとします。これらn個のものを一列に並べる順列が同じものを含む順列です。
ところで、n個を並べる順列の総数は以下のように表されます。
n個を並べる順列の総数
\begin{align*} \quad n! \text{(通り)} \end{align*}n個のものを並べる順列の総数はn!通りですが、これはn個のものがすべて異なるときの総数です。
もし、n個の中に同じものがp個、q個、r個、……ずつ含まれているとすればどうなるでしょうか。この場合、順列の総数n!通りの中には、重複する並べ方が含まれています。
たとえば、p個が同じものであれば、p個の並べ方p!通りを重複して数え上げていることになります。
同じ種類ごとに重複する並べ方を求め、その重複ぶんを1通りにしなければなりません。この重複ぶんの扱いさえ忘れなければ、同じものを含む順列の総数を簡単に求めることができます。
一般に、n個の中に同じものがp個、q個、r個、……ずつあるとき、その並べ方の総数は以下のように表されます。
同じものを含む順列の総数
$n$ 個の中に同じものが $p$ 個、$q$ 個、$r$ 個、……ずつあるとき、その並べ方の総数は
\begin{align*} \quad \frac{n!}{p! \ q! \ r! \cdots} \text{(通り)} \end{align*}ただし
\begin{align*} \quad p + q + r + \cdots = n \end{align*}また、同じものを含む場合、順列の総数を数え上げてしまうと、同じものの並べ替えが重複することになります。ですから、並べるというよりも置く場所を選ぶと捉えた方が良いでしょう。
「p個(またはq個、r個)のものを置く場所を選ぶ」という考え方をすると、同じものを含む順列の総数を組合せの総数で求めることができます。
置き場所を選ぶだけで並べないので組合せ
- nカ所からp個を置く場所の選び方は、nCp通り
- nCp通りのそれぞれについて、n-pカ所から q個を置く場所の選び方は、n-pCq通りずつ
- n-pCq通りのそれぞれについて、n-p-qカ所からr個を置く場所の選び方は、n-p-qCr通りずつ
- 以下、同様
このことから、同じものを含む順列の総数は、組合せの総数を用いて以下のように表されます。
同じものを含む順列と組合せの関係
$n$ 個の中に同じものが $p$ 個、$q$ 個、$r$ 個、……ずつあるとき、その並べ方の総数は、$p$ 個(または $q$ 個、$r$ 個)のものを置く場所を選ぶと考えると
\begin{align*} \quad {}_n \mathrm{ C }_p \times {}_{n-p} \mathrm{ C }_q \times {}_{n-p-q} \mathrm{ C }_r \times \cdots \text{(通り)} \end{align*}ただし
\begin{align*} \quad p + q + r + \cdots = n \end{align*}p個(またはq個、r個)は同じものなので、並べ方を考える必要はありません。
ですから、同じものを含む順列では、同じものをどのように並べるのかではなく、どのように置くのかという発想の方が適切です。
上述のように、順列のように見えても、捉え方によっては組合せで解決できることもあります。何に注目するかをしっかりと考えましょう。これまでをまとめると以下のようになります。
同じものを含む順列を扱った典型的なテーマ
同じものを含む順列を扱った典型的なテーマがいくつかあります。ここでは2つ紹介します。
同じものを含む順列を扱った典型的なテーマ
- 整数の個数
- 最短距離の経路
同じものを含む順列と言えば、この2つのテーマが入試でもよく出題されます。記述形式でも出題されるので慣れておきましょう。
整数の個数
最初のテーマは「整数の個数」です。整数の個数を求める問題では、数字を並べ替えて整数をつくります。
このような問題では、順列の総数を考えることが多いです。
例題1
$1 \ , \ 2 \ , \ 3 \ , \ 4$ の $4$ つの数字を使ってできる $4$ 桁の整数の個数
例題1では、4つの数字に同じものが含まれていません。ですから、例題1は、順列を扱った基本的な問題です。
異なる4つの数字を使って4桁の整数をつくるので、異なる4個のものを並べた順列の総数を求めれば良いことが分かります。
例題1の解答例
$1 \ , \ 2 \ , \ 3 \ , \ 4$ の $4$ つの数字を並べる順列の総数を求めればよいので
\begin{align*} \quad {}_4 \mathrm{ P }_4 &= 4! \\[ 7pt ] &= 4 \cdot 3 \cdot 2 \cdot 1 \\[ 7pt ] &= 24 \text{(個)} \end{align*}計算結果から、異なる4つの数字を使ってできる4桁の整数は全部で24個です。
次の例題2はどうでしょう。
例題2
$1 \ , \ 2 \ , \ 2 \ , \ 4$ の $4$ つの数字を使ってできる $4$ 桁の整数の個数
例題2では、同じ数字が含まれています。ですから、例題2は、同じものを含む順列を扱った問題です。
例題1の4つの数字のうち、3が2に変わったと考えます。例題1で求めた4!個(24個)の整数の中から、重複する個数を除きます。
たとえば、以下のような整数が重複するようになります。
重複ぶんの一例
$1234 \ , \ 1324$ が、例題 $2$ ではともに $1224$ になる。
$3214 \ , \ 2314$ が、例題 $2$ ではともに $2214$ になる。
例題1では、2と3の並べ方が変わると異なる整数になりました。しかし、例題2では同じ整数になります。
2と3の並べ方は2!通りあるので、4つの数字の並べ方4!通りのそれぞれについて、2!通りずつ重複していることが分かります。
例題2の解答例
$1 \ , \ 2 \ , \ 2 \ , \ 4$ の $4$ つの数字を並べる順列の総数 $4!$ のそれぞれについて、$2$ つの $2$ の並べ方 $2!$ 通りずつが重複するので
\begin{align*} \quad \frac{4!}{2!} &= \frac{4 \cdot 3 \cdot 2!}{2!} \\[ 7pt ] &= 12 \text{(個)} \end{align*}計算結果から、1,2,2,4の4つの数字を使ってできる4桁の整数の個数は全部で12個です。
例題1,2のポイントと解答例をまとめると以下のようになります。
例題2では、組合せを利用して整数の個数を求めることができます。「1,2,2,4の数字を4カ所のどこに置くか」を考える問題と捉えることができます。
例題2を組合せで解く
- 4カ所から1個の1を置く場所の選び方は、4C1通り
- 4C1通りのそれぞれについて、3カ所から1個の4を置く場所の選び方は、3C1通りずつ
- 3C1通りのそれぞれについて、2カ所から2個の2を置く場所の選び方は、2C2通りずつ
このときの組合せの総数を計算すると、同じ結果になります。
例題2の別解例
$1 \ , \ 2 \ , \ 2 \ , \ 4$ の $4$ つの数字を並べる順列の総数は、$4$ つの数字の置き方を選ぶ組合せの総数に等しいので
\begin{align*} \quad &{}_4 \mathrm{ C }_1 \times {}_3 \mathrm{ C }_1 \times {}_2 \mathrm{ C }_2 \\[ 7pt ] = \ &4 \cdot 3 \cdot 1 \\[ 7pt ] = \ &12 \text{(個)} \end{align*}順列の総数で求める場合、どうしても重複する並びを含んでしまいます。ですから、最初から重複を除外できる組合せの方が気分的には楽な気がします。
最短距離の経路
次のテーマは「最短距離の経路」です。
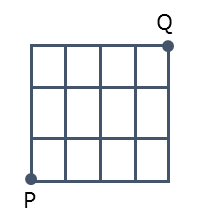
方眼のように縦線と横線でいくつかの区画に分けられています。この縦線や横線を通ってPからQに移動します。
PからQに移動するとき、下方向や左方向に移動すると最短で移動できません。ですから、上方向と右方向の移動だけを考えれば良いことが分かります。
最短距離の経路になるとき、どの経路であっても上方向の移動が3回、右方向の移動が4回の計7回の移動が行われます。
このことから、最短距離の経路は、上方向と右方向の2種類の同じものを含む順列の総数を考えれば良いことが分かります。
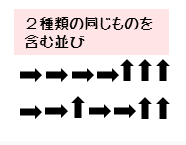
最短距離の経路を考えるとき、上方向または右方向の矢印を並べ替えて経路をつくると分かりやすくなります。
7個の矢印のうち、3個が上方向の矢印で、4個が右方向の矢印です。これらを並べ替えて最短距離の経路を作ります。
このときの順列の総数は以下のようになります。
例題3の解答例
最短距離の経路となるのは上方向の道 $3$ 本と右方向の道 $4$ 本の合計 $7$ 本の道を通るときである。これらを並べたときの順列の総数は
\begin{align*} \quad \frac{7!}{3! \cdot 4!} &= \frac{7 \cdot 6 \cdot 5 \cdot 4!}{3 \cdot 2 \cdot 1 \cdot 4!} \\[ 7pt ] &= 35 \text{(通り)} \end{align*}7個の矢印の並べ方7!通りには、上方向の矢印の並べ方3!通りずつと、右方向の矢印の並べ方4!通りずつとが重複しています。この重複ぶんを除くために除算しています。
また、最短距離の経路が7個の矢印の組合せでできることが分かるので、組合せを利用することもできます。
7カ所のうち、上方向の矢印3個を置く場所の選び方と、右方向の矢印4個を置く場所の選び方を考えます。
このときの経路の求め方は以下のようになります。
例題3の別解例
最短距離の経路となるのは上方向の道 $3$ 本と右方向の道 $4$ 本の合計 $7$ 本の道を通るときである。
経路の総数は、$7$ 本の道のうち、$3$ 本を上方向の道に選び、残り $4$ 本を右方向の道に選ぶときの組合せの総数に等しい。
\begin{align*} \quad {}_7 \mathrm{ C }_3 \times {}_4 \mathrm{ C }_4 &= \frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1} \times 1 \\[ 7pt ] &= 35 \text{(通り)} \end{align*}同じものを含む順列では、順列の総数を利用すると、必ず重複ぶんを除かなければなりません。しかし、組合せなら重複ぶんを除く処理をせずに済みます。
どちらで解くかは好みによりますが、どちらの考え方も理解しておきましょう。
例題3のポイントと解答例をまとめると以下のようになります。
次は、同じものを含む順列を扱った問題を実際に解いてみましょう。