場合の数｜同じものを含む順列について

08/23/2022数学Ａ

同じものを含む順列を扱った問題を解いてみよう

次の問題を考えてみましょう。

問１の解答・解説

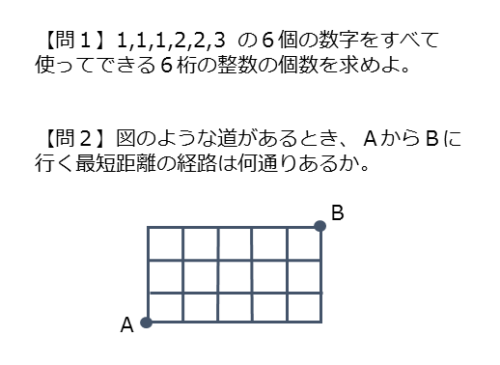
問１

$1 \ , \ 1 \ , \ 1 \ , \ 2 \ , \ 2 \ , \ 3$ の $6$ 個の数字をすべて使ってできる $6$ 桁の整数の個数を求めよ。

６個の数字には同じ種類の数字が含まれています。１が３個、２が２個です。単に順列の総数を数えただけでは、重複ぶんが含まれてしまいます。

３個の１の並べ方３！通りと、２個の２の並べ方２！通りが重複するので、１通りになるように除算します。

問１の解答例

$1$ が $3$ 個、 $2$ が $2$ 個、 $3$ が $1$ 個の合計 $6$ 個を並べる順列の総数は

$\begin{align*} \quad \frac{6!}{3! \cdot 2!} &= \frac{6 \cdot 5 \cdot 4 \cdot 3!}{3! \cdot 2 \cdot 1} \\[ 7pt ] &= 60 \text{（個）} \end{align*}$

問１のポイントと解答例をまとめると以下のようになります。

３の１個についても１！通りで割っても構いませんが、１！＝１であるので計算結果に影響しません。一般にはよく省略されます。

また、計算過程を見ると分かるように、階乗を使った計算では、すべてを乗算に書き直す必要はありません。少しの工夫で計算がラクになるので、ぜひ活用して下さい。

順列ではなく、組合せで解くこともできます。

問１の別解例

$1 \ , \ 1 \ , \ 1 \ , \ 2 \ , \ 2 \ , \ 3$ の $6$ つの数字を並べる順列の総数は、 $6$ つの数字の置き方を選ぶ組合せの総数に等しいので

$\begin{align*} \quad &{}_6 \mathrm{ C }_1 \times {}_5 \mathrm{ C }_2 \times {}_3 \mathrm{ C }_3 \\[ 7pt ] = \ &6 \cdot \frac{5 \cdot 4}{2!} \cdot 1 \\[ 7pt ] = \ &60 \text{（個）} \end{align*}$

組合せを利用する場合、６個の数字を置く場所を選ぶと考えます。ただし、個数の少ない数字から置く場所を選ぶのがコツです。

たとえば、一番個数の少ない数字３、次に数字２、最後に数字１の順に置く場所を選んでいくと、計算が楽になります。

組合せを利用したときのポイントと解答例をまとめると以下のようになります。

場所を選ぶという発想が出てくると組合せを利用できるので、こちらの解き方もしっかりとマスターしておきましょう。

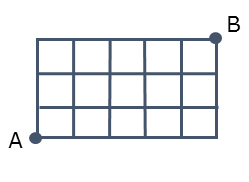
問２の解答・解説

問２

図のような道があるとき、 $A$ から $B$ に行く最短距離の経路は何通りあるか。

最短でＡからＢに行くとき、上方向の移動が３回、右方向の移動が５回の計８回の移動が行われます。

これらを矢印で考えると、上方向の矢印が３個、右方向の矢印が５個の計８個の矢印になります。

この矢印の並べ方の総数が最短距離の経路の総数になります。

問２のポイントと解答例をまとめると以下のようになります。

問２の解答例

$A$ から $B$ に行く最短距離の経路は、縦 $3$ 本、横 $5$ 本の合計 $8$ 本の道を通るときである。

経路の総数は、縦 $3$ 本、横 $5$ 本の合計 $8$ 本の道の順列の総数を求めればよいので

$\begin{align*} \quad \frac{8!}{3! \cdot 5!} &= \frac{8 \cdot 7 \cdot 6 \cdot 5!}{3 \cdot 2 \cdot 1 \cdot 5!} \\[ 7pt ] &= 56 \text{（通り）} \end{align*}$

また、最短距離の経路が８個の矢印の組合せでできることが分かるので、組合せを利用することもできます。

問２の別解例

最短距離の経路となるのは上方向の道 $3$ 本と右方向の道 $5$ 本の合計 $8$ 本の道を通るときである。

経路の総数は、 $8$ 本の道のうち、 $3$ 本を上方向の道に選び、残り $5$ 本を右方向の道に選ぶときの組合せの総数に等しい。

$\begin{align*} \quad {}_8 \mathrm{ C }_3 \times {}_5 \mathrm{ C }_5 &= \frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} \times 1 \\[ 7pt ] &= 56 \text{（通り）} \end{align*}$

組合せを利用したときのポイントと解答例をまとめると以下のようになります。

組合せを利用する場合、個数の少ない上方向の矢印から置く場所を選びましょう。計算が楽になるので、ミスを減らせます。

よく出てくる順列や組合せの計算結果を覚えておこう

順列にしろ組合せにしろ、計算に何度も出てくるものは覚えておくと計算過程を減らせます。

次に挙げるのは一例です。演習でよく見かける計算結果があれば、覚えておきましょう。

覚えておきたい順列や組合せの例

順列

$\begin{align*} &\quad 1! = 1 \\[ 7pt ] &\quad 2! = 2 \cdot 1 = 2 \\[ 7pt ] &\quad 3! = 3 \cdot 2! = 6 \\[ 7pt ] &\quad 4! = 4 \cdot 3! = 24 \\[ 7pt ] &\quad 5! = 5 \cdot 4! = 120 \end{align*}$

組合せ

$\begin{align*} &\quad {}_n \mathrm{ C }_1 = {}_n \mathrm{ C }_{n-1} = n \\[ 7pt ] &\quad {}_n \mathrm{ C }_n = 1 \\[ 7pt ] &\quad {}_3 \mathrm{ C }_2 = {}_3 \mathrm{ C }_1 = 3 \\[ 7pt ] &\quad {}_4 \mathrm{ C }_3 = {}_4 \mathrm{ C }_1 = 4 \\[ 7pt ] &\quad {}_4 \mathrm{ C }_2 = \frac{4 \cdot 3}{2!} = 6 \\[ 7pt ] &\quad {}_5 \mathrm{ C }_3 = {}_5 \mathrm{ C }_2 = \frac{5 \cdot 4}{2!} = 10 \\[ 7pt ] &\quad {}_6 \mathrm{ C }_4 = {}_6 \mathrm{ C }_2 = \frac{6 \cdot 5}{2!} = 15 \\[ 7pt ] &\quad {}_6 \mathrm{ C }_3 = \frac{6 \cdot 5 \cdot 4}{3!} = 20 \end{align*}$

特に、階乗の計算結果を覚えておくと、いちいち掛け算の式を書く必要がなくなります。また、階乗の計算結果を覚えると、階乗の表記のままでも計算できるようになります。