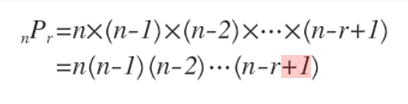場合の数|順列について

今回は頻出の「順列」を学習しましょう。この後に学習する「確率」でも必要な知識になります。順列の定義やその考え方をしっかりマスターしましょう。
記事の画像が見辛いときはクリックすると拡大できます。
順列の定義やその考え方を知ろう
新しい用語とその定義が出てきます。しっかり覚えましょう。
順列に関する基本事項
- 順列
- 階乗
- 順列の総数
順列とは、いくつかの人や物を順番を付けて1列に並べること、または並べたものです。
人や物の単なる組み合わせではなく、並びの順番が大切になってきます。ですから、同じ組合せであっても、並ぶ順番が異なれば別物と捉えます。
次に、階乗です。階乗とは、ある数から1までの整数の積のことです。
一般に、nから1までの整数の積をnの階乗と言い、n!と表します。なお、0の階乗の値は、0!=1と定義されています。
階乗が便利なのは、積を記号化できるところです。たとえば、3×2×1は3の階乗のことなので、3!と表すことができます。
場合の数や確率では、連続する整数の積を頻繁に扱うので、記述を簡略化できる階乗を使いこなせると非常に便利です。
階乗は連続する整数の積を表す
\begin{align*} &\quad 0! = 1 \\[ 7pt ] &\quad n! = n \times \left(n-1 \right) \times \left(n-2 \right) \times \cdots \times 1 \end{align*}さいごに、順列の総数です。順列の総数とは、いくつかの人や物を順番を付けて1列に並べたときの場合の数のことです。
一般に、異なるn個のものからr個を取り出して並べたときの順列の総数を、記号Pを用いてnPrと表します。なお、記号Pは、順列を意味するpermutationの頭文字です。
順列の総数の求め方
A,B,Cの3人を左から順に並べるときの順列の総数を考えてみましょう。順列の総数も場合の数なので、樹形図を書くことで求めることができます。
左端に並ぶ人から順に決めていくと、漏れや重複なしに数え上げることができます。
A,B,Cの3人を左から順に並べるときの順列の総数
- 【左端】A,B,Cの3人がそれぞれ並ぶので3通り
- 【真ん中】左端の3通りのそれぞれについて、残った2人のどちらかが並ぶので2通りずつ
- 【右端】真ん中の2通りのそれぞれについて、最後の1人が並ぶので1通りずつ
樹形図では同じ枝数の樹が3つできます。樹形図において同じ枝数の樹が複数できた場合、積の法則を利用して順列の総数を求めることができます。
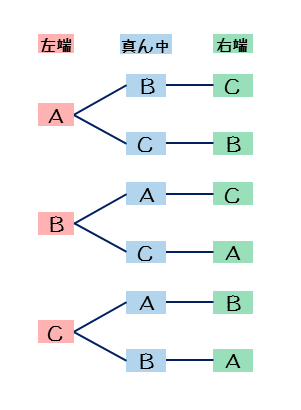
積の法則を利用すると、順列の総数は3×2×1=6(通り)です。順列の総数は連続する整数の積で表されるので、3!(通り)とすることもできます。
階乗の使い方
A,B,Cの3人を左から順に並べるときの順列の総数は、3×2×1=6(通り)でした。このように3人全員であれば、3から1までの整数の積で順列の総数が表されます。
一般に、異なるn個のものすべてを並べるとき、その順列の総数は、nから1までの整数の積で表されます。先ほどの具体例で言えば、「3人を並べるときの順列の総数は3!=3×2×1=6(通り)」のように記述して求めます。
異なるn個を並べるときの順列の総数
\begin{align*} {}_n \mathrm{ P }_n &= n \times (n-1) \times (n-2) \times \cdots \times 1 \\[ 7pt ] &= n! \end{align*}このように、すべての人や物を並べるときの順列の総数は、階乗で表せます。
慣れないうちは整数の積で立式しても構いませんが、たとえば「順列の総数は3!通りあり、~」というふうに文章中にも使えるので、できるだけ早く扱いに慣れておきましょう。
一部の人や物を並べるときの順列の総数
先ほどはすべての人や物を順番に並べたときを考えましたが、次は一部の人や物を並べるときを考えてみましょう。
たとえば、A,B,C,Dの4人のうち、3人を左から順に並べるときの順列の総数を考えます。樹形図は図のようになります。ただし、C,Dが左端のときは省略しています。
A,B,C,Dの4人から3人を左から順に並べるときの順列の総数
- 【左端】A,B,C,Dの4人がそれぞれ並ぶので4通り
- 【真ん中】左端の4通りのそれぞれについて、残った3人のどちらかが並ぶので3通りずつ
- 【右端】真ん中の3通りのそれぞれについて、最後の2人が並ぶので2通りずつ
樹形図では同じ枝数の樹が4つできるので、積の法則を利用できます。
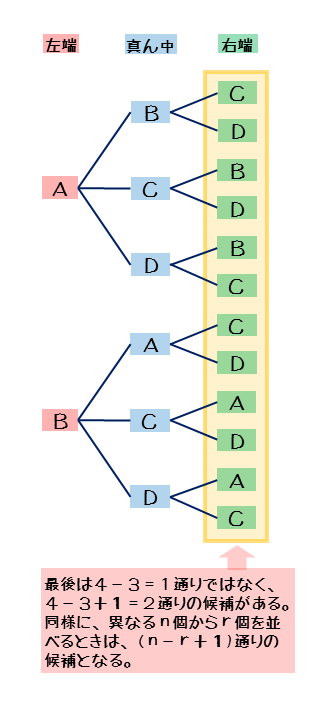
積の法則を利用すると、順列の総数は4×3×2=24(通り)です。
具体例のように4人のうち3人を並べる場合、4から2までの整数の積で表されます。1までではないので注意しましょう。
順列の総数Pの使い方
具体例で分かったことをまとめてみましょう。
3人すべてを並べるときの順列の総数から分かること
- 順列の総数は、連続する整数の積で表される。
- 特に、すべてを並べるとき、ある数から1までの整数の積となり、階乗で表せる。
一部を並べるとき、整数の積は1までの積ではありませんでした。他の場合も同じでしょうか。
全体から一部を並べるときの順列の総数
- 5人のうち4人を並べるとき … 5から2までの積
- 5人のうち3人を並べるとき … 5から3までの積
- 5人のうち2人を並べるとき … 5から4までの積
もう少し例が多ければ規則性に気付くのですが、全体の数から(全体の数)-(並べる数)+1までの積になっています。
一般に、n個の中からr個取って並べるとき、その順列の総数はnからn-r+1までの整数の積で表されます。
以上のことから、すべてまたは一部を並べるときの順列の総数は、記号Pを使って以下のように表せます。
順列の総数
異なる $n$ 個から $r$ 個を並べるときの順列の総数
\begin{align*} \quad {}_n \mathrm{ P }_r = n \cdot \left(n-1 \right) \cdot \left(n-2 \right) \cdot \cdots \cdot \left(n-r+1 \right) \end{align*}異なる $n$ 個を並べるときの順列の総数( $r=n$ のとき)
\begin{align*} \quad {}_n \mathrm{ P }_n &= n \cdot \left(n-1 \right) \cdot \left(n-2 \right) \cdot \cdots \cdot 1 \\[ 5pt ] &= n! \end{align*}すべてを並べるときはr=nのときですが、nPnよりも階乗n!で表すことが多いです。
また、nPrの式で間違いの多いのは、右辺の一番最後の数なので、気を付けましょう。
さらに、nPrの式において、右辺を変形すると以下のような式が得られます。
順列の総数
異なる $n$ 個から $r$ 個を並べるときの順列の総数
\begin{align*} {}_n \mathrm{ P }_r &= n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot (n-r+1) \\[ 10pt ] &= \frac{n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot (n-r+1) \cdot (n-r) \cdot \cdots \cdot 1}{(n-r) \cdot \cdots \cdot 1} \\[ 10pt ] &= \frac{n!}{(n-r)!} \end{align*}下図を見ると、どのように変形したのかが分かると思います。この式であれば階乗だけで表すことができるのが利点です。
順列の総数nPrは2通りの式で表されますが、基本的には整数の積の式を使って順列の総数を求めます。階乗で表した方は、主に証明問題などで使われます。
順列の総数についてまとめると以下のようになります。
順列の総数を求めるときに注意したいこと
階乗やnPrの式について注意したいことがあります。階乗やnPrの式は、あくまでも記述をラクにするためもので、公式ありきではないということです。
場合の数を求めるために、とにかく階乗やnPrを使いたがる人がいます。そのような考え方だと、今後の場合の数や確率で躓くことになります。
そうならないためには、樹形図を書いたり、数え上げの方法を考えたりする発想が先になければなりません。それらを踏まえた結果、順列に当てはまるのであれば、階乗やnPrの式を使えば良いのです。
それに、これまで学習した内容を理解できていれば、場合の数は和の法則や積の法則がベースになっていることが分かるはずです。また、場合の数を求めるとき、その計算のほとんどは簡単な四則計算です。それほど身構える必要はありません。
順列であれば積の法則が成り立つので、掛け算で立式すればそれで足ります。ただ、整数の積を毎回記述するのは煩雑になりがちです。ですから、より平易な記述にするために、階乗やnPrが定義されています。
階乗やnPrは整数の積を記号化するためのもので、必ず使うというわけではありません。
場合の数を求めるときの発想の仕方の例
- 樹形図を書いて、数え上げの方法を調べる
- その結果、順列の考え方で数え上げられそうだと分かる
- nPrで記述を簡略化する
公式や定理を使える条件が揃っていなければ、公式を使っても見当はずれな解答になります。学習の際には、問題に対する考え方や方針について思いを巡らす習慣を付けましょう。
次は実際に問題を解いてみましょう。