数学２
今回は繁分数式の計算について学習しましょう。高校では、数学だけでなく物理や化学などでも繁分数式を扱う機会が多くなります。公式に代入する値が分数のときもあるからです。
繁分数式は、複雑な見た目をしているので、その扱いが難しそうな印象を受けます。しかし、決まった対処法があるので、それに従って扱えば問題ありません。
繁分数式
繁分数式とは、分数の中にさらに分数があるような式です。分母や分子に分数が含まれています。例えば、以下のような式が繁分数式です。
繁分数式の一例
\begin{align*}
&(1) \quad \cfrac{1-\cfrac{1}{x}}{x-\cfrac{1}{x}} \\[ 10pt ]
&(2) \quad \cfrac{1}{1-\cfrac{1}{1-\cfrac{1}{1+a}}}
\end{align*}
どちらの分数式にも分母や分子に分数があります。さすがにこのままだと扱いづらいので、使いやすい形に変形する必要があります。繁分数式の問題では、計算というよりも、与式の変形をする感覚を持っていれば良いでしょう。
繁分数式の計算
繁分数式を計算するには２通りの方法があり、どちらかの方法を選んで計算します。
繁分数式の計算方法は２通り
\begin{align*}
&\text{方法①} \\[ 5pt ]
&\quad \frac{A}{B} = A \div B \\[ 7pt ]
&\text{を利用する。} \\[ 10pt ]
&\text{方法②} \\[ 5pt ]
&\quad \frac{A}{B} = \frac{A \times C}{B \times C} \\[ 7pt ]
&\text{を利用する。}
\end{align*}
どちらの方法を選んでも計算できますが、計算のやりやすさが異なります。与式によって使い分けられるようになりましょう。
繁分数式の計算方法①
計算方法①では、分数式を割り算に戻してしまいます。
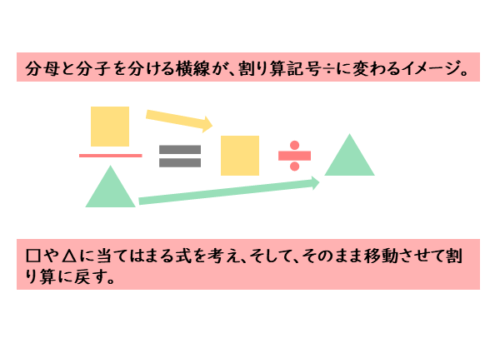繁分数式の計算方法① このことはすでに知っていて簡単だと思うかもしれません。しかし、複雑な繁分数式になると、間違える人が多くなります。どのカタマリが分母や分子なのかを見分けることが難しくなるからです。
例(1)の繁分数式の場合
先ほど挙げた繁分数式の例で考えてみましょう。例(1)の繁分数式を割り算に戻します。
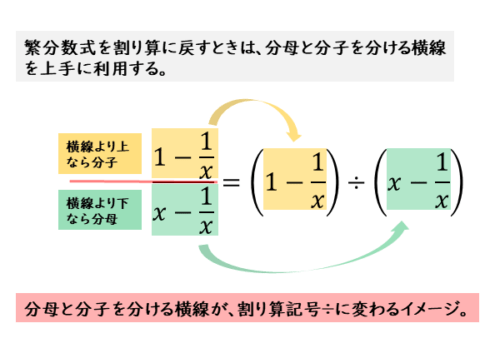繁分数式を割り算に戻す 例(1)の繁分数式は単純な部類に入るので、割り算に戻すことはそれほど難しくないでしょう。
割り算に戻すときのコツは、分母と分子を分ける横線を意識することです。横線よりも下のカタマリが分母で、横線よりも上のカタマリが分子です。
割り算に戻した後の計算例は以下のようになります。
例(1)の計算例
\begin{align*}
\cfrac{1-\cfrac{1}{x}}{x-\cfrac{1}{x}} &= \left( 1-\frac{1}{x} \right) \div \left( x-\frac{1}{x} \right) \quad \text{（通分して１つの分数式にする）} \\[ 12pt ]
&= \frac{x-1}{x} \div \frac{x^{\scriptsize{2}}-1}{x} \quad \text{（掛け算に置き換える）} \\[ 10pt ]
&= \frac{x-1}{x} \times \frac{x}{x^{\scriptsize{2}}-1} \quad \text{（約分できるように因数分解する）} \\[ 10pt ]
&= \frac{x-1}{x} \times \frac{x}{\left(x-1 \right)\left(x+1 \right)} \quad \text{（約分して整理する）} \\[ 10pt ]
&= \frac{1}{x+1}
\end{align*}
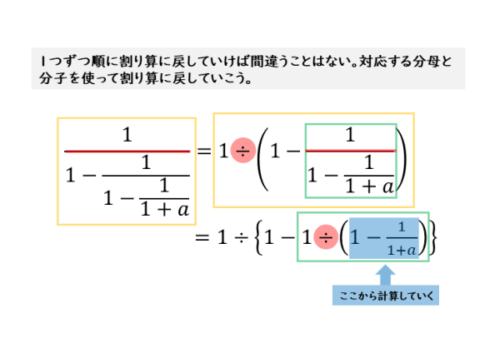
例(2)の繁分数式の場合
例(2)の繁分数式は、例(1)よりも複雑です。分母と分子がどの分数のものかを見分けましょう。コツは、先ほどと同じように分母と分子を分ける横線を意識することです。
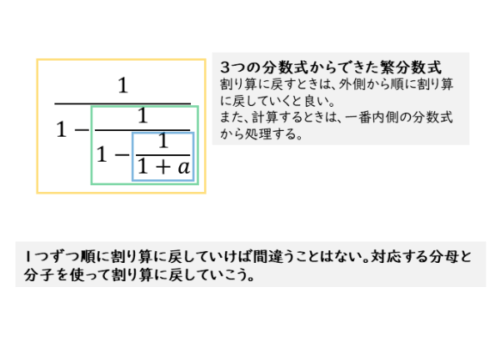３つの分数式からできた繁分数式 一番外側の繁分数式（黄枠）の分母が、分数を含む多項式になっています。そして、その多項式の２番めの項が繁分数式（緑枠）になっています。
さらに、その繁分数式の分母が分数（青枠）を含む多項式になっています。つまり、分母に分数、そしてその分母に分数…というように、入れ子のような繁分数式になっています。
このように複雑な繁分数式を割り算に戻す場合、外側の分数式から順に割り算に戻していくとミスを防ぐことができます。
分母と分子を分ける横線を割り算の記号÷に置き換えるようにします。横線と割り算の記号の個数が一致しているはずです。
このとき、一番内側の分数だけは割り算に戻さず、そのままにしておきましょう。割り算に戻したら計算します。計算のときは内側の分数式から処理していきます。
例(2)の計算例
\begin{align*}
\cfrac{1}{1-\cfrac{1}{1-\cfrac{1}{1+a}}} &= 1 \div \left[ 1- \left\{ 1 \div \left( 1 – \frac{1}{1+a} \right) \right\} \right] \quad \text{（通分して１つの分数式にする）} \\[ 15pt ]
&= 1 \div \left\{ 1- \left( 1 \div \frac{a}{1+a} \right) \right\} \quad \text{（掛け算に置き換える）} \\[ 10pt ]
&= 1 \div \left\{ 1- \left( 1 \times \frac{1+a}{a} \right) \right\} \quad \text{（掛け算する）} \\[ 10pt ]
&= 1 \div \left( 1- \frac{1+a}{a} \right) \quad \text{（通分して１つの分数式にする）} \\[ 10pt ]
&= 1 \div \left( \frac{-1}{a} \right) \quad \text{（掛け算に置き換える）} \\[ 10pt ]
&= 1 \times (-a) \quad \text{（掛け算する）} \\[ 10pt ]
&= -a
\end{align*}
例(2)のような繁分数式では、内側にある分数式から処理していくと計算しやすくなります。
繁分数式の計算方法②
計算方法②は、分母と分子に同じ整式を掛け算するやり方です。イメージとしては分母の有利化に近いです。先ほど挙げた繁分数式を計算してみましょう。
例(1)の繁分数式の場合
例(1)の繁分数式の分母と分子に同じ式を掛けます。分数式が整式となるように、単項式ｘを掛けます。
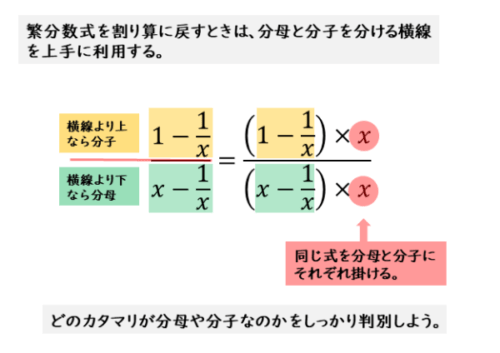繁分数式の計算方法② 式を掛けた後の計算例は以下のようになります。
例(1)の計算例
\begin{align*}
\cfrac{1-\cfrac{1}{x}}{x-\cfrac{1}{x}} &= \cfrac{\left( 1-\cfrac{1}{x} \right) \times x}{\left( x-\cfrac{1}{x} \right) \times x} \quad \text{（分母と分子をそれぞれ展開する）} \\[ 12pt ]
&= \frac{x-1}{x^{\scriptsize{2}}-1} \quad \text{（約分できるように因数分解する）} \\[ 10pt ]
&= \frac{x-1}{(x-1)(x+1)} \quad \text{（約分して整理する）} \\[ 10pt ]
&= \frac{1}{x+1}
\end{align*}
計算方法が異なりますが、もちろん同じ結果になります。
例(2)の繁分数式の場合
例(2)の繁分数式は例(1)よりも複雑ですが、先ほどと同じように、内側の分数式から処理していきます。
分母と分子に同じ式を掛ける
分母に分数、さらに分母に分数…というように、入れ子のようになった繁分数式では、内側の分数から処理しよう。
同じ式を掛けた後の計算例は以下のようになります。
例(2)の計算例
\begin{align*}
\cfrac{1}{1-\cfrac{1}{1-\cfrac{1}{1+a}}} &= \cfrac{1}{1-\cfrac{1 \times (1+a)}{\left(1-\cfrac{1}{1+a} \right) \times (1+a)}} \quad \text{（分母と分子をそれぞれ展開する）} \\[ 15pt ]
&= \cfrac{1}{1-\cfrac{1+a}{(1+a)-1}} \quad \text{（展開した式を整理する）} \\[ 10pt ]
&= \cfrac{1}{1-\cfrac{1+a}{a}} \quad \text{（分母と分子に同じ式を掛ける）} \\[ 10pt ]
&= \cfrac{1 \times a}{\left(1-\cfrac{1+a}{a} \right) \times a} \quad \text{（分母と分子をそれぞれ展開する）} \\[ 10pt ]
&= \frac{a}{a-(1+a)} \quad \text{（展開した式を整理する）} \\[ 10pt ]
&= \frac{a}{-1} \\[ 10pt ]
&= -a
\end{align*}
分母や分子それぞれに式を掛け算しますが、どこまでが１つのカタマリなのかを把握する必要があります。そこで見誤ると計算ミスが起こります。
例(2)のような繁分数式の計算では、一般に計算方法②を用います。ベターなのは、どちらの計算方法も必要に応じて使いこなせることです。１つの繁分数式について、両方のやり方で実際に計算しておきましょう。
次は、繁分数式の計算を実際に解いてみましょう。
