整数の性質|n進法の四則計算について

今回はn進法の四則計算について学習しましょう。10進法での四則計算に慣れ親しんでいるので、2進法や3進法で表される数を使って四則計算する場合、思っている以上に計算ミスをしやすくなります。
どの辺りが間違えやすいのかを把握して、多めに演習をこなしておきましょう。
n進法の四則計算
n進法での四則計算では、10進法のときと同じように筆算することができます。たとえば、加法や減法では、各位の数を縦に揃えて計算します。
10進法と同じ要領で計算できるのですが、計算ミスが多くなるのは「繰り上がり」と「繰り下がり」のときです。
繰り上がりとは、上の桁に数を上げることです。また、繰り下がりとは、下の桁に数を下ろすことです。
「繰り上がり」や「繰り下がり」をどのように行うかは底(nのこと)によって決まりますが、10進法と区別できないと簡単に間違えてしまいます。慣れるまでは丁寧に演習をこなした方が良いでしょう。
2進法での繰り上がりと繰り下がり
繰り上がりと繰り下がりは、記数法の底(nのこと)によって異なります。
たとえば、10進法では、0~9の10個の数字を用いて数を表すので、和が10になると上の位に繰り上げます。足りないときは下の位に10を繰り下げます。他の記数法でも同じ要領で繰り上げたり、繰り下げたりします。
2進法であれば、0と1を用いて数を表す記数法なので、和が2になると上の桁に1だけ繰り上げます。足りないときは下の桁に2を繰り下げます。10ではないので注意しましょう。
2進法での加法や乗法では以下の計算が基本になります。この計算をもとに四則計算を行います。
2進法での加法
\begin{array}{c|cc} + & 0 & 1 \\ \hline 0 & 0 & 1 \\ 1 & 1 & 10 \end{array}2進法での乗法
\begin{array}{c|cc} \times & 0 & 1 \\ \hline 0 & 0 & 0 \\ 1 & 0 & 1 \end{array}2進法での減法と除法
減法では、$10-1 = 1$ に注意。
除法では、乗法と減法を組み合わせて行う。
2進法の加法では、1+1=2とはならず、上の位に1だけ繰り上げて、1+1=10(2)となります。また、2進法の減法では、10-1=9とはならず、下の位に2を繰り下げて、10-1=1(2)となります。
10進法は、0~9の10個の数字を用いて数を表す記数法。
また、2進法は、0と1の2個の数字を用いて数を表す記数法。10や2の意味を分かっていれば、繰り上がりや繰り下がりのミスを防ぐことができる。
例を挙げて確認してみましょう。
例題
次の計算の結果を[ ]内の記数法で表わせ。
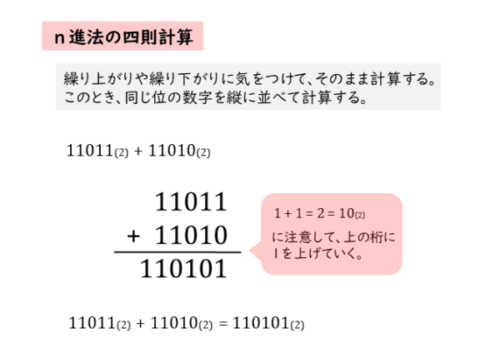
\begin{align*} \quad 11011_{(2)} + 11010_{(2)} \quad \text{[2進法]} \end{align*}数字の右側に(2)という添え字が付いていますが、これは扱う数が2進数であることを示しています。
2進数のままで計算することができるので、位を揃えて縦に計算します。加法のときに注意するのは繰り上がりです。
10進数のときと同じように計算しますが、和が2になると、1+1=10(2)のように、上の位に1だけ繰り上げます。
2進数の加減算であれば、そのまま計算しても問題ないかと思います。どうしても難しいと感じる場合には、次の方法で計算しましょう。
n進法の四則計算でミスをなくす最も確実な方法
一般に、n進法であれば、和がnになると繰り上がり、足りないときはnを繰り下げます。ルール自体は簡単ですが、やはり10進法に慣れているせいかミスしがちです。
n進法の四則計算において、ミスをなくすための最も確実な方法は、n進数を10進数に変換して計算することです。そして、10進数での計算が終わってから、n進数に戻せば良いのです。
先程の例で確認してみましょう。2進数をいったん10進数に変換します。この変換で間違うと、目的を達成できないので注意しましょう。
n進数を10進数に変換する
\begin{align*} &\quad 11011_{(2)} \\[ 7pt ] &= 1 \cdot 2^{4} + 1 \cdot 2^{3} + 0 \cdot 2^{2} + 1 \cdot 2^{1} + 1 \cdot 2^{0} \\[ 7pt ] &= 27 \\[ 10pt ] &\quad 11010_{(2)} \\[ 7pt ] &= 1 \cdot 2^{4} + 1 \cdot 2^{3} + 0 \cdot 2^{2} + 1 \cdot 2^{1} + 0 \cdot 2^{0} \\[ 7pt ] &= 26 \end{align*}10進数に変換できたら、そのまま計算します。計算が終わったら、2で割る割り算を繰り返して2進数に戻します。
10進数をn進数に戻す
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 27 + 26 = 53 \end{align*}より、$10$ 進数 $53$ を $2$ 進数に戻すと
\begin{align*} \quad 53 = 110101_{(2)} \end{align*}記述例は以下のようになります。
記数法の変換についてはすでに学習しているので、簡単に変換できるはずです。ひと手間必要になりますが、計算ミスをなくすことを優先する場合、この方法が最も適切です。
数学では計算ミスは致命的。計算ミスをしない解き方を基本を踏まえて自分なりに構築しよう。
次はn進法の四則計算を扱った問題を実際に解いてみましょう。