物理のヒント集|ヒントその1.距離と変位はどう違うのか

物理の学習で躓きそうな事柄をピックアップしていく企画です。どこまで続くか分かりませんが、ヒント集と言えるくらい記事を書ければ良いなと考えております。参考になれば幸いです。
距離はスカラー量、変位はベクトル量
物理を学習したての頃、戸惑うのが「ベクトル量」と「スカラー量」ではないでしょうか。最初のうちは距離と変位だけでなく、速さと速度の違いにも戸惑うかもしれません。
距離と変位の違いがことばの上で分かっても、実際に計算するときになると使い分けができないことが多々あります。そのような場合、本当の意味で理解できていないということでしょう。
距離と変位の違いについて、具体例を見ながらしっかり理解しましょう。
距離と変位の定義
「距離」とは2点間の長さ、つまり2点間を結んだ線分の長さのことです。距離は長さを表すので、つねに0以上の値(大きさ)をもちます。
一般に、0以上の値をもつことを単に大きさをもつと言ったり、0以上の値をとる数量(長さや面積など)のことを総称して大きさと言ったりすることがある。
「変位」とは空間のどの向きにどれだけ移動したかを表す数量です。言い換えると、変位は基準に対する位置を表すので、向きと距離(大きさ)をもちます。
一般に、大きさだけをもつ数量を「スカラー量」と言うのに対して、向きと大きさをもつ数量を「ベクトル量」と言います。このことから、距離はスカラー量であるのに対して、変位はベクトル量です。
- 距離:大きさだけをもつスカラー量
- 変位:向きと大きさをもつベクトル量
定義の次は、具体例で距離や変位を求めてみましょう。
距離と変位を求めてみよう
図において、右方向を正の向き、左方向を負の向きとします。
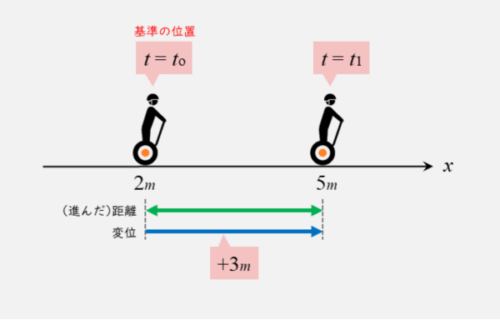
時刻t0に位置x=+2にいた人が、時刻t1に位置x=+5に移動したとします。このとき、人は「時刻t0~t1の間に+3だけ変位」したことになります。また、このときの距離は3です。
実際には以下のように計算して、変位や距離を求めます。
時刻 $t_0 \sim t_1$ の間での変位と距離
変位はベクトル量なので、正負の数を使って計算します。それに対して、距離はスカラー量なので、向きは不要です。ですから、変位の絶対値を使って計算します。
時刻t0~t1の間での変位は、言い換えると時刻t0での位置を初期位置としたときの時刻t1の位置のことです。変位を図示するには、向きと大きさを示す必要があるので矢印を使います。このような基準に対する相対的な位置を表すものを位置ベクトルと言います。
ベクトルは図では矢印。
その後、時刻t2に位置x=-4に移動したとします。向きが正の向きから負の向きへ変わってしまいました。このとき、人は「時刻t0~t2の間に-6だけ変位」したことになります。
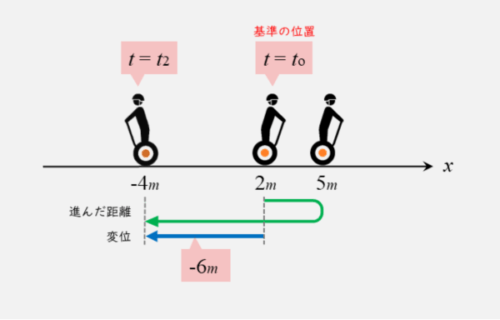
また、このときの距離は6です。変位も距離も、時刻t0と時刻t2の2つの位置で考えることに注意しましょう。
実際には以下のように計算して、変位や距離を求めます。
時刻 $t_0 \sim t_2$ の間での変位と距離
具体例のような一次元(x軸だけ)の運動であれば、変位は、初めの位置からどの向き(±で指定)に、どれだけ移動したのか(2点間の距離)を表すベクトル量になります。
正負の数はベクトル量として扱う。符号は向き、数字は移動量(2点間の距離)。
参考記事:中学数学|正負の数について
次は、距離と道のりの違いについてです。よく間違えるので注意しましょう。
距離と道のりの違い
距離と変位の間違いはもちろんですが、距離と道のりの混同も多く見られます。特に、途中で向きが変わる運動では注意が必要です。
距離は、2点間の長さのことなので「正味で進んだ距離」を表します。
それに対して、道のりは、運動の軌跡の長さのことで、一次元の運動であれば「進んだ距離」を表します。
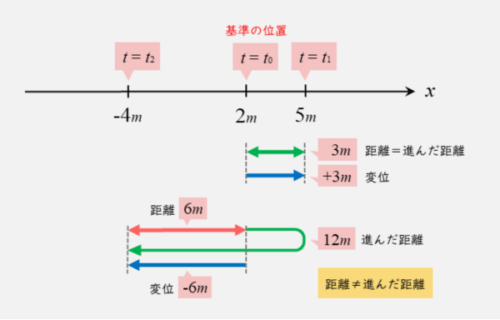
先ほどの具体例で言えば、時刻t0~t1の間での道のりは距離と同じ3になりますが、時刻t0~t2の間での道のりは距離と同じ6になりません。
時刻t0~t2の間での道のりは、時刻t0~t1の間での距離3と、時刻t1~t2の間での距離9との和12になります。
時刻 $t_0 \sim t_2$ の間での道のり
一次元の運動において、途中で向きが変わる場合、正の向きの運動と負の向きの運動とを別々の運動と捉えます。ですから、それぞれの向きごとに距離を求める必要があります。
向きの異なる運動が混在する場合、別々に考えよう。
距離と道のりで迷ったら
「正味で進んだ距離」と明示されず、単に「進んだ距離」や「道のり」などの言葉が使われている場合、一般に、運動の軌跡に沿った道のりを指します。
2点間の長さである距離と、運動の軌跡に沿った道のりのどちらを指しているかは、文脈を注意深く読んで判断しよう。
余談ですが、一般に、距離や道のりは以下のように表されることがあります。微分・積分をまだ学習していない人は飛ばして構いません。
距離と道のりの式
道のりの式では、時刻tにおける速度 $\vec v (t)$ に絶対値がついているので、負の向きの運動も正の向きの運動として扱ったときの距離となります。
具体例のような折り返す運動であれば、折り返さずにそのまま同じ正の向きに運動したときの距離を求めています。
物理・物理基礎のオススメ本
- 宇宙一わかりやすい高校物理(力学・波動)
- 宇宙一わかりやすい高校物理(電磁気・熱・原子)
物理入門者や、物理を苦手にしている人に導入書としておすすめです。教科書が学習の中心であるべきですが、どうしても教科書で理解できない箇所が出てきたら本書で補完すると良いでしょう。イラストが豊富なので独学でも使えます。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
- 秘伝の物理講義[力学・波動]
- 秘伝の物理講義[電磁気・熱・原子]
YouTubeで完全公開されている講義を再現したのが本冊です。また、別冊の「動画テキスト兼ポイント集」で物理の「わからない」を解決できます。公開模試、学校平均点全国No.1を取らせた実力派教師の講義は一読の価値あり。独学にも向き、標準以上も対応可能です。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
物理教室(河合塾series)
所有していますが、これ1冊で基礎から応用まで十分対応できます。理系志望者は一読してほしいのが本書です。
物理の内容が分野ごとに章立てされており、各分野ごとに筋道を通した理解ができます。網羅性が高いのは当然ですが、「物理的な見方や考え方」が自然に身につくように丁寧に解説されています。
また、入試を意識して問題を多く扱っているのも特徴で、問題集代わりにも使えます。基礎を身に着けたい人は参考書として、応用力を養いたい人は問題集として、実力に応じて使いこなせる構成になっています。
問題集の『物理のエッセンス』は有名ですが、同じ河合塾seriesなので相性も良いです。


















