物理のヒント集|ヒントその6.物体に働く力を正しく図示しよう

第6回の物理のヒント集は、物体に働く力の図示についてです。力学では、物体に働く力を正しく図示できれば、ほぼ解けたと言っても過言ではありません。そう言っても良いほど力を正しく図示することは重要です。
力のつり合いを考えるときや運動方程式を立てるとき、力の作用図を利用しながら解くので、必ずマスターしておきましょう。
物体に働く力を正しく図示しよう
さっそく問題です。
例題
ばね定数kのばねに小球A(質量m)がつながれており、軽い糸を介してさらに小球B(質量M)がつながれている。このとき、小球A,Bに働く力の作用図を図示せよ。
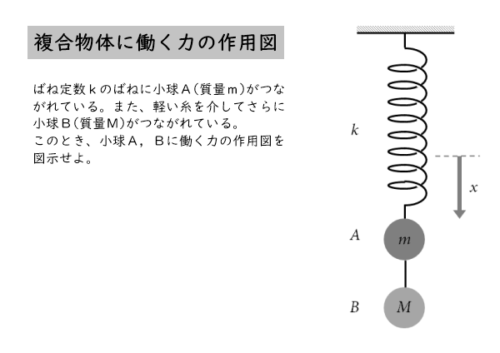
物体に力が働く(作用する)様子を描いた図のことを力の作用図と言います。物体に働く力を矢印(ベクトル)で可視化します。矢印の向きや大きさによって、物体に働く力の様子を把握することができる便利な図です。
物体が1つであれば、力の作用図を描くのに苦労しないでしょう。
しかし、問題では、物体である小球が1つだけでなく2つある複合物体を扱っています。物体が複数になった途端に描けなくなる人がいますが、皆さんはどうでしょうか?
とりあえず、メガネ君の解答を聞いてみましょう。

メガネ先生っ!できましたっ!

メガネ君はいつも元気じゃのぅ。

僕が書いた図は(1),(2)になりますっ!

どれどれ。
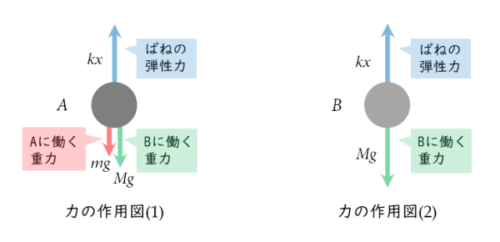

ほほぅ。それでは小球A,Bに働く力を教えてくれんかのぅ。

まず、小球Aでは、上側にばね、下側に小球Bがつながれています。

ですから、上向きに「ばねの弾性力」が働き、下向きに「Aが受ける重力に加えて、Bが受ける重力」も働くと考えました。

なるほどのぅ。次は小球Bじゃの。

小球Bでは、上側にばねがあり、下側に何もありません。

ですから、小球Bには、上向きに「ばねの弾性力」が働き、下向きに「Bが受ける重力」が働くと考えました。

どうですか? 自分ではバッチリだと思うのですがっ!(自画自賛)

自分なりに筋の通った答えを出せるのは偉いぞぃ。

それでは今回こそ大正解ですかっ!(ワクワク)

残念ながら間違いじゃ。

何ですとっ!
物体に働く力には、重力や弾性力などいくつかあります。力の名称を知っていても、それらの図示の仕方を知らなければ問題を解くことはできません。
物体に働く力
物体に働く力には色々な種類があります。力学で主に扱う力は5種類あります。
物体に働く力
- 重力
- 糸の張力
- ばねの弾性力
- 垂直抗力
- 摩擦力
重力
地球上にあるすべての物体は、地球から(その中心に向かって)引かれています。地球から引かれる鉛直下向きの力のことを重力と言います。また、その大きさを重さ(重量)と言います。
重力の大きさは、物体の質量に比例します。また、重力の作用点は、物体の中心(正確には物体の重心)にあります。
一般に、物体に働く重力は、重力加速度と呼ばれる定数を用いて以下のように表されます。
重力
ただし
$W$:重力 $\mathrm{[ N ]}$
$m$:物体の質量 $\mathrm{[ kg ]}$
$g$:重力加速度 $\mathrm{[ m/s^{\scriptsize{2}} ]}$
たとえば、図(1)のように、物体の中心から鉛直下向きに矢印を書き込むと、重力を図示したことになります。
矢印の長さは、他に働く力との大小関係に合わせて調整します。
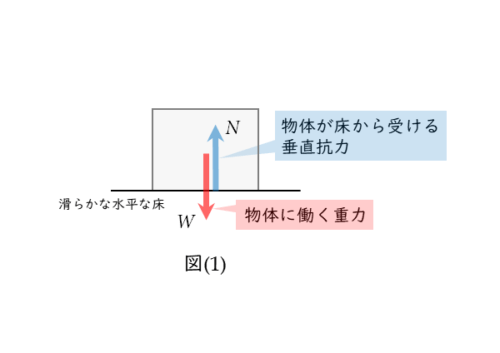
重力は地球上にある物体に必ず働きます。ですから、物体が床の上にあろうが、空中にあろうが、どんな場合でも忘れずに重力を図示しなければなりません。
重力を最優先で図示しよう。物体の中心(重心)から鉛直下向きに図示しよう。
- 作用点:物体の中心(重心)
- 作用線の向き:鉛直下向き
糸の張力
物体に取り付けた糸がピンと張っているとき、糸は糸の方向(糸が物体を引き寄せるよう)に物体を引っ張っています。この力を糸の張力と言います。
基本的に、糸のわずかな伸びは無視され、「伸びない糸」と表現されます。また、糸の質量も無視(m=0)され、「軽い糸」と表現されます。
このような糸であれば、糸の両端での張力は等しいとみなして良いことになっています。つまり、糸の両端以外での張力は無視して良いということです。ですから、張力の作用点は糸の端になります。
図(2)のように、物体を伸びない軽い糸で水平右向きに引っ張っているとします。このとき、物体と接触している左端から水平右向き(=糸の方向)に矢印を書き込むと、張力を図示したことになります。
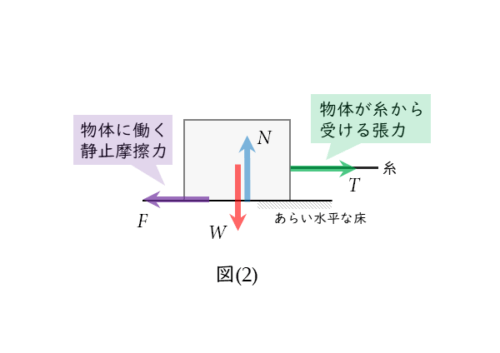
糸の両端(または片端)から、糸の方向に向けて図示しよう。
- 作用点:糸と物体の接触点(糸の端)
- 作用線の向き:糸の方向(糸が引っ張られる方向)
ばねの弾性力
ばねを引き伸ばす(押し縮める)と、ばねは自然長まで縮もう(伸びよう)とします。このとき、ばねに取り付けてある物体に力を及ぼします。この力のことをばねの弾性力と言います。
弾性力の大きさは、ばね定数とばねの伸び(縮み)によって決まります。これをフックの法則と言います。関係式は以下のように表されます。
フックの法則
ただし
$F$:ばねの弾性力の大きさ $\mathrm{[ N ]}$
$k$:ばね定数 $\mathrm{[ N/m ]}$
$x$:ばねの伸びまたは縮み $\mathrm{[ m ]}$
一般に、ばねの質量も糸と同じように無視されます。ですから、軽いばねの場合、ばねの両端での弾性力は等しいとみなします。また、ばねの弾性力の作用点は、ばねの端になります。
張力と区別したいのは、力の働く向きです。張力が必ず糸の方向に働くのに対して、ばねの伸びまたは縮みによって、弾性力の働く向きが変わります。
ばねの端から、ばねに沿う向きに図示しよう。ただし、向きに注意。
- 作用点:ばねと物体の接触点(ばねの端)
- 作用線の向き:ばねに沿う方向(伸びなら縮む方向、縮みなら伸びる方向)
詳細は第5回の記事を参照して下さい。
垂直抗力
水平な床の上に置かれた物体は、重力が鉛直下向きに働いているにもかかわらず、床にめり込むことなく床の上にあり続けます。
これは、物体に対して、重力と同じ大きさの力が鉛直上向きに働いているからです。この力のことを垂直抗力と言います。
垂直抗力は、床が物体を押し戻そうとする力のことで、物体が接触する面に対して垂直に働きます。このとき、垂直抗力の作用点は物体と接触している面上(床の表面)にあります。
たとえば、図(1)のように、水平な床の上に物体が置かれているとき、物体には重力と垂直抗力が働いており、この2力がつり合っています。
物体は水平な床に置かれているので、床の表面から、床面に対して垂直に物体を押し戻す向き、つまり鉛直上向きに矢印を書くと、垂直抗力を図示したことになります。

ここでは、重力と垂直抗力がつり合うので、作用線( 矢印 )の長さは同じにします。
物体との接触面から、物体を押し戻す向きに図示。ただし、向きは接触面に対して垂直。
- 作用点:物体との接触面のどこかにとる
- 作用線の向き:接触面に垂直で、物体を押し戻す向き
摩擦力
あらい水平な床の上にある物体を水平方向に動かすとき、物体はスムーズに動きません。それは、動かそうとする向きとは逆向きに、妨げる力が物体と床の間に働いているからです。
このように物体と床が接触している面が滑るのを妨げるように働く力のことを摩擦力と言います。
摩擦力は物体が運動する向き(または運動しようとする向き)と逆向きに働きます。基本的に、物体は床に沿って運動するので、摩擦力は、床面に沿う向きに働きます。このとき、作用点は、物体と床の間(接触面)にあります。
たとえば、図(2)のように、あらい水平な床の上にある物体を、右側に取り付けた糸で水平右向きに引っ張りましたが、それでも物体が静止したままだったとします。

鉛直方向では、重力と垂直抗力がつり合っています。水平方向では、糸の張力が水平右向きに物体に働くので、物体は水平右向きに運動しようとします。
しかし、摩擦力が張力と同じ大きさで、かつ逆向き(水平左向き)に働いています。このことから、水平方向の力がつり合い、物体が静止したままになっています。
物体と床の間に、糸の張力と逆向きに矢印を書くと、摩擦力を図示したことになります。ここでは、張力と摩擦力はつり合うので、作用線( 矢印 )の長さは同じにします。
ここでは詳しく解説しませんが、物体の状態に応じた摩擦力があります。
摩擦力の分類
- 物体が静止しているときに働く摩擦力=静止摩擦力
- 物体が運動しているときに働く摩擦力=動摩擦力
図(2)では、物体が静止しているので、静止摩擦力です。
物体と床の間(接触面)から、接触面に沿って図示しよう。ただし、運動を妨げる向き。
- 作用点:物体と床の接触面のどこかにとる
- 作用線の向き:物体の運動を妨げる向き
5種類の力のことが分かったところで、次は問題を改めて解き直してみましょう。









