図形と方程式|2つの円の交点を通る円や直線について

今回は、2つの円の交点を通る円や直線について学習しましょう。
2つの円の交点を通る円や直線に関する問題は、一見すると難しくて面倒そうな感じのする問題です。しかし、決まったパターンで解くことができるので、比較的早く習得することができます。
入試でもたびたび出題されますが、確実に解ける問題にしておいて得点源にしましょう。
2つの円の交点を通る円や直線
2つの円の交点を通る円や直線は、以下の式で表されます。
2つの円の交点を通る円や直線 1⃣
異なる $2$ 点 $P \ , \ Q$ で交わる $2$ つの円
\begin{align*} &\quad x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1}=0 \ \cdots \ \text{(※)} \\[ 7pt ] &\quad x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}に対し、$k$ を定数とすると、方程式
\begin{align*} \quad k \left(x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1} \right)+x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}は、$2$ つの円の交点を通る円または直線を表す。
この式は2つの円の交点を通る円や直線を表しますが、どのようにして得られたのかピンとこない人もいるでしょう。
そこで、2つの円の交点の座標を考えます。交点の座標を求めるには、2つの円の方程式を連立して解きます。この連立方程式から上述の式を導出することができます。
2つの円の交点を通る円や直線の導出
異なる $2$ 点 $P \ , \ Q$ で交わる $2$ つの円
\begin{align*} &\quad x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1}=0 \\[ 7pt ] &\quad x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}に対し、$2$ 点 $P \ , \ Q$ の座標は連立方程式
\begin{align*} \left\{ \begin{array}{l} x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1}=0 \ \cdots \ \text{①} \\[ 7pt ] x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \ \cdots \ \text{②} \end{array} \right. \end{align*}の解である。ここで、$k$ を定数とすると、①$\times k+$②より
\begin{align*} \quad k \left(x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1} \right)+x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}つまり、連立方程式のように別々に記述していたものから、1つの式にまとめたものだと解釈できます。1つにまとめてしまいましたが、交点の座標を代入すると等式が成り立つので全く問題ありません。
また、上式では、カッコの中の式は(※)式の左辺ですが、他方の左辺でも問題ありません。たとえば、以下の2つの式で考えてみましょう。
2つの円の交点を通る円や直線の例 1⃣
異なる $2$ 点 $P \ , \ Q$ で交わる $2$ つの円
\begin{align*} &\quad x^{2}+y^{2}+6x-4y+4=0 \\[ 7pt ] &\quad x^{2}+y^{2}-4=0 \end{align*}に対し、$k$ を定数とすると、方程式
\begin{align*} \quad k \left(x^{2}+y^{2}+6x-4y+4 \right)+x^{2}+y^{2}-4=0 \ \cdots \ \text{③} \end{align*}または
\begin{align*} \quad k \left(x^{2}+y^{2}-4 \right)+x^{2}+y^{2}+6x-4y+4=0 \ \cdots \ \text{④} \end{align*}は、$2$ つの円の交点を通る円または直線を表す。
例のように、2つの円の交点を通る円や直線の表し方は2通りあります。③式と④式のどちらを採用するかは、それぞれ展開したときを考えると分かります。
カッコのある項を展開したとき、定数kが5つの項に掛けられる③式よりも、3つの項に掛けられる④式の方が扱いやすいでしょう。
カッコの中の式は、できるだけ項の少ない方にしよう。
上式は2つの円の交点を通る円や直線を表しますが、円の方程式だけを知りたい場合が出てくるでしょう。逆に、直線の方程式を知りたい場合もあるでしょう。そこでポイントになるのが、定数kの値です。
2つの円の交点を通る円や直線 2⃣
異なる $2$ 点 $P \ , \ Q$ で交わる $2$ つの円
\begin{align*} &\quad x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1}=0 \ \cdots \ \text{(※)} \\[ 7pt ] &\quad x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}に対し、$k$ を定数とすると、方程式
\begin{align*} \quad k \left(x^{2}+y^{2}+l_{1}x+m_{1}y+n_{1} \right)+x^{2}+y^{2}+l_{2}x+m_{2}y+n_{2}=0 \end{align*}は、$2$ つの円の交点を通る円または直線を表す。特に
$\quad k \neq -1$ のとき、$2$ つの交点 $P \ , \ Q$ を通る円((※)を除くすべての円)
$\quad k = -1$ のとき、$2$ つの交点 $P \ , \ Q$ を通る直線
kの値が-1以外であれば、(※)式以外の円を表すことができます。ただし、2つの円のうち、(※)式の円を表すことはできません。
また、k=0のときであれば、他方の円を表すことができるので注意しましょう。
2つの円の交点を通る円や直線の例 2⃣
異なる $2$ 点 $P \ , \ Q$ で交わる $2$ つの円
\begin{align*} &\quad x^{2}+y^{2}+6x-4y+4=0 \\[ 7pt ] &\quad x^{2}+y^{2}-4=0 \end{align*}に対し、$k$ を定数とすると、方程式
\begin{align*} \quad k \left(x^{2}+y^{2}-4 \right)+x^{2}+y^{2}+6x-4y+4=0 \end{align*}は、$2$ つの円の交点を通る円または直線を表す。
ここで、$k=0$ を代入すると
\begin{align*} \quad 0 \times \left(x^{2}+y^{2}-4 \right)+x^{2}+y^{2}+6x-4y+4=0 \end{align*}より
\begin{align*} \quad x^{2}+y^{2}+6x-4y+4=0 \end{align*}これはもとの $2$ つの円のうちの $1$ つである。
また、$k=-1$ を代入すると
\begin{align*} \quad -1 \times \left(x^{2}+y^{2}-4 \right)+x^{2}+y^{2}+6x-4y+4=0 \end{align*}より
\begin{align*} \quad 6x-4y+8=0 \end{align*}よって
\begin{align*} \quad 3x-2y+4=0 \end{align*}これは $2$ つの円の交点を通る直線を表す。
k≠-1であるのは、円の方程式がx,yの2次の項をそれぞれもつからです。
また、2つの円の交点を通る直線は1次式なので、これを満たすのはk=-1のときだけです。
k≠-1であれば円の方程式、k=-1であれば直線の方程式を表す。
2つの曲線の交点を通る曲線
2つの円の交点を通る円や直線を表す式を一般化すると、以下のように表されます。
2つの曲線の交点を通る曲線
$2$ つの曲線
\begin{align*} &f \left(x \ , \ y \right)=0 \\[ 7pt ] &g \left(x \ , \ y \right)=0 \end{align*}に対し、$k$ を定数とすると、方程式
\begin{align*} \quad k f \left(x \ , \ y \right)+g \left(x \ , \ y \right)=0 \end{align*}は、$2$ つの曲線の交点を通る曲線を表す。
f(x,y)=0やg(x,y)=0は、x,yを変数にもつ方程式を表します。ここで扱う円や直線の方程式の左辺を想像すると良いでしょう。
次は例題を解きながら、2つの円の交点を通る円や直線を求めてみましょう。
2つの円の交点を通る円や直線を調べてみよう
次の例題を解いてみましょう。
例題
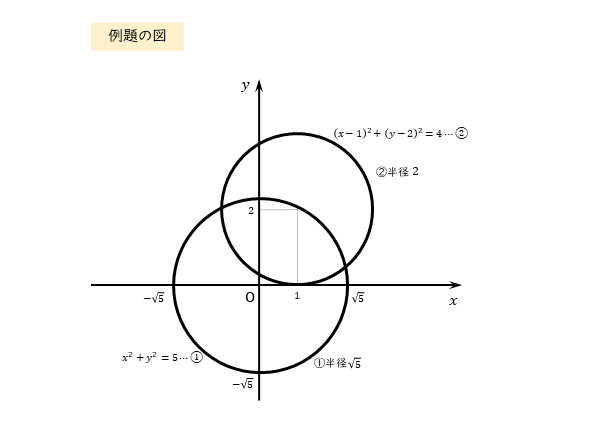
$2$ つの円
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}について
$(1) \quad 2$ つの円は、異なる $2$ 点で交わることを示せ。
$(2) \quad 2$ つの円の交点を通る直線の方程式を求めよ。
$(3) \quad 2$ つの円の交点と点 $(0 \ , \ 3)$ を通る円の中心と半径を求めよ。
例題(1)の解答・解説
例題(1)
$2$ つの円
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}について
$\quad 2$ つの円は、異なる $2$ 点で交わることを示せ。
例題(1)は、2つの円が異なる2点で交わることを示す問題です。一般に、連立方程式を解けば、交点の座標を求めることができます。
「交点の座標を求めよ」とは指示されていませんが、交点の座標を2組求めることができれば何とかなりそうです。
ここで厄介なことがあります。扱う2つの方程式が円の方程式であるということです。この場合、連立方程式を解く方法では上手くいきそうにありません。
そこで思い出したいのが、2つの円の位置関係です。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とすると
$(1) \ 2$ つの円が外接する
\begin{align*} \quad d=r+r’ \end{align*}$(2) \ 2$ つの円が内接するか、一致する場合
\begin{align*} \quad d=\left| r-r’ \right| \end{align*}$(1) \ , \ (2)$ を合わせて、$2$ つの円が共有点をもつ場合
\begin{align*} \quad \left| r-r’ \right| \leqq d \leqq r+r’ \end{align*}例題(1)では異なる2点で交わるときを考えるので、外接するときと内接するときを除きます。つまり、等号のない不等式が成り立てば良いということです。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とすると
$2$ つの円が異なる $2$ つの共有点をもつ場合
\begin{align*} \quad \left| r-r’ \right| \lt d \lt r+r’ \end{align*}が成り立つ。
これを踏まえて例題(1)を解きます。
例題(1)の解答例
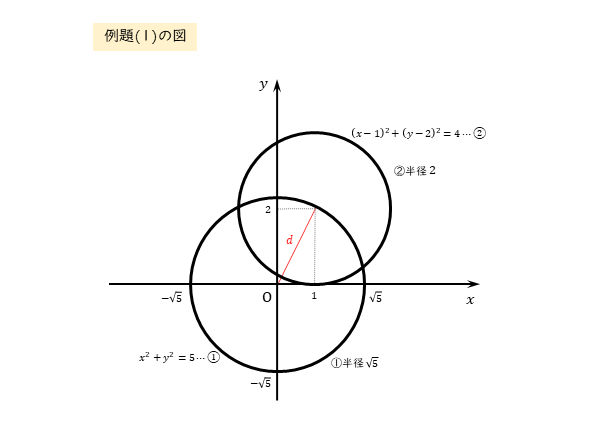
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}円①の半径は $\sqrt{5}$、②の半径は $2$ である。
また、円①の中心は $(0 \ , \ 0)$、円②の中心は $(1 \ , \ 2)$ である。
中心間の距離を $d$ とすると
\begin{align*} \quad d=\sqrt{1^{2} + 2^{2}}=\sqrt{5} \end{align*}であるので
\begin{align*} \quad \left| \sqrt{5}-2 \right| \lt d \lt \sqrt{5}+2 \end{align*}が成り立つ。
よって、$2$ 円①,②は異なる $2$ 点で交わる。
連立方程式を解くよりも容易に証明することができました。性質を上手に利用できるようにしましょう。
例題(2)の解答・解説
例題(2)
$2$ つの円
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}について
$\quad 2$ つの円の交点を通る直線の方程式を求めよ。
定数kを用いて、2つの方程式を1つにまとめます。
例題(2)の解答例 1⃣
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}$k$ を定数とすると、①,②から
\begin{align*} \quad k \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \ \cdots \ \text{③} \end{align*}③は $2$ つの円①,②の交点を通る円、または直線を表す。
2つの円の交点を通る円や直線を表す③式を導出することができました。カッコの中の式は②式でも構いませんが、後々のことを考えると①式の方が良いでしょう。
ここで注意したいのは、①,②式の右辺を0にしてから③式を導出するということです。
例題(2)のよくある間違い
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}$k$ を定数とすると、①,②から
\begin{align*} \quad k \left( \underline{x^{2}+y^{2}} \right)+\underline{\left(x-1 \right)^{2}+\left(y-2 \right)^{2}} = 0 \ \cdots \ \text{③} \end{align*}③に $2$ つの円①,②の交点座標を代入しても等式は成り立たないので不適。
正しくは①,②式の右辺を $0$ にした式を使う。
①より
\begin{align*} \quad x^{2}+y^{2}-5 = \underline{0} \end{align*}②より
\begin{align*} \quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4= \underline{0} \end{align*}$k$ を定数とすると
\begin{align*} \quad k \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \end{align*}例題のように①,②式の右辺が0であることを確認してから1つにまとめましょう。
この単元の解法はワンパターンで簡単なこともあり、このような引っ掛け問題であるのが特徴です。ここで間違えることが非常に多いので注意しましょう。
1つにまとめるのは、円の方程式の右辺を0にしてから。
2つの円の交点を通る直線は、③式においてK=-1のときの方程式です。③式にK=-1を代入して整理します。
例題(2)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] \quad &k \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \ \cdots \ \text{③} \end{align*}③に $k=-1$ を代入すると
\begin{align*} \quad – \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \end{align*}これを整理すると
\begin{align*} &\quad 5-2x+1-4y+4-4 = 0 \\[ 7pt ] &\quad -2x-4y+6 = 0 \\[ 7pt ] &\quad x+2y-3= 0 \end{align*}これは $x \ , \ y$ の $1$ 次式であるので直線を表す。
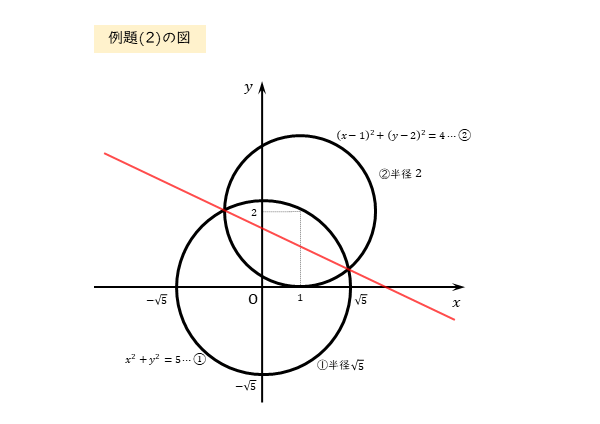
よって、求める直線の方程式は
\begin{align*} \quad x+2y-3= 0 \end{align*}k=-1を代入するのは、x,yの2次の項を消去するためです。ですから、式を整理するとき、x,yの2次の項を記述していません。
予想通りに傾きが負となるような方程式が得られました。作図しておくと検算にも役立ちます。
例題(3)の解答・解説
例題(3)
$2$ つの円
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}について
$\quad 2$ つの円の交点と点 $(0 \ , \ 3)$ を通る円の中心と半径を求めよ。
例題(3)は、2つの円の交点を通る円の方程式を求める問題です。
例題(2)の③式において、k≠-1であれば、2つの円の交点を通る円になります。
しかし、点(0,3)を通る円かどうかは分かりません。
点(0,3)を通る円となるために、kの値を適切に決める必要があります。
例題(2)の③式は、2つの円の交点の座標を代入すると等式が成り立つ方程式です。ですから、あとは点(0,3)を③式に代入しても等式が成り立つことを考えます。
③式に点(0,3)を代入して、kについての方程式を導出します。
例題(3)の解答例 1⃣
\begin{align*} &\quad \vdots \\[ 7pt ] \quad &k \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \ \cdots \ \text{③} \\[ 7pt ] &\quad \vdots \end{align*}③が点 $(0 \ , \ 3)$ を通る円であるためには、③に $x=0 \ , \ y=3$ を代入したときに等式が成り立てばよい。
よって
\begin{align*} \quad k \left(0^{2}+3^{2}-5 \right)+\left(0-1 \right)^{2}+\left(3-2 \right)^{2}-4 = 0 \end{align*}これを整理すると
\begin{align*} \quad 4k+1+1-4 &= 0 \\[ 7pt ] k &= \frac{1}{2} \end{align*}kの値を得ることができました。これが2つの円の交点だけでなく、点(0,3)も通るときのkの値です。
円の中心と半径を求めるために、求めたkの値を③式に代入します。
例題(3)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] \quad &k \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \ \cdots \ \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] \quad &k= \frac{1}{2} \end{align*}これを③に代入して整理すると
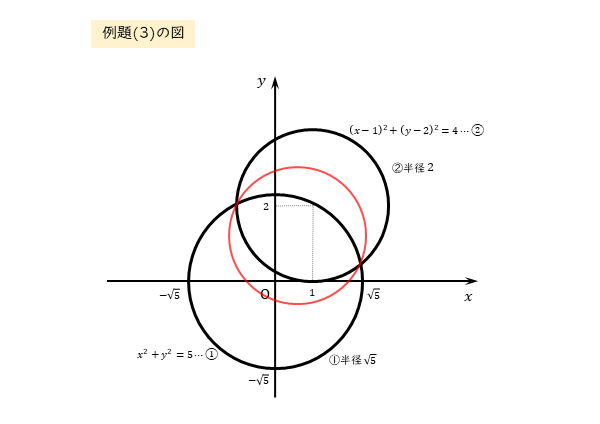
\begin{align*} &\quad \frac{1}{2} \left(x^{2}+y^{2}-5 \right)+\left(x-1 \right)^{2}+\left(y-2 \right)^{2}-4 = 0 \\[ 7pt ] &\quad x^{2}+y^{2}-5+2 \left(x-1 \right)^{2}+2 \left(y-2 \right)^{2}-8 = 0 \\[ 7pt ] &\quad 3x^{2}-4x+3y^{2}-8y-5+2+8-8 = 0 \\[ 7pt ] &\quad 3x^{2}-4x+3y^{2}-8y-3 = 0 \\[ 7pt ] &\quad x^{2}-\frac{4}{3}x+y^{2}-\frac{8}{3}y-1 = 0 \\[ 7pt ] &\quad \left(x-\frac{2}{3} \right)^{2}+\left(y-\frac{4}{3} \right)^{2}-\frac{4}{9}-\frac{16}{9}-1 = 0 \\[ 7pt ] &\quad \left(x-\frac{2}{3} \right)^{2}+\left(y-\frac{4}{3} \right)^{2}-\frac{29}{9} = 0 \\[ 7pt ] &\quad \left(x-\frac{2}{3} \right)^{2}+\left(y-\frac{4}{3} \right)^{2} = \frac{29}{9} \\[ 7pt ] &\quad \left(x-\frac{2}{3} \right)^{2}+\left(y-\frac{4}{3} \right)^{2} = \left(\frac{\sqrt{29}}{3} \right)^{2} \end{align*}よって、求める円の中心は
\begin{align*} \quad \left(\frac{2}{3} \ , \ \frac{4}{3} \right) \end{align*}また、円の半径は
\begin{align*} \quad \frac{\sqrt{29}}{3} \end{align*}kの値が分数だったので、少し丁寧に式変形しています。
ここでは、平方完成をする前に2次の項の係数を1にしています。3でくくるよりも、両辺を3で割った方が計算ミスをしにくいだろうと考えたからです。
そのせいで式変形がやや煩雑になっています。そうは言っても、入試では分数を必ず扱うので、式変形に慣れておきましょう。
2つの円の交点の座標を求めるには
余談になりますが、2つの円の交点の座標を求めることを考えてみましょう。
例題(1)の解説で、2つの円の方程式を連立して解くことは難しい(できないと考えて良い)と述べました。このような場合、2つの円の方程式を連立するのではなく、円と直線の方程式を連立します。
2つの円の交点を通る直線の方程式を求めるには、例題(2)の解法を利用します。
例題(2)の解法を用いて、2つの円の交点を通る直線の方程式を求めたら、これとどちらか一方の円の方程式を連立します。ここでは、円①の方程式と連立した方が良いでしょう。
2つの円の交点を通る直線を求める
\begin{align*} &\quad x^{2}+y^{2}=5 \ \cdots \ \text{①} \\[ 7pt ] &\quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \ \cdots \ \text{②} \end{align*}円①,②の交点を通る直線の方程式は、$(2)$ より
\begin{align*} \quad x+2y-3=0 \end{align*}$x$ について整理すると
\begin{align*} \quad x=-2y+3 \end{align*}これと①より
\begin{align*} \quad \left(-2y+3 \right)^{2}+y^{2}=5 \end{align*}これを整理すると
\begin{align*} &\quad 5y^{2}-12y+9=5 \\[ 7pt ] &\quad 5y^{2}-12y+4=0 \\[ 7pt ] &\quad 5y^{2}-2 \cdot 6y+4=0 \end{align*}解の公式より
\begin{align*} \quad y &=\frac{-\left(-6 \right) \pm \sqrt{\left(-6 \right)^{2}-5 \cdot 4}}{5} \\[ 7pt ] &= \frac{6 \pm \sqrt{16}}{5} \\[ 7pt ] &= \frac{6 \pm 4}{5} \\[ 7pt ] &= \frac{2}{5} \ , \ 2 \end{align*}$y=\frac{2}{5}$ のとき
\begin{align*} \quad x &= -2 \cdot \frac{2}{5}+3 \\[ 7pt ] &= -\frac{4}{5}+3 \\[ 7pt ] &= \frac{11}{5} \end{align*}$y=2$ のとき
\begin{align*} \quad x &= -2 \cdot 2+3 \\[ 7pt ] &= -4+3 \\[ 7pt ] &= -1 \end{align*}よって、$2$ つの円の交点の座標は
\begin{align*} \quad \left(\frac{11}{5} \ , \ \frac{2}{5} \right) \ , \ \left(-1 \ , \ 2 \right) \end{align*}直線の方程式を変形するとき、yについて変形してから①式に代入しても構いません。
ただし、係数が分数になってしまうので良い解法とは言えません。
なお、分数が出てくると何だか不安になりますが、図で確認してみると良いでしょう。
それほどおかしな座標ではないようです。
次は、2つの円の交点を通る円や直線を扱った問題を実際に解いてみましょう。