数学1
今回は、データの相関関係について学習しましょう。
ここでは、主に2つの変量の相関を考えます。相関関係を表す量や図があり、それらから2つの変量の相関の強さや傾向を知ることができます。
この単元でも頻出の公式が出てくるので、しっかり使えるようにしておきましょう。
この単元で学習すること
「データの相関関係」では以下のような事柄を学習します。
これらはデータの相関関係を知るためのものです。1つずつ丁寧に確認していきましょう。
散布図
身長と体重の関係や小テストと定期テストの関係など、2つの変量x,yの間の関係を考えることがあります。2つの変量が以下のように定義されているとします。
変量とデータの各値
\begin{align*}
&\text{$2$ つの変量 $x \ , \ y$ について、} \\[ 5pt ]
&\text{データの大きさがともに $n$ 個であり} \\[ 5pt ]
&\quad x_{\scriptsize{1}} \ , \ x_{\scriptsize{2}} \ , \cdots \cdots , \ x_{\scriptsize{n}} \\[ 7pt ]
&\quad y_{\scriptsize{1}} \ , \ y_{\scriptsize{2}} \ , \cdots \cdots , \ y_{\scriptsize{n}} \\[ 7pt ]
&\text{とする。}
\end{align*}
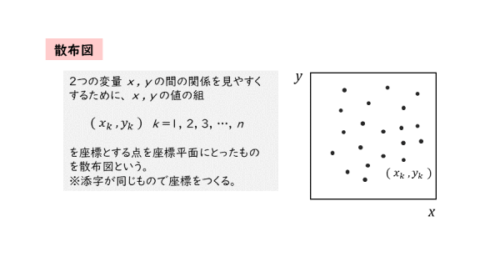
このように定義される2つの変量について、x,yの関係を見やすくするために、座標平面を利用することがあります。このとき、x,yの値の組を座標とする点を座標平面上にとります。
点の座標
\begin{align*}
&\text{$x \ , \ y$ の値の組} \\[ 5pt ]
&\quad ( x_{\scriptsize{k}} \ , \ y_{\scriptsize{k}} ) \quad k = 1 \ , \ 2 \ , \cdots \cdots , \ n \\[ 7pt ]
&\text{を座標とする点を座標平面上にとる。}
\end{align*}
x,yの値の組は添字が同じものです。このような点を座標平面上にとったものを散布図と言います。点が散って分布している図という意味です。
散布図の例は以下のようになります。
 散布図について
散布図について 相関関係
散布図から2つの変量の間にどんな相関関係があるのかを把握することができます。相関の関係は主に3つに分類されるので、散布図も3パターンになります。
散布図と相関の関係は3パターン
- 正の相関関係を表す散布図
- 負の相関関係を表す散布図
- 相関関係がないことを表す散布図
正の相関関係
2つの変量のデータにおいて、一方が増えると他方も増える傾向が認められるとき、2つの変量の間に正の相関関係があると言います。
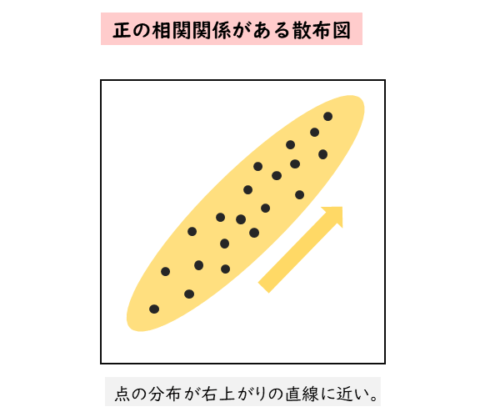
正の相関関係がある散布図は以下のようになります。
 正の相関関係がある散布図
正の相関関係がある散布図 点の分布が右上がりの直線に近いものになります。
負の相関関係
それに対して、一方が増えると他方が減る傾向が認められるとき、2つの変量の間に負の相関関係があると言います。
負の相関関係がある散布図は以下のようになります。
 負の相関関係がある散布図
負の相関関係がある散布図 点の分布が右下がりの直線に近いものになります。
相関関係がない
どちらの傾向も認められなければ、2つの変量の間に相関関係がないと言います。
相関関係がない散布図は以下のようになります。
 相関関係がない散布図
相関関係がない散布図 点の分布が一様で偏りがないものになります。
散布図に見られる傾向と相関関係をまとめると以下のようになります。
散布図に見られる傾向と相関関係
- 正の相関がある:一方が増えると他方も増える傾向がある
- 負の相関がある:一方が増えると他方は減る傾向がある
- 相関がない:どちらの傾向もない
あくまでも散布図を見たとき、点の分布から読み取れる相関関係です。
共分散
xの偏差とyの偏差の積の平均値を共分散と言います。共分散は以下のように表されます。
共分散
\begin{align*}
&\text{共分散を $s_{\scriptsize{xy}}$ とすると、} \\[ 5pt ]
&\quad s_{\scriptsize{xy}} = \frac{1}{n} \left\{ ( x_{\scriptsize{1}} \ – \overline{x} ) ( y_{\scriptsize{1}} \ – \overline{y} ) + ( x_{\scriptsize{2}} \ – \overline{x} ) ( y_{\scriptsize{2}} \ – \overline{y} ) + \cdots \cdots + ( x_{\scriptsize{n}} \ – \overline{x} ) ( y_{\scriptsize{n}} \ – \overline{y} ) \right\} \\[ 10pt ]
&\text{または} \\[ 5pt ]
&\quad s_{\scriptsize{xy}} = \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } ( x_{\scriptsize{k}} \ – \overline{x} ) ( y_{\scriptsize{k}} \ – \overline{y} ) \\[ 10pt ]
&\text{ただし、} \\[ 5pt ]
&\text{$x_{\scriptsize{1}} \ , \ x_{\scriptsize{2}} \ , \cdots \cdots , \ x_{\scriptsize{n}}$ :変量 $x$ におけるデータの値} \\[ 5pt ]
&\text{$y_{\scriptsize{1}} \ , \ y_{\scriptsize{2}} \ , \cdots \cdots , \ y_{\scriptsize{n}}$ :変量 $y$ におけるデータの値} \\[ 5pt ]
&\text{$\overline{x}$ :変量 $x$ の平均値} \\[ 5pt ]
&\text{$\overline{y}$ :変量 $y$ の平均値} \\[ 5pt ]
&\text{$x_{\scriptsize{1}} \ – \overline{x} \ , \ x_{\scriptsize{2}} \ – \overline{x} \ , \cdots \cdots , \ x_{\scriptsize{n}} \ – \overline{x}$ :変量 $x$ の偏差} \\[ 5pt ]
&\text{$y_{\scriptsize{1}} \ – \overline{y} \ , \ y_{\scriptsize{2}} \ – \overline{y} \ , \cdots \cdots , \ y_{\scriptsize{n}} \ – \overline{y}$ :変量 $y$ の偏差}
\end{align*}
相関係数
散布図によって相関の傾向を読み取ることができますが、より詳しく傾向を知りたければ数量を求める必要があります。
2つの変量の相関関係の強弱をみる量として相関係数があります。相関係数は以下のように表されます。
相関係数
\begin{align*}
&\text{$x \ , \ y$ の標準偏差、共分散をそれぞれ} \\[ 5pt ]
&\quad s_{\scriptsize{x}} \ , \ s_{\scriptsize{y}} \ , \ s_{\scriptsize{xy}} \\[ 7pt ]
&\text{とする。} \\[ 5pt ]
&\text{このとき、相関係数 $r$ は} \\[ 5pt ]
&\quad r = \frac{s_{\scriptsize{xy}}}{s_{\scriptsize{x}} \ s_{\scriptsize{y}}} \\[ 7pt ]
&\text{と表される。}
\end{align*}
これをデータの各値や平均値を用いて表すと以下のようになります。
相関係数
\begin{align*}
\quad r &= \frac{s_{\scriptsize{xy}}}{s_{\scriptsize{x}} \ s_{\scriptsize{y}}} \\[ 10pt ]
&= \frac{\frac{1}{n} \left\{( x_{\scriptsize{1}} \ – \overline{x} ) ( y_{\scriptsize{1}} \ – \overline{y} ) + ( x_{\scriptsize{2}} \ – \overline{x} ) ( y_{\scriptsize{2}} \ – \overline{y} ) + \cdots + ( x_{\scriptsize{n}} \ – \overline{x} ) ( y_{\scriptsize{n}} \ – \overline{y} ) \right\}}{\sqrt{\frac{1}{n} \left\{( x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + ( x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots + ( x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\}} \ \sqrt{\frac{1}{n} \left\{ ( y_{\scriptsize{1}} \ – \overline{y} )^{\scriptsize{2}} + ( y_{\scriptsize{2}} \ – \overline{y} )^{\scriptsize{2}} + \cdots + ( y_{\scriptsize{n}} \ – \overline{y} )^{\scriptsize{2}} \right\}}} \\[ 10pt ]
&= \frac{( x_{\scriptsize{1}} \ – \overline{x} ) ( y_{\scriptsize{1}} \ – \overline{y} ) + ( x_{\scriptsize{2}} \ – \overline{x} ) ( y_{\scriptsize{2}} \ – \overline{y} ) + \cdots + ( x_{\scriptsize{n}} \ – \overline{x} ) ( y_{\scriptsize{n}} \ – \overline{y} )}{\sqrt{ \left\{ ( x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + ( x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots + ( x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\} \left\{( y_{\scriptsize{1}} \ – \overline{y} )^{\scriptsize{2}} + ( y_{\scriptsize{2}} \ – \overline{y} )^{\scriptsize{2}} + \cdots + ( y_{\scriptsize{n}} \ – \overline{y} )^{\scriptsize{2}} \right\} }}
\end{align*}
この相関係数は-1≦r≦1の範囲の値となります。また、相関係数の値によって相関の強弱が分かります。
相関の強弱
- rの値が1に近いとき、正の相関が強い。
- rの値が0に近いとき、直線的な相関関係はない。
- rの値が-1に近いとき、負の相関が強い。
共分散と相関係数の関係
相関係数において、分母は標準偏差の積なので、つねに正の値です。ですから、相関係数の正負は、分子の共分散によって決まります。
共分散は、xの偏差とyの偏差との積の平均値でした。
共分散
共分散を $s_{\scriptsize{xy}}$ とすると
\begin{align*}
&\quad s_{\scriptsize{xy}} = \frac{1}{n} \left\{ ( x_{\scriptsize{1}} \ – \overline{x} ) ( y_{\scriptsize{1}} \ – \overline{y} ) + ( x_{\scriptsize{2}} \ – \overline{x} ) ( y_{\scriptsize{2}} \ – \overline{y} ) + \cdots \cdots + ( x_{\scriptsize{n}} \ – \overline{x} ) ( y_{\scriptsize{n}} \ – \overline{y} ) \right\} \\[ 10pt ]
&\text{または} \\[ 5pt ]
&\quad s_{\scriptsize{xy}} = \frac{1}{n} \displaystyle \sum_{ k = 1 }^{ n } ( x_{\scriptsize{k}} \ – \overline{x} ) ( y_{\scriptsize{k}} \ – \overline{y} )
\end{align*}
共分散の正負については、計算して調べても良いのですが、散布図で点の分布を見ればある程度分かります。
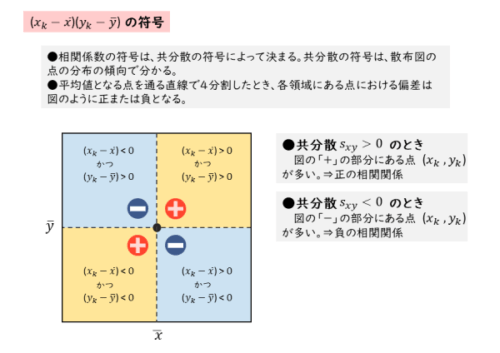
散布図において、平均値を座標とする点 $(\overline{x} \ , \ \overline{y})$ を通る直線で座標平面を4分割します(下図参照)。
この直線が点 $( x_{\scriptsize{k}} \ , \ y_{\scriptsize{k}} )$ における偏差の積 $( x_{\scriptsize{k}} \ – \overline{x} )( y_{\scriptsize{k}} \ – \overline{y} )$ の正負を決める境界になります。
 偏差の積の符号と共分散
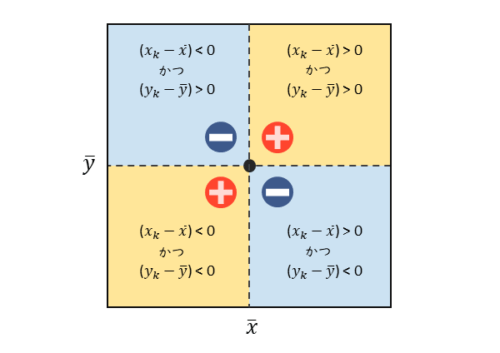
偏差の積の符号と共分散 偏差の積 $( x_{\scriptsize{k}} \ – \overline{x} )( y_{\scriptsize{k}} \ – \overline{y} )$ の符号は図のようになります。
 偏差の積の符号
偏差の積の符号 4分割した領域において、各点における偏差の正負は以下のようになります。
各領域における偏差の正負
- 右上の領域(+の部分):x,yの偏差がともに正となる点が分布。偏差の積は正の値。
- 左下の領域(+の部分):x,yの偏差がともに負となる点が分布。偏差の積は正の値。
- 右下の領域(-の部分):xの偏差が正、yの偏差が負となる点が分布。偏差の積は負の値。
- 左上の領域(-の部分):xの偏差が負、yの偏差が正となる点が分布。偏差の積は負の値。
以上のことから、+の部分の領域に点が多く分布すれば、偏差の積 $( x_{\scriptsize{k}} \ – \overline{x} )( y_{\scriptsize{k}} \ – \overline{y} )$ が正の値となるような点 $( x_{\scriptsize{k}} \ , \ y_{\scriptsize{k}} )$ が多くなるので、共分散が正の値となります。
+の部分の領域に点が多く分布するということは、正の相関関係が見られることも分かります。
また、-の部分の領域に点が多く分布すれば、偏差の積 $( x_{\scriptsize{k}} \ – \overline{x} )( y_{\scriptsize{k}} \ – \overline{y} )$ が負の値となるような点 $( x_{\scriptsize{k}} \ , \ y_{\scriptsize{k}} )$ が多くなるので、共分散が負の値となります。
-の部分の領域に点が多く分布するということは、負の相関関係が見られることも分かります。
共分散、相関係数、相関関係の関係
- 共分散sxy>0 ⇔ 相関係数r>0 ⇔ 正の相関関係
- 共分散sxy<0 ⇔ 相関係数r<0 ⇔ 負の相関関係
散布図を見て、共分散や相関係数の正負や、2つの変量の間の相関関係を読み取れるようにしておきましょう。
次は共分散や相関係数などを扱った問題を実際に解いてみましょう。