図形と方程式|垂線の長さの最小について

今回は、垂線の長さの最小について学習しましょう。折れ線の長さもそうでしたが、既習内容を総動員して考える単元です。
点の座標や直線の方程式などをすぐに求めることができるでしょうか。また、図形を扱うので、作図できないと難易度が上がります。例題や練習問題を通じて訓練しましょう。
垂線の長さ
最短経路は垂線
共有点を持たない2つのグラフを考えます。
たとえば、放物線と直線のグラフです。各グラフ上に点があり、その2点間の距離が最小になるときを考えます。
ただし、2点は各グラフ上にあるだけでまだ座標が決まっていません。
仮に、2点の座標を自分で定義しても、変数の個数から2点間の距離を求めても上手くいきそうにありません。
図形的に考えて、どのような場合に2点間の距離が最小になるのかを考えてみましょう。
距離とは、最短経路の長さのことです。2点間の距離であれば、最短経路は2点を結ぶ線分の長さとなります。
一般に、図形の高さのように、最短経路が垂線となることが多いので、距離と言えば「垂線」をイメージすると良いでしょう。
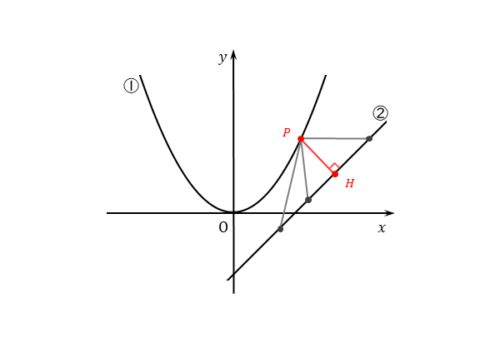
図から分かるように、放物線①上の点を固定して考えると、2点間の距離が最小となるのは、2点を結ぶ線分が直線②に対して垂線になっているときです。
まずは、長さを最小にするには、直線に対する垂線であればよいことを理解しましょう。
最短経路=垂線
最短の垂線は平行線を活用
しかし、放物線①上の点の位置が変わると、同じ垂線であっても2点間の距離が短くなったり、長くなったりします。垂線の中から、その長さが最小となるものを探さなければなりません。
垂線の長さが最小となるのは、放物線①上の点のうち、直線②に最も近い点での垂線です。直線②に最も近い点は、直線②の平行線を利用すると見つかります。
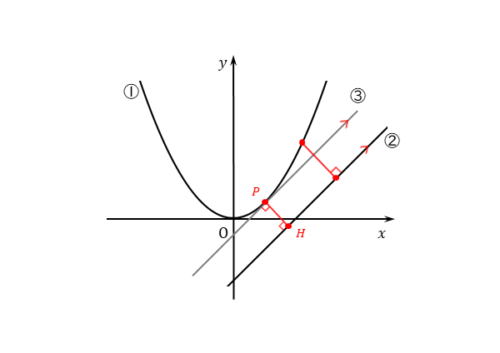
放物線①上にあり、平行線③上にもある点は、放物線①と平行線③の接点です。この接点を通る垂線の長さが、垂線の中でも最小となります。
放物線と直線の平行線との接点からの垂線=2点間の最短経路
以上のことから、2点間の距離が最小となるには、放物線①上の点のうち直線②に最も近い点と、直線②との距離を考えればよいことが分かります。ですから、点と直線の距離の式を覚えていることが前提となります。
点と直線の距離
点 $(x_{1} \ , \ y_{1})$ と直線 $ax+by+c=0$ の距離 $d$
\begin{align*} \quad d=\frac{| ax_{1}+by_{1}+c |}{\sqrt{a^{2}+b^{2}}} \end{align*}垂線の長さの最小を求めてみよう
垂線の長さが最小となるときを考えてみましょう。
例題
放物線 $y=x^{2} \ \cdots$ ①と直線 $y=x-1 \ \cdots$ ②がある。
直線②上の点で、放物線①との距離が最小となる点の座標と、その距離の最小値を求めよ。
「放物線との距離が最小となるような、直線上の点の座標を求めよ」と指示されています。問題文の指示に素直に従って、直線上の点から放物線への距離を考えたり、直線上の点の座標を定義したりするかもしれません。
そのように考えてしまうと、点と直線の距離に結びつかない可能性があります。点と直線の距離は、直線上にない点からの距離で、直線上にある点では使えないからです。
しかし、この問題文の意図が上で解説した内容であることが分かっていれば、点と直線の距離を利用する方針を立てることができるはずです。
直線上の点からの距離ではなく、放物線上の点からの距離で考える。
例題の解答・解説
作図すると、以下の通りです。
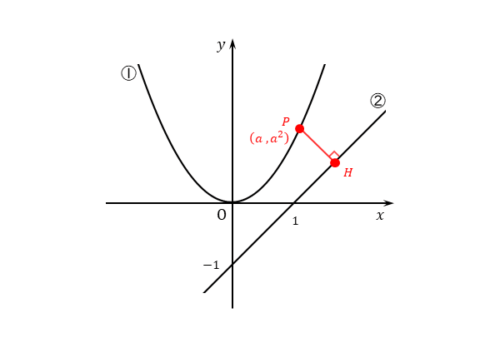
この例題では、直線②上の点ではなく、放物線①上の点の座標を定義します。ここが一番難しいかもしれません。
放物線①上の点を定義したら、点と直線の距離を利用します。
例題の解答例 1⃣
放物線①上の点を $P (a \ , \ a^{2} )$ とする。
また、②より
\begin{align*} \quad x-y-1=0 \end{align*}点 $P$ から直線②に引いた垂線を $PH$ とすると
\begin{align*} \quad PH=\frac{| a-a^{2}-1 |}{\sqrt{1^{2}+(-1)^{2}}} \end{align*}よって
\begin{align*} \quad PH=\frac{| a^{2}-a+1 |}{\sqrt{2}} \end{align*}放物線②上の点Pから下した垂線 PH の長さを導くことができました。ただし、PHは点Pのx座標aについての2次式で表されます。このことから、PHはaの2次関数であることが分かります。
PHの値は、2次関数的に変化するので、2次式によっては最小値を求めることができます。PHの右辺を平方完成します。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad PH=\frac{| a^{2}-a+1 |}{\sqrt{2}} \end{align*}これの右辺を変形すると
\begin{align*} \quad PH=\frac{1}{\sqrt{2}} \left| \ \left(a-\frac{1}{2} \right)^{2}+\frac{3}{4} \ \right| \end{align*}このままでも解き進めていくことはできますが、もう少し変形しておきます。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad PH=\frac{1}{\sqrt{2}} \left| \ \left(a-\frac{1}{2} \right)^{2}+\frac{3}{4} \ \right| \end{align*}ここで
\begin{align*} \quad \left(a-\frac{1}{2} \right)^{2} \geqq 0 \end{align*}であるので
\begin{align*} \quad \left(a-\frac{1}{2} \right)^{2}+\frac{3}{4} \gt 0 \end{align*}よって
\begin{align*} \quad PH=\frac{1}{\sqrt{2}} \left\{ \left(a-\frac{1}{2} \right)^{2}+\frac{3}{4} \right\} \end{align*}すなわち
\begin{align*} \quad PH=\frac{1}{\sqrt{2}} \left(a-\frac{1}{2} \right)^{2}+\frac{3 \sqrt{2}}{8} \end{align*}絶対値の中の2次式を平方完成すると、式の値がつねに正であることが分かります。式の値がつねに正であることから、絶対値を外すことができます。
PHの最小値と、そのときのaの値を求めます。このときの点Pは、直線②に最も近い点です。
例題の解答例 4⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad PH=\frac{1}{\sqrt{2}} \left(a-\frac{1}{2} \right)^{2}+\frac{3 \sqrt{2}}{8} \end{align*}よって、$PH$ は $a=\frac{1}{2}$ で最小値 $\frac{3 \sqrt{2}}{8}$をとる。
このときの直線PHの方程式を求めます。
例題の解答例 5⃣
\begin{align*} \quad \vdots \end{align*}$a=\frac{1}{2}$ のとき、点 $P$ の座標は
\begin{align*} \quad P \left( \frac{1}{2} \ , \ \frac{1}{4} \right) \end{align*}となるので、直線 $PH$ の方程式は
\begin{align*} \quad -1 \cdot \left(x-\frac{1}{2} \right)-1 \cdot \left(y-\frac{1}{4} \right)=0 \end{align*}整理すると
\begin{align*} \quad 4x+4y-3=0 \quad \cdots \text{③} \end{align*}一般形で表した垂直な直線の方程式を利用して、直線PHの方程式を求めています。
もとにする直線の方程式と1点の座標が分かっていれば、わざわざ傾きを求める必要がないのでとても便利です。
垂直な直線の方程式
点 $(x_{1} \ , \ y_{1})$ を通り、直線 $ax+by+c=0$ に垂直な直線の方程式は
\begin{align*} \quad b \left( x-x_{1} \right)-a \left( y-y_{1} \right)=0 \end{align*}これは $a=0$ または $b=0$ の場合も成り立つ。
直線②と直線PHの交点が点Hとなります。点Hの座標を求めます。
例題の解答例 6⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 4x+4y-3=0 \quad \cdots \text{③} \end{align*}点 $H$ の座標は②,③を連立して解くと
\begin{align*} \quad x=\frac{7}{8} \ , \ y=-\frac{1}{8} \end{align*}したがって、求める点の座標は
\begin{align*} \quad \left( \frac{7}{8} \ , \ -\frac{1}{8} \right) \end{align*}また、距離の最小値は
\begin{align*} \quad \frac{3\sqrt{2}}{8} \end{align*}少し過程が長くなったので、手順を確認しましょう。
垂線の長さの最小を求める手順
- 円と直線が異なる2点で交わる=円と直線が2個の共有点をもつ
- 円と直線が1点で接する=円と直線が1個の共有点をもつ
- 円と直線が交わらない=円と直線が共有点をもたない放物線上の点を定義する。
- この点と直線の距離を求める。
- 距離の右辺(2次式)を平方完成する。
- 3から距離の最小値と、定義した点のx座標が分かる。
- y座標を求めると、1で定義した点の座標が決まる。
- 5の点を通り、直線に垂直な直線の方程式を求める。
- 2直線の交点の座標を求める。
ここで注意したいのは、1番目の放物線上の点の定義です。問題文に惑わされて、直線上の点を定義しないように気を付けましょう。
次は、垂線の長さの最小を扱った問題を実際に解いてみましょう。










