図形と方程式|2直線の交点を通る直線について

今回は、2直線の交点を通る直線について学習しましょう。この単元では、とても便利な方程式が出てきます。なお、これと同様の式があとの単元でも出てきます。
直線の方程式と直線上にある点の座標との関係を理解していればそれほど難しく感じません。不安のある人はこれまでに学習した内容を確認しながら取り組みましょう。
2直線の交点を通る直線
2点を通る直線の方程式の求め方
2直線の方程式が与えられ、それらの交点と他の1点を通る直線の方程式を求めるとします。このとき、以下の手順で求めるのがこれまでの解法です。
2直線の交点と他の1点を通る直線の方程式の求め方
- 2直線の方程式を連立して解いて、2直線の交点の座標を求める。
- 2点(交点と他の1点)を通る直線の方程式(公式)を利用して求める。
なお、2点を通る直線の方程式は以下の通りです。きちんと覚えておきましょう。
2点を通る直線の方程式
異なる $2$ 点
\begin{align*} \quad (x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2}) \end{align*}を通る直線の方程式は
$[1] \ x_{1} \neq x_{2}$ のとき
\begin{align*} \quad y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \left(x-x_{1} \right) \end{align*}$[2] \ x_{1}=x_{2}$ のとき
\begin{align*} \quad x=x_{1} \end{align*}$[1] \ , \ [2]$ の両方を満たす式
\begin{align*} \quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}[1],[2]の両方を満たす式を使えるようになると便利です。
2直線の交点を通る直線の方程式
これまでの解法であれば、上述のような手順で進めていきますが、ここでは違った視点から直線の方程式を求めます。
2直線の交点は、両方の直線上にある点です。直線上にある点の座標は、その直線の方程式の解でした。したがって、交点の座標は、2直線の方程式、つまり連立方程式の解となります。ここがこの単元の要点です。
これまでであれば、2直線の方程式を連立していましたが、これを1つの方程式で表すことを考えてみましょう。
2直線の交点を通る直線の方程式は、以下のように表せます。
2点を通る直線の方程式
交わる $2$ 直線
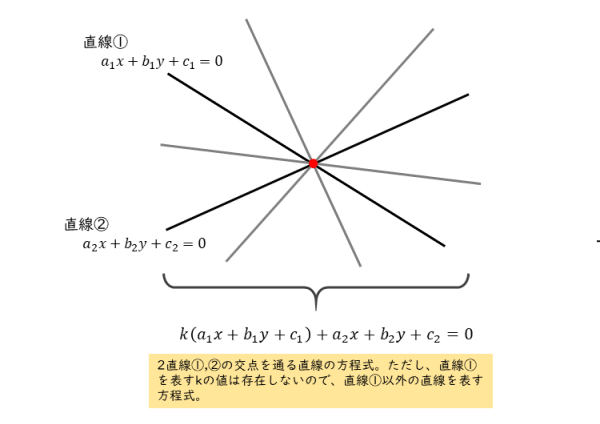
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}に対し、$k$ を定数とする。
このとき、$2$ 直線の交点を通る直線の方程式は
\begin{align*} \quad k \left(a_{1}x+b_{1}y+c_{1} \right)+\left(a_{2}x+b_{2}y+c_{2} \right)=0 \end{align*}と表せる。
なぜ、上述の方程式が、2直線の交点を通る方程式となるのかを考えてみましょう。
2点を通る直線の方程式の確認
交わる $2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \quad \cdots \text{①} \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \quad \cdots \text{②} \end{align*}に対し、$k$ を定数とする。
このとき、$2$ 直線の交点を通る直線の方程式は
\begin{align*} \quad k \left(a_{1}x+b_{1}y+c_{1} \right)+\left(a_{2}x+b_{2}y+c_{2} \right)=0 \quad \cdots \text{③} \end{align*}$2$ 直線①,②の交点を $p$ とし、その座標を
\begin{align*} \quad P \ (\alpha \ , \ \beta) \end{align*}とすると、直線①,②上の点であるので
\begin{align*} &\quad a_{1} \alpha+b_{1} \beta+c_{1}=0 \\[ 7pt ] &\quad a_{2} \alpha+b_{2} \beta+c_{2}=0 \end{align*}が成り立つ。
ところで、方程式③は
\begin{align*} \quad \left(k a_{1}+a_{2} \right)x+\left(k b_{1}+b_{2} \right)y+\left(k c_{1}+c_{2} \right)=0 \end{align*}の形になるので、直線を表す。
また、方程式③に点 $P \ (\alpha \ , \ \beta)$ の座標を代入すると
\begin{align*} \quad k \left(a_{1} \alpha+b_{1} \beta+c_{1} \right)+\left(a_{2} \alpha+b_{2} \beta+c_{2} \right)=0 \end{align*}が成り立つので、$x=\alpha \ , \ y=\beta$ は方程式③の解である。
したがって、直線③は交点 $P \ (\alpha \ , \ \beta)$ を通る直線の方程式である。
ただし、直線①を表す $k$ の値は存在しない。
交点を通る直線の方程式は無数に存在します。直線の方程式が決まるには、少なくとも2点が必要です。交点を通る直線の候補を表すのが直線③の方程式です。
直線③の方程式では、2直線①,②上の交点以外の点の座標を代入しても等式が成り立ちません。定数kの値が定まっていないからです。
等式が成り立つのは、2直線①,②の交点の座標を代入したときだけです。ですから、直線③の方程式が交点の座標を解にもつ、言い換えると直線③は2直線①,②の交点を通ることだけは確実に言えるわけです。
2直線の交点を通る直線の方程式は、定数kを用いて一般化された形で表されます。なお、特定の直線の方程式は、定数kの値が定まることによって得られます。定数kの値が決まるのは、他の1点の座標が与えられたときです。
2直線の交点を通る直線の方程式を求める手順
- 2直線の交点を通る直線の方程式を考える。(定数kを用いて表す)
- 他の1点の座標を利用して、定数kの値を定める。
2変数で表される式の表し方
直線の方程式には、x,yの2つの変数が用いられています。このような式を以下のように表すことがあります。
2変数で表される式の表し方
一般に、変数 $x \ , \ y$ で表される式を
\begin{align*} \quad f (x \ , \ y) \end{align*}などと表す。
たとえば、直線の方程式であれば
\begin{align*} &\quad f (x \ , \ y)=0 \\[ 7pt ] &\quad g (x \ , \ y)=0 \end{align*}などと表す。
このような表し方を利用すると、2直線の交点を通る直線は以下のように表せます。
2直線の交点を通る直線の方程式
次の $2$ 直線
\begin{align*} &\quad f(x \ , \ y)=0 \\[ 7pt ] &\quad g(x \ , \ y)=0 \end{align*}の交点を通る直線は、$k$ を定数とすると
\begin{align*} \quad kf (x \ , \ y)+g (x \ , \ y)=0 \end{align*}と表せる。
直線の方程式をそのまま使うよりも簡潔に記述できます。また、たとえば円などの直線以外の図形も方程式で表されますが、同じようにこの表し方を用いることができます。
方程式が複雑であればあるほど、この表し方の良さが発揮されますが、直線の方程式くらいではあまり感じられないかもしれません。
2直線の交点を通る直線の方程式を求めてみよう
次の例題を考えてみましょう。
例題
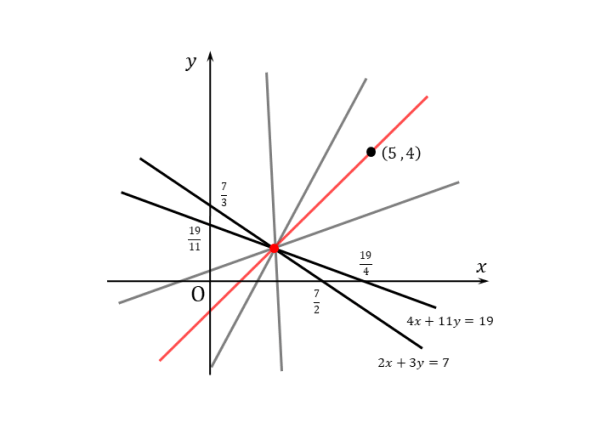
次の $2$ 直線
\begin{align*} &\quad 2x+3y=7 \quad \cdots \text{①} \\[ 7pt ] &\quad 4x+11y=19 \quad \cdots \text{②} \end{align*}の交点を通り、点 $(5 \ , \ 4)$ を通る直線の方程式を求めよ。
例題の解答・解説
まず、2直線①,②の交点を通る直線を導きます。ただし、与えられた2直線の方程式が、中途半端な形になっているので注意しましょう。一般形で用いるので、「~=0」の形に変形しましょう。
例題の解答例 1⃣
$k$ を定数とすると
\begin{align*} \quad k \left(2x+3y-7 \right)+\left(4x+11y-19 \right)=0 \quad \cdots \text{③} \end{align*}は、直線①,②の交点を通る直線を表す。
定数kの値が定まっていないので、2直線①,②の交点を通る直線はいくつもある状態です。
問題では、他の1点の座標が与えられているので、直線の方程式を決定することができます。
他の1点の座標は、求めたい直線の方程式の解でなければなりません。ですから、座標を③式に代入したとき、等式が成り立たなければなりません。これによって、定数kの値が決まります。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad k \left(2x+3y-7 \right)+\left(4x+11y-19 \right)=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \end{align*}直線③が点 $(5 \ , \ 4)$ を通るとすると、方程式③に $x=5 \ , \ y=4$ を代入して
\begin{align*} &\quad k \left(2 \cdot 5+3 \cdot 4-7 \right)+\left(4 \cdot 5+11 \cdot 4-19 \right)=0 \\[ 7pt ] &\quad 15k+45=0 \end{align*}これを解くと
\begin{align*} \quad k=-3 \end{align*}定数kの値が定まりました。k=-3のとき、点(5,4)の座標を③式に代入すると、等式が成り立ちます。このことは、点(5,4)の座標を代入したとき、等式が成り立つ定数kの値を求めたので明らかです。
求めたkの値を③式に代入して、交点と点(5,4)を通る直線の方程式を求めます。
例題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad k \left(2x+3y-7 \right)+\left(4x+11y-19 \right)=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad k=-3 \end{align*}これを③に代入すると
\begin{align*} \quad -3 \left(2x+3y-7 \right)+\left(4x+11y-19 \right)=0 \end{align*}整理すると
\begin{align*} \quad x-y-1=0 \end{align*}得られた直線の方程式に、交点や点(5,4)の座標を代入してみましょう。
等式が成り立つので、交点や点(5,4)の座標がちゃんと方程式の解になっています。このことから、得られた直線は、交点や点(5,4)を通ることが分かります。
この解法では「2直線の交点の座標を求めなくて良い」ことが最大の利点です。計算量が連立方程式を解くよりも少なくて済むので、積極的に利用したい解法です。
例題の別解・解説
これまでの知識で解くと、以下の通りです。
例題の別解例
\begin{align*} &\quad 2x+3y=7 \quad \cdots \text{①} \\[ 7pt ] &\quad 4x+11y=19 \quad \cdots \text{②} \end{align*}$2$ 直線の交点の座標は①,②を連立して
①×2-②
\begin{align*} \quad y=1 \end{align*}これと①より
\begin{align*} \quad x=2 \end{align*}よって、$2$ 点 $(2 \ , \ 1) \ , \ (5 \ , \ 4)$ を通る直線の方程式は
\begin{align*} &\quad \left(4-1 \right) \left(x-2 \right)-\left(5-2 \right) \left(y-1 \right)=0 \\[ 7pt ] &\quad 3 \left(x-2 \right)-3 \left(y-1 \right)=0 \end{align*}したがって
\begin{align*} \quad x-y-1=0 \end{align*}別解の方が素直な解法ではありますが、計算量が多くなります。
次は、2直線の交点を通る直線を扱った問題を実際に解いてみましょう。