図形と方程式|2つの円の位置関係について

2つの円の位置関係を扱った問題を解いてみよう
次の問を解いてみましょう。
問
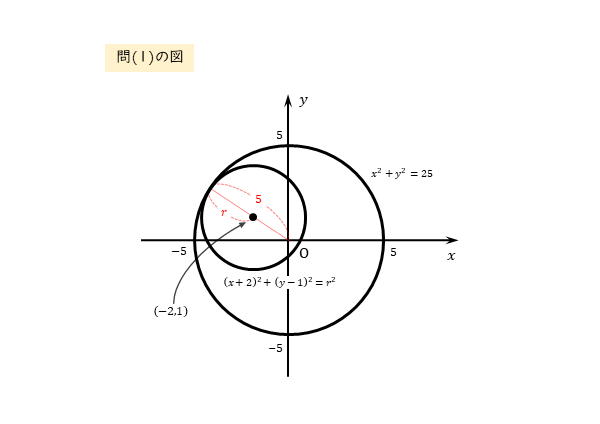
$(1)$ 中心が $(-2 \ , \ 1)$ で、円 $x^{2}+y^{2}=25$ に内接する円の方程式を求めよ。
$(2)$ $2$ つの円 $x^{2}+y^{2}=r^{2} \ (r \gt 0)$ … ①,$x^{2}+y^{2}-6x+8y+16=0$ … ②が共有点をもつような $r$ の値の範囲を求めよ。
問(1)の解答・解説
問(1)
中心が $(-2 \ , \ 1)$ で、円 $x^{2}+y^{2}=25$ に内接する円の方程式を求めよ。
問(1)は、「外接する」が「内接する」に変わっただけで、例題(1)と同様の方針で解くことができます。
求める円の方程式を予め準備しておきます。
問(1)の解答例 1⃣
求める円の方程式を
\begin{align*} \quad \left(x+2 \right)^{2}+\left(y-1 \right)^{2}=r^{2} \ \cdots \ \text{①} \end{align*}とおく。
ここで、円が内接するための条件を考えます。言い換えると、求める半径rの条件です。
問(1)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left(x+2 \right)^{2}+\left(y-1 \right)^{2}=r^{2} \ \cdots \ \text{①} \\[ 7pt ] &\quad \vdots \end{align*}円①が円 $x^{2}+y^{2}=25$ …②に内接するので
\begin{align*} \quad \sqrt{ \left(-2 \right)^{2} + 1^{2} } = \left| 5-r \right| \end{align*}が成り立つ。
ここで、$0 \lt r \lt 5$ より
\begin{align*} \quad \sqrt{ \left(-2 \right)^{2} + 1^{2} } = 5-r \end{align*}よって
\begin{align*} \quad \sqrt{5} = 5-r \end{align*}2つの円が内接するには、2つの円の中心の位置関係を考慮すると、円①の半径が円②の半径よりも小さくなければなりません。
また、中心間の距離は、2つの円の半径の差に等しくなります。この条件から得られるのが半径rについての一次方程式です。ただし、内接するときの方程式では、絶対値を外すために半径rの条件(0<r<5)が必要になるので注意しましょう。
半径rについての方程式を導出できたので、これを解きます。
問(1)の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \sqrt{5} = 5-r \end{align*}これを解くと
\begin{align*} \quad r=5-\sqrt{5} \end{align*}①より、求める円の方程式は
\begin{align*} \quad \left(x+2 \right)^{2}+\left(y-1 \right)^{2}=\left(5-\sqrt{5} \right)^{2} \end{align*}得られた半径rの値は、円②の半径よりも小さくなっていることが分かります。
また、半径rについての方程式は、簡単な一次方程式なので、きちんと条件から立式できるようにしましょう。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とする。
$2$ つの円が内接するか、一致するとき
\begin{align*} \quad d=\left| r-r’ \right| \end{align*}を満たす。
問(1)の別解例
解答例2⃣で半径rの条件を挙げて解きましたが、条件を挙げずに解くこともできます。
問(1)の別解例
求める円の方程式を
\begin{align*} \quad \left(x+2 \right)^{2}+\left(y-1 \right)^{2}=r^{2} \ \cdots \ \text{①} \end{align*}とおく。
円①が円 $x^{2}+y^{2}=25$ …①に内接するので
\begin{align*} \quad \sqrt{ \left(-2 \right)^{2} + 1^{2} } = \left| 5-r \right| \end{align*}が成り立つ。
これを整理すると
\begin{align*} \quad \left| 5-r \right| = \sqrt{5} \end{align*}さらに
\begin{align*} \quad 5-r = \pm \sqrt{5} \end{align*}よって
\begin{align*} \quad r = 5 \pm \sqrt{5} \end{align*}ここで、$0 \lt r \lt 5$ より
\begin{align*} \quad r = 5 – \sqrt{5} \end{align*}①より、求める円の方程式は
\begin{align*} \quad \left(x+2 \right)^{2}+\left(y-1 \right)^{2}=\left(5-\sqrt{5} \right)^{2} \end{align*}半径rの条件を考えずに、絶対値の性質を利用して絶対値を外し、方程式を解いています。解を求めることはできるのですが、どちらがスマートかと言えば、半径rの条件を先に挙げた解答例の方でしょう。
また、別解例でも最後に吟味しなければなりません。しかも、与えられたr>0の条件だけではどちらの解が適しているかを判断できません。
円①の半径が、円②の半径よりも小さい(r<5)という、隠された条件に気付けるかどうかがポイントです。2つの円が内接するときは、半径rの条件に気を付けましょう。
2つの円が内接するときの半径rの条件に注意しよう。
問(2)の解答・解説
問(2)
$2$ つの円 $x^{2}+y^{2}=r^{2} \ (r \gt 0)$ … ①,$x^{2}+y^{2}-6x+8y+16=0$ … ②が共有点をもつような $r$ の値の範囲を求めよ。
問(2)は、例題(2)と同様の問題です。2つの円が共有点をもつのは1個のときと、2個のときがあるので注意しましょう。
円②の方程式を変形して、中心と半径を求めておきます。
問(2)の解答例 1⃣
円①の中心は点 $(0 \ , \ 0)$ で半径は $r$ である。
また、円②の方程式を変形すると
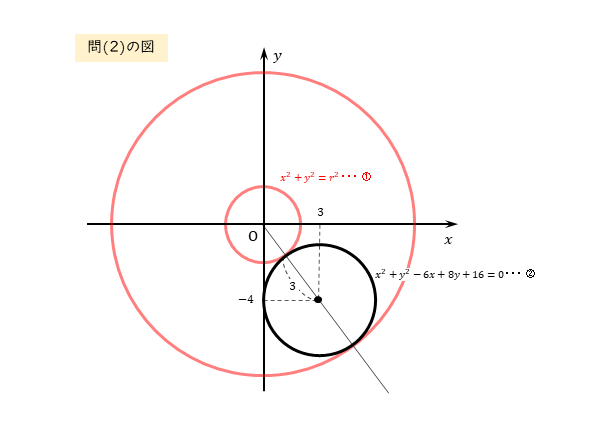
\begin{align*} &\quad x^{2}+y^{2}-6x+8y+16=0 \\[ 7pt ] &\quad \left(x-3 \right)^{2}+\left(y+4 \right)^{2}=9 \end{align*}となるので、中心は点 $(3 \ , \ -4)$ で半径は $3$ である。
2つの円の中心と半径がそれぞれ分かったので作図しておきます。
2つの円が共有点をもつ状況をイメージできるように、円①を複数描いておきます。
ここでは、外接するとき、内接するときの2パターンを描いています。
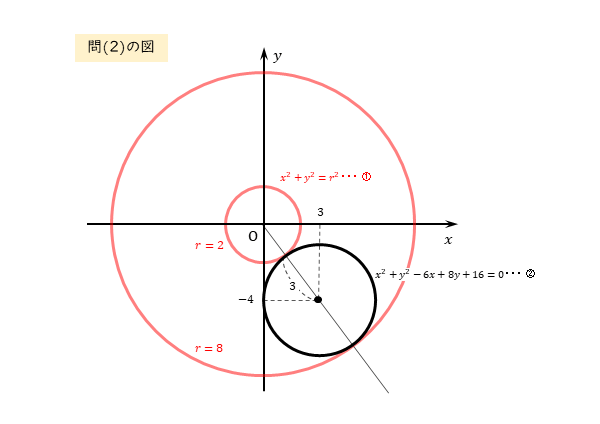
図から、2つの円が共有点をもつのは、内接するときから外接するときまでです。
2つの円の中心間の距離を求めます。
問(2)の解答例 2⃣
$2$ つの円の中心間の距離は
\begin{align*} \quad \sqrt{ 3^{2} + \left(-4 \right)^{2} } &= \sqrt{ 25 } \\[ 7pt ] &= 5 \end{align*}2つの円の半径と中心間の距離が揃ったので、2つの円が共有点をもつときの関係式を利用して、半径rについての不等式を導出します。
問(2)の解答例 3⃣
$2$ つの円①,②が共有点をもつ条件は
\begin{align*} \quad \left| r-3 \right| \leqq 5 \leqq r+3 \end{align*}$\left| r-3 \right| \leqq 5$ から
\begin{align*} \quad -5 \leqq r-3 \leqq 5 \end{align*}よって
\begin{align*} \quad -2 \leqq r \leqq 8 \ \cdots \ \text{③} \end{align*}$5 \leqq r+3$ から
\begin{align*} \quad 2 \leqq r \ \cdots \ \text{④} \end{align*}③,④と $r \gt 0$ から共通範囲を求めると
\begin{align*} \quad 2 \leqq r \leqq 8 \end{align*}作図をすれば分かりますが、図形的に解くこともできます。検算にもなるので、作図する習慣を付けましょう。
2つの円が共有点をもつのは、内接するときから外接するときまでの範囲。
例題や問を通して注意したいのは、2つの円が外接するときを除いて、求めたい半径rについての方程式や不等式に絶対値が含まれることです。
立式することはそれほど難しくありませんが、絶対値の扱いを間違えると大変なことになります。方程式や不等式を解くときに躓かないように、絶対値の扱いをしっかりマスターしておきましょう。
2つの円の位置関係
半径がそれぞれ $r \ , \ r’$ である円の中心間の距離を $d$ とする。
$2$ つの円が共有点をもつとき
\begin{align*} \quad \left| r-r’ \right| \leqq d \leqq r+r’ \end{align*}を満たす。
Recommended books
大学進学を考えたとき、記述を重視した学習を日常的に行った方が良いでしょう。試験の難易度は、マーク形式よりも記述形式の方が高いからです。
また、記述では思考力や表現力などが必要で、それらを身に付けるのは一朝一夕には難しいことも理由の1つです。
記述の訓練は、基本的に教科書や参考書の例題を真似することから始まりますが、記号の使い分けや独特の表現などがあり、手探りで進めていくのは大変です。
そこでお勧めしたいのが以下の2冊です。記述の訓練に特化したテキストになります。
オススメその1
1冊目は『基礎からのジャンプアップノート 数学 記述式答案 書き方ドリル』で、数学に苦手意識のある人におすすめです。
数学Ⅰ+A+Ⅱ+Bの記述力の基礎力を固めるなら、まずはこのドリルから!!
問題編64ページ、別冊解答編32ページ
- 証明問題、場合分けの答案の書き方のコツがわかる
- 「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい
- 「例(手本)」→「Check!」→「練習問題」 まねる&繰り返すの流れで、記述力UP!
- 別冊「解答編」では、練習問題をくわしく解答
『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。
オススメその2
2冊目は『総合的研究 記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。
『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。
この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。
ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。
(中略)数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です(抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です)。
自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。
この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。
それでは、《伝える》レッスンをはじめましょう!(まえがきより)
著者が異なりますが、こちらも『総合的研究』シリーズです。
さいごにもう一度まとめ
- 2つの円の中心と半径をそれぞれ確認しよう。
- 2つの円の中心から、中心間の距離を求めよう。
- 2つの円が外接するとき、中心間の距離は半径の和に等しい。
- 2つの円が内接するとき、中心間の距離は半径の差(絶対値記号を忘れない)に等しい。
- 2つの円が内接するとき、半径の条件に注意しよう。
- 2つの円が共有点をもつのは、2つの円が内接するときから外接するときまで。
- 絶対値の扱いに注意しよう。