積分法|定積分と不等式の証明について

答案を推敲しよう
かなり長くなってしまった答案ですが、実際の答案ではどの程度の記述に留めれば良いでしょうか?
教科書や問題集などの模範解答を参考にするのが一番の近道です。慣れてきたら、自分の答案と模範解答を比べたり、採点者がどんな答案を書いてほしいかを自分なりに考えてみたりすると良いでしょう。より客観的な視点が身に付きます。
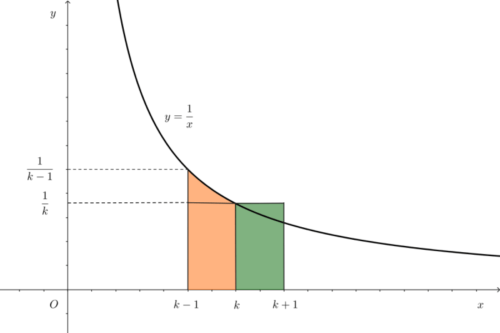
推敲したあとの記述例は以下のようになります。また、答案に図があると説明しやすくなります。
問の記述例
解答例では計算過程を省略してすっきりさせましたが、書かないよりも書いた方が無難です。必要なことを省略してしまえば、減点されてしまうからです。
どうしても判断がつかないときがあるかもしれません。そんなときには、多少長くなったとしても記述しておきましょう。
また、慣れていれば別ですが、考えながら書くのはできるだけ避けましょう。一般に、上手く書けないだけでなく、時間も余計に掛かると言われています。
言われてみればその通りかもしれません。余白を上手に利用して試し書きするのも良いでしょう。答案を作成するのは、少なくとも記述の方針を固めてからにしましょう。
Recommended books
微分・積分を基本から学習できる教材です。まずは参考書3冊。
オススメその1-『崖っぷちシリーズ 数学3の微分積分の検定外教科書 改訂第三版』
ボリューム満点なので、辞書的に利用すると良い教材です。
考え方や解き方を載せている教材は多いですが、どういう解法を選択すれば良いかという視点も解説されています。受験生にとってはありがたい教材です。
オススメその2-『マンガでわかる微分積分 微積ってなにをしているの?どうして教科書はわかりにくいの?』
文字ばかりの参考書が苦手な人向け。マンガと言うよりも挿絵に近い感じですが、イメージを掴むには良いでしょう。
オススメその3-『使い道がわかる微分積分 物理屋が贈る数学講義』
物理でも微積を利用しますが、物理屋さんが微分・積分を丁寧に解説してくれています。数式や計算の前に、基本的な概念から学習できます。
次は問題集を紹介。どれも有名な教材なので、自分に合った1冊を仕上げましょう。
オススメその4-『数学3 基礎問題精講』
コンパクトに収まっているので手回しの良い教材です。ただし、基礎と言っても入試基礎なので注意しましょう。
オススメその5-『1対1対応の演習/数学3(微積分編)新訂版』
こちらも『数学3 基礎問題精講』と同レベル帯の問題集です。解説の分かりやすさで選ぶと良いでしょう。
オススメその6-『微積分/基礎の極意』
難関大なら上の2冊よりもこちらか『数学3 標準問題精講』の方が良いかもしれません。