数学の公式・定理集｜図形と計量

04/30/2021公式・定理,数学１

1. 図形と計量
2. おすすめの数学辞典

図形と計量

三角比の定義とその相互関係

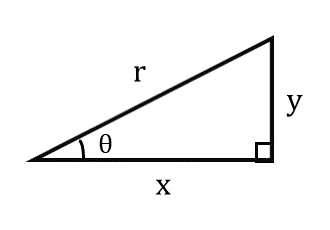
三角比の定義

∠θに対する正弦

$\begin{equation*} \quad \sin \theta = \frac{y}{r} \end{equation*}$

∠θに対する余弦

$\begin{equation*} \quad \cos \theta = \frac{x}{r} \end{equation*}$

∠θに対する正接

$\begin{equation*} \quad \tan \theta = \frac{y}{x} \end{equation*}$

三角比の相互関係

$\begin{align*} & \sin^{2} \theta + \cos^{2} \theta = 1 \\[ 7pt ] & \tan \theta = \frac{\sin \theta}{\cos \theta} \\[ 7pt ] & 1 + \tan^{2} \theta = \frac{1}{\cos^{2} \theta} \end{align*}$

図形と計量｜三角比の相互関係についてその１

$180^{\circ}-\theta \ , \ 90^{\circ} \pm \theta$ の三角比

$\begin{align*} & \sin \left( 180^{\circ}-\theta \right) = \sin \theta \\[ 7pt ] & \cos \left( 180^{\circ}-\theta \right) = -\cos \theta \\[ 7pt ] & \tan \left( 180^{\circ}-\theta \right) = -\tan \theta \end{align*}$

$\begin{align*} & \sin \left( 90^{\circ} \pm \theta \right) = \cos \theta \\[ 7pt ] & \cos \left( 90^{\circ} \pm \theta \right) = \mp \sin \theta \\[ 7pt ] & \tan \left( 90^{\circ} \pm \theta \right) = \mp \frac{1}{\tan \theta} \end{align*}$

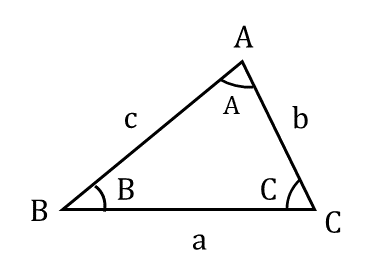
正弦定理

△ABCの外接円の半径をRとすると

$\begin{equation*} \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R \end{equation*}$

余弦定理

$\begin{align*} a^{2} = b^{2} + c^{2} -2bc \cos A \\[ 7pt ] b^{2} = c^{2} + a^{2} -2ca \cos B \\[ 7pt ] c^{2} = a^{2} + b^{2} -2ab \cos C \end{align*}$

参考

$\begin{align*} a = c \cos B + b \cos C \\[ 7pt ] b = a \cos C + c \cos A \\[ 7pt ] c = b \cos A + a \cos B \end{align*}$

三角形の辺と角の関係

三角形の成立条件

$\begin{equation*} |b-c| \lt a \lt b+c \end{equation*}$

辺と角の大小関係その１

$\begin{align*} a \lt b \ & \Longleftrightarrow \ A \lt B \\[ 7pt ] a = b \ & \Longleftrightarrow \ A = B \\[ 7pt ] a \gt b \ & \Longleftrightarrow \ A \gt B \end{align*}$

辺と角の大小関係その２

$\begin{align*} a \lt 90^{\circ} \ & \Longleftrightarrow \ a^{2} \lt b^{2} + c^{2} \\[ 7pt ] a = 90^{\circ} \ & \Longleftrightarrow \ a^{2} = b^{2} + c^{2} \\[ 7pt ] a \gt 90^{\circ} \ & \Longleftrightarrow \ a^{2} \gt b^{2} + c^{2} \end{align*}$