図形と計量｜三角形の面積について

12/18/2021数学１

今回は、三角形の面積について学習しましょう。今さら三角形の面積と思うでしょうが、三角比を使って求めます。

正弦定理や余弦定理を扱うようになると、図形との関わりがより強くなってきたのが分かると思います。三角形の面積もその１つです。

記事の画像が見辛いときはクリックすると拡大できます。

三角形の面積を三角比を使って表す

三角形の面積は、底辺や高さを用いて表されます。

三角形の面積を求めるとき、この公式を使えば良いことはみんな知っています。高校では、この公式を三角比を使って表します。

新しい式が出てきたと言っても、三角比に置き換わっただけです。どの部分が置き換わったのかを知っておきましょう。

三角比を使った式を導出してみよう

公式から分かるように、底辺と高さが分かれば、三角形の面積を求めることができます。ここで三角比を思い出してみましょう。

∠Ａに対する三角比

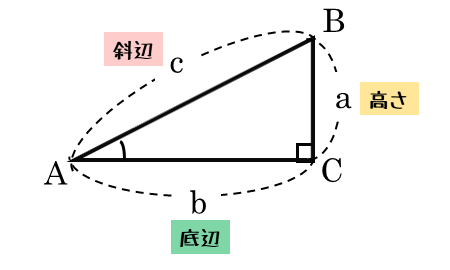
$\triangle ABC$ は直角三角形において

$$\begin{align*} &\quad BC=a \\[ 7pt ] &\quad AC=b \\[ 7pt ] &\quad AB=c \end{align*}$$

とすると

$$\begin{align*} &\quad \sin A = \frac{a}{c} \\[ 7pt ] &\quad \cos A = \frac{b}{c} \\[ 7pt ] &\quad \tan A = \frac{a}{b} \end{align*}$$

この三角比のうち、正弦に注目します。

直角三角形の高さを三角比で表す

$\triangle ABC$ は直角三角形において

$$\begin{align*} \quad \sin A = \frac{a}{c} \end{align*}$$

これを $a$ について変形すると

$$\begin{align*} \quad a=c\sin A \end{align*}$$

正弦の式を変形すると、直角三角形の高さを斜辺と三角比（正弦）を用いて表せることが分かります。

つまり、高さを三角比を用いた式に置き換えることによって、新たな三角形の面積の公式を導出することができます。このことがどんな三角形にも成り立つのかを考えてみましょう。

鋭角三角形の面積

鋭角三角形の面積を考えてみましょう。

△ＡＢＣは鋭角三角形です。辺ＡＢを底辺と考えると、高さは線分ＣＨの長さです。

線分ＣＨは、頂点Ｃから辺ＡＢに下ろした垂線です。

このとき、三角比を用いて、高さＣＨを表します。∠Ａに対する正弦を利用します。

直角三角形の高さを三角比で表す

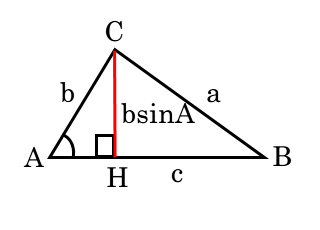
直角三角形である $\triangle ACH$ について、三角比の定義より

$$\begin{align*} \quad \sin A = \frac{CH}{AC} \end{align*}$$

これを $CH$ について変形すると

$$\begin{align*} \quad CH = AC \sin A \end{align*}$$

$AC=b$ より

$$\begin{align*} \quad CH = b \sin A \end{align*}$$

これを三角形の面積の公式に代入して整理すると、三角比を用いた式が得られます。

鋭角三角形の面積

鋭角三角形である $\triangle ABC$ の面積 $S$ は

$$\begin{align*} \quad S &= \frac{1}{2} \cdot AB \cdot CH \\[ 7pt ] &= \frac{1}{2} \cdot c \cdot b \sin A \\[ 7pt ] &= \frac{1}{2} bc \sin A \end{align*}$$

鋭角三角形の面積は、２辺の長さｂ，ｃとその挟む∠Ａに対する正弦ｓｉｎＡで表されることが分かります。

鈍角三角形の面積

鈍角三角形の場合も同じようにして導出します。

△ＡＢＣは鈍角三角形です。辺ＡＢを底辺と考えると、高さは線分ＣＨの長さです。

線分ＣＨは、頂点Ｃから直線ＡＢに下ろした垂線です。ここで、垂線の引き方に注意しましょう。

鈍角三角形の場合、頂点Ｃから辺ＡＢに垂線を下ろせません。このような場合、延長線を引きます。意外とできない人がいるので注意しましょう。

直角三角形ができていますが、角の大きさに注意しましょう。∠ＢＡＣと∠ＣＡＨは、互いに異なる角です。

鈍角三角形の面積

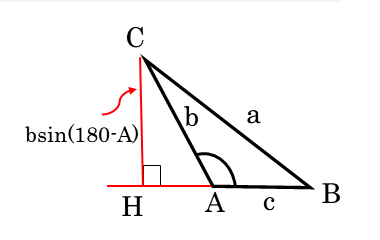
直角三角形である $\triangle BCH$ について、三角比の定義より

$$\begin{align*} \quad \sin {\angle CAH} = \frac{CH}{AC} \end{align*}$$

これを $CH$ について変形すると

$$\begin{align*} \quad CH = AC \sin {\angle CAH} \end{align*}$$

$AC=b \ , \ \angle CAH=180^{\circ}-A$ より

$$\begin{align*} \quad CH = b \sin {\left(180^{\circ}-A \right)} \end{align*}$$

$\sin {\left(180^{\circ}-A \right)}=\sin A$ より

$$\begin{align*} \quad CH = b \sin A \end{align*}$$

∠Ａに対する正弦を用いたわけではありませんが、三角比の拡張を利用するとｓｉｎＡが出てきました。あくまでも結果的にです。どの角に対する正弦なのかを間違えないようにしましょう。

これを三角形の面積の公式に代入して整理すると、三角比を用いた式が得られます。

鈍角三角形の面積

鈍角三角形である $\triangle ABC$ の面積 $S$ は

$$\begin{align*} \quad S &= \frac{1}{2} \cdot AB \cdot CH \\[ 7pt ] &= \frac{1}{2} \cdot c \cdot b \sin A \\[ 7pt ] &= \frac{1}{2} bc \sin A \end{align*}$$

鈍角三角形の場合でも、鋭角三角形と同じ式が導出されました。このように三角形の面積は、２辺の長さとその挟む角に対する正弦とを用いて表されます。

三角比を用いて三角形の面積を求めるときの条件

三角形の面積を求めるとき、三角比を利用できることが分かりました。ただし、このとき、２つの情報が必要になります。

公式を利用するには、条件を満たす必要があります。そのために、角の大きさや辺の長さを先に求めるときもあります。

これが公式や定理をただ暗記しただけでは解けるようにならない理由です。公式や定理に用いられる数量が何かを知らなければ、公式を利用することができません。

次に、三角形の面積を実際に求めてみましょう。