数学の公式・定理集|数と式

数と式
整式の加法・減法・乗法
計算法則:A,B,Cを整数とする。
交換法則
\begin{align*}
&A+B = B+A \\[ 10pt ]
&AB = BA
\end{align*}
結合法則
\begin{align*}
&\left( A+B \right) + C = A+ \left(B+C \right) \\[ 10pt ]
&\left( AB \right) C = A \left( BC \right)
\end{align*}
分配法則
\begin{align*}
&A \left( B+C \right) = AB + AC \\[ 10pt ]
&\left( A+B \right) C = AC + BC
\end{align*}
指数法則:m,nを正の整数とする。
\begin{align*}
a^{m} a^{n} &= a^{m+n} \\[ 10pt ]
{\left( a^{\scriptsize{m}} \right)}^{\scriptsize{n}} &= a^{\scriptsize{mn}} \\[ 10pt ]
{\left( ab \right)}^{\scriptsize{n}} &= a^{\scriptsize{n}} b^{\scriptsize{n}}
\end{align*}
参考
\begin{equation*}
a^{\scriptsize{0}}=1
\end{equation*}
展開の公式、因数分解
\begin{align*}
&\bullet \ {\left( a+b \right)}^{\scriptsize{2}} = a^{\scriptsize{2}} +2ab + b^{\scriptsize{2}} \\[ 10pt ]
&\bullet \ {\left( a-b \right)}^{\scriptsize{2}} = a^{\scriptsize{2}} -2ab + b^{\scriptsize{2}} \\[ 10pt ]
&\bullet \ {\left( a+b \right)}{\left( a-b \right)} = a^{\scriptsize{2}} – b^{\scriptsize{2}} \\[ 15pt ]
&\bullet \ {\left( x+a \right)}{\left( x+b \right)} \\[ 15pt ]
&\quad = x^{2} +\left( a+b \right)x + ab \\[ 15pt ]
&\bullet \ {\left( ax+b \right)}{\left( cx+d \right)} \\[ 10pt ]
&\quad = ac{x}^{\scriptsize{2}} +\left( ad + bc \right)x +bd
\end{align*}
参考
\begin{align*}
&\bullet \ {\left( a+b \right)}{\left( a^{\scriptsize{2}}-ab+b^{\scriptsize{2}} \right)} = a^{\scriptsize{3}} + b^{\scriptsize{3}} \\[ 10pt ]
&\bullet \ {\left( a-b \right)}{\left( a^{\scriptsize{2}}+ab+b^{\scriptsize{2}} \right)} = a^{\scriptsize{3}} – b^{\scriptsize{3}} \\[ 15pt ]
&\bullet \ {\left( a+b \right)}^{\scriptsize{3}} \\[ 10pt ]
&\quad = a^{\scriptsize{3}} + 3{a}^{\scriptsize{2}}b + 3a{b}^{\scriptsize{2}} + b^{\scriptsize{3}} \\[ 15pt ]
&\bullet \ {\left( a-b \right)}^{\scriptsize{3}} \\[ 10pt ]
&\quad = a^{\scriptsize{3}} – 3{a}^{\scriptsize{2}}b + 3a{b}^{\scriptsize{2}} – b^{\scriptsize{3}} \\[ 15pt ]
&\bullet \ a^{\scriptsize{3}} +b^{\scriptsize{3}} +c^{\scriptsize{3}} -3abc \\[ 10pt ]
&= {\left( a+b+c \right)}{\left( a^{\scriptsize{2}} +b^{\scriptsize{2}} +c^{\scriptsize{2}} -ab -bc-ca \right)}
\end{align*}
関連記事
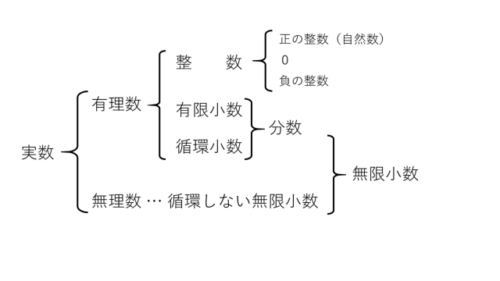
実数、平方根
実数の構造
関連記事
絶対値の性質
\begin{align*}
&a \geqq 0 \ \text{のとき} \quad |a|=a \\[ 10pt ]
&a \lt 0 \ \text{のとき} \quad |a|=-a
\end{align*}
\begin{equation*}
{|a|}^{\scriptsize{2}}=a^{\scriptsize{2}}
\end{equation*}
平方根の性質
\begin{align*}
&a \geqq 0 \ \text{のとき} \\[ 10pt ]
&\quad {\left( \sqrt{a} \right)}^{\scriptsize{2}}=a \\[ 10pt ]
&\quad {\left( -\sqrt{a} \right)}^{\scriptsize{2}}=a \\[ 10pt ]
&\quad \sqrt{a} \geqq 0
\end{align*}
\begin{align*}
&a \geqq 0 \ \text{のとき} \quad \sqrt{a^{\scriptsize{2}}} = a \\[ 10pt ]
&a \lt 0 \ \text{のとき} \quad \sqrt{a^{\scriptsize{2}}} = -a \\[ 10pt ]
&\text{すなわち} \quad \sqrt{a^{\scriptsize{2}}} = |a|
\end{align*}
\begin{align*}
&a \gt 0 \ , \ b \gt 0 \ , \ k \gt 0 \ \text{のとき} \\[ 10pt ]
&\quad \sqrt{a} \sqrt{b} = \sqrt{ab} \\[ 10pt ]
&\quad \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \\[ 10pt ]
&\quad \sqrt{k^{\scriptsize{2}} a} = k \sqrt{a}
\end{align*}
関連記事
2重根号のはずし方
文字はすべて正の数とする。
1. 根号の中の式を変形する
\begin{align*}
\quad \sqrt{p \pm k\sqrt{q}} = \sqrt{\left( a+b \right) \pm 2\sqrt{ab}}
\end{align*}
2. 根号の中の式を因数分解して2重根号を外す。
\begin{align*}
\quad \sqrt{\left( a+b \right) \pm 2\sqrt{ab}}=\sqrt{a} \pm \sqrt{b}
\end{align*}
ただし、a>b
関連記事
1次不等式
不等式の性質
\begin{align*}
&a \lt b \ \text{ならば} \\[ 10pt ]
&\quad a+c \lt b+c \\[ 10pt ]
&\quad a-c \lt b-c
\end{align*}
\begin{align*}
&a \lt b \ , \ 0 \lt c \ \text{ならば} \\[ 10pt ]
&\quad ac \lt bc \\[ 10pt ]
&\quad \frac{a}{c} \lt \frac{b}{c}
\end{align*}
\end{align*}
\begin{align*}
&a \lt b \ , \ c \lt 0 \ \text{ならば} \\[ 10pt ]
&\quad ac \gt bc \\[ 10pt ]
&\quad \frac{a}{c} \gt \frac{b}{c}
\end{align*}
\begin{align*}
&a \lt b \ , \ b \lt c \ \text{ならば} \\[ 10pt ]
&\quad a \lt c
\end{align*}
絶対値を含む方程式や不等式
場合分け
\begin{equation*}
\left| A \right| =
\begin{cases}
A & \left( A \geqq 0 \right) \\[ 10pt ]
-A & \left( A \lt 0 \right)
\end{cases}
\end{equation*}
簡便法
\begin{align*}
& c \gt 0 \ \text{のとき} \\[ 15pt ]
& \bullet \ \text{方程式} \ |x| = c \ \text{の解} \\[ 10pt ]
& \quad x = \pm c \\[ 15pt ]
& \bullet \ \text{不等式} \ |x| \lt c \ \text{の解} \\[ 10pt ]
& \quad -c \lt x \lt c \\[ 15pt ]
& \bullet \ \text{不等式} \ |x| \gt c \ \text{の解} \\[ 10pt ]
& \quad x \lt -c \ , \ c \lt x
\end{align*}
集合
Uは全体集合で、A,B,CはUの部分集合とする。
集合の基本
部分集合
\begin{align*}
&\text{$A \subset B$ であるとき} \\[ 10pt ]
&\quad \text{「$x \in A$ ならば $x \in B$」} \\[ 10pt ]
&\text{が成り立つ。} \\[ 10pt ]
&\text{集合 $A$ は集合 $B$ の部分集合}
\end{align*}
相等
\begin{align*}
&\text{$A = B$ であるとき} \\[ 10pt ]
&\quad \text{「$A \subset B$ かつ $A \supset B$」} \\[ 10pt ]
&\text{が成り立つ。} \\[ 10pt ]
&\text{集合 $A$ と集合 $B$ は等しい}
\end{align*}
共通部分
\begin{equation*}
\text{$A \cap B =\{ x \ | \ x \in A \ \text{かつ} \ x \in B \}$}
\end{equation*}
和集合
\begin{equation*}
\text{$A \cup B =\{ x \ | \ x \in A \ \text{または} \ x \in B \}$}
\end{equation*}
補集合
\begin{equation*}
\text{$\overline{ A } =\{ x \ | \ x \in U \ \text{かつ} \ x \notin A \}$}
\end{equation*}
関連記事
ド・モルガンの法則
\begin{align*}
\overline{ A \cup B } &= \overline{ A } \cap \overline{ B } \\[ 10pt ]
\overline{ A \cap B } &= \overline{ A } \cup \overline{ B }
\end{align*}
\begin{align*}
\overline{ A \cup B \cup C } &= \overline{ A } \cap \overline{ B } \cap \overline{ C } \\[ 10pt ]
\overline{ A \cap B \cap C } &= \overline{ A } \cup \overline{ B } \cup \overline{ C }
\end{align*}
命題と条件
命題の真偽
真の場合:証明する
偽の場合:反例を1つ挙げる
関連記事
必要・十分条件
\begin{align*}
&\text{2つの条件 $p \ , \ q$ について} \\[ 10pt ]
\bullet \ &\text{$p \Rightarrow q$ が真であるとき} \\[ 10pt ]
&\text{$q$ は $p$ であるための必要条件} \\[ 10pt ]
&\text{$p$ は $q$ であるための十分条件} \\[ 15pt ]
\bullet \ &\text{$p \Rightarrow q \ , \ q \Rightarrow p$ がともに真であるとき} \\[ 10pt ]
&\text{$q$ は $p$ ( $p$ は $q$ )であるための必要十分条件}
\end{align*}
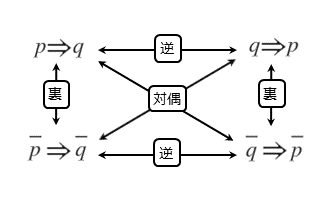
命題の逆、対偶、裏
おすすめの数学辞典
公式や定理をまとめた数学辞典です。1冊あると便利です。
おすすめ その1
導出が丁寧に記載されている公式集を1冊もっておくと困ったときに辞書代わりになります。 ポケットサイズのものと違いサイズが少し大きいので、図が豊富です。
おすすめ その2
公式・定理・定義は左ページ、活用例・解説・証明は右ページの見開き構成になっているので、使いやすいです。
おすすめ その3
難関大を志望している人向けです。大学に進学してからも使えます。