集合と論理|命題について

今回は命題について学習しましょう。
新しい用語や定義を理解するには、すでに学習した集合や要素の知識が必要になります。既習内容と新規内容とをスムーズに接続するためにも、不安のある人は復習しておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
命題と条件、否定について
この単元では、命題・条件・否定という用語が出てきます。それぞれの定義をしっかり覚えましょう。
用語の定義に合わせて、記号の使い方や表し方もしっかりマスターしましょう。
命題について
命題とは、正しいか正しくないかを判定できる文や式のことです。正しいか正しくないかを判定できないものは命題とは言いません。
命題の一例
具体例1:「3は偶数である」
3は奇数であって偶数ではないので、正しくないと判定できる。よって、「3は偶数である」は命題と言える。
具体例2:「1+1」
正しいか正しくないかを判定できない。よって、「1+1」は命題と言えない。
このように、正しいか正しくないかを判定できるものを命題と言います。
判定するためには、「~である」のような結論があることもポイント。
命題の真偽
命題が正しいことを「命題は真である」と言い、命題が正しくないことを「命題は偽である」と言います。
具体例1で挙げた「3は偶数である」という命題は、正しくありませんでした。ですから、命題「3は偶数である」は偽である、と言います。
正しい=真、正しくない=偽
条件について
命題の中でも少し特殊な命題があります。それはxやaなどの変数を用いた文や式です。このように変数を用いた命題のことを条件と言います。
条件の一例
具体例1:「x>0」
具体例2:「xは整数」
条件と言われる命題が特殊なのは、変数の値が決まると命題の真偽を判定できるところです。言い換えると、変数の値が決まらないと真偽を判定できません。
命題が文字を含む文や式になっていたら条件。
2つの条件からなる命題
「3は偶数である」のように、命題は必ず1つの文や式からできているとは限りません。先ほど紹介した条件を2つ組み合わせた命題もあります。
条件を2つ用いた命題の一例
「xが奇数であるならば、5xは奇数である」
「xが奇数である」と「5xは奇数である」は変数を用いた命題なので、ともに条件。
このように、1つの命題が、条件と言われる命題を2つ含むこともあります。
このような命題を一般に「pならばq」と言い、記号を使って「p⇒q」と表します。また、条件pを仮定、条件qを結論と言います。
命題「pならばq(p⇒q)」の真偽を考える問題は頻出。「条件pならば、条件q」=「仮定ならば、結論」
2つの条件からなる命題の真偽
命題「pならばq(p⇒q)」の真偽は、「仮定pが真となる変数が、結論qでも真となる変数であるか」を考えることで真偽を判定することができます。
条件pが真だと仮定として、条件qの結論が真であるかを判定すれば良いので、条件pを満たす変数が、条件qを満たす変数であるかを調べます。
条件pを満たす変数xの値だけで、結論である条件qを満たすかどうかを判定しよう。
真偽を判定してみよう
具体例として、命題「xが奇数であるならば、5xは奇数である」の真偽を考えてみましょう。
仮定と結論は以下の通りです。
仮定:xが奇数である
結論:5xは奇数である
仮定「xが奇数である」が真となる変数xを考えます。
仮定を満たす変数xの値を考える 1⃣
仮定「$x$ が奇数である」が真となる変数 $x$ の値は
\begin{align*} \quad x=1 \ , \ 3 \ , \ 5 \ , \ 7 \ , \ \cdots \end{align*}これらが結論「5xは奇数である」でも真となる変数であるかを調べます。
仮定を満たす変数xの値を考える 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] \quad x &=1 \ , \ 3 \ , \ 5 \ , \ 7 \ , \ \cdots \end{align*}これらが結論「$5x$ は奇数である」を満たすか調べると
\begin{align*} \quad 5x &=5 \cdot 1 \ , \ 5 \cdot 3 \ , \ 5 \cdot 5 \ , \ 5 \cdot 7 \ , \ \cdots \\[ 7pt ] &=5 \ , \ 15 \ , \ 25 \ , \ 35 \ , \ \cdots \end{align*}より、結論を満たすので、結論も真となる。
よって、命題は真。
仮定が真となる変数の値は、結論も真となる変数の値になるので、命題「xが奇数であるならば、5xは奇数である」は真であると言えます。
なお、命題が偽であるときには、偽となる変数の値を一例として挙げるのが一般的です。この挙げた一例のことを反例と言います。
命題の真偽を集合や要素を利用して判定する
次は、命題と集合や要素との関係を考えてみましょう。
条件が真となる変数を集合や要素に置き換える
命題「pならばq(p⇒q)」の真偽を調べるとき、条件p,qが真となる変数の値を考えます。
このとき、変数の値は複数ある場合がほとんどなので、集合や要素に置き換えると、命題の真偽を判定しやすくなります。
条件pが真となる変数の値を要素として、その集まりを集合Pとします。同じようにして、条件qが真となる変数の値を要素として、その集まりを集合Qとします。
集合や要素への置き換え
- 条件が真となる変数の値=要素
- 変数の値の集まり=要素の集まり、すなわち集合
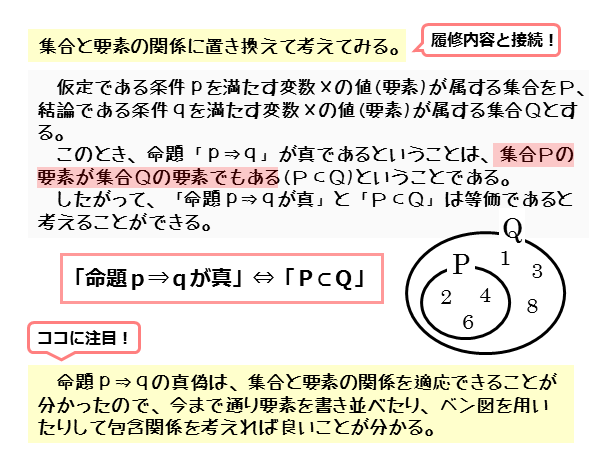
命題「pならばq(p⇒q)」が真であるとき、集合Pの要素は、集合Qの要素でもあります。つまり、集合Pは集合Qの部分集合となるので、「P⊂Q」が成り立ちます。
このことから、「命題pならばq(p⇒q)が真である」と「集合P,Qについて、P⊂Q」は等価(同値)であることが分かります。
今後、命題「pならばq(p⇒q)」の真偽の判定では、集合や要素を利用しましょう。特に、ベン図を使うと、包含関係を可視化できます。
また、条件p,qが不等式で与えられていれば、ベン図よりも数直線の方が有効です。
仮定や結論が真となる変数の値は複数あるので、集合や要素に置き換えて考えよう。その際、ベン図を上手に使おう。
条件の否定
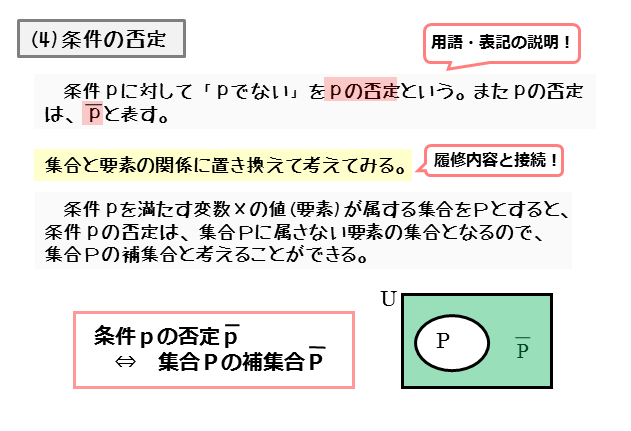
条件pに対して、条件pでないものを条件pの否定と言います。条件pの否定は、pの上に横線を引いて $\overline{p}$ と表します。
この条件の否定も集合と要素に置き換えることができます。否定の表し方が補集合と同じ表し方だと気付いた人は、良く復習していると思います。
条件pを満たす変数の値(=要素)の集合を集合Pとします。条件pの否定が真となる変数の値は、条件pが真となる変数の値以外です。
これを集合で言えば、集合Pに属さない要素の集合となります。つまり、条件pの否定が真となる変数の値を要素とする集合は、集合Pの補集合になります。
このことから「条件pの否定」と「集合Pの補集合」は等価(同値)であることが分かります。
条件の否定でもベン図を積極的に使おう。
ド・モルガンの法則を利用した命題の書き換え
条件の否定を扱った命題では、その真偽を判定するのが面倒な場合があります。そこで、条件の否定ならば、補集合を利用できることを利用します。
補集合を扱えるということは、「ド・モルガンの法則」も利用できるということです。
ド・モルガンの法則
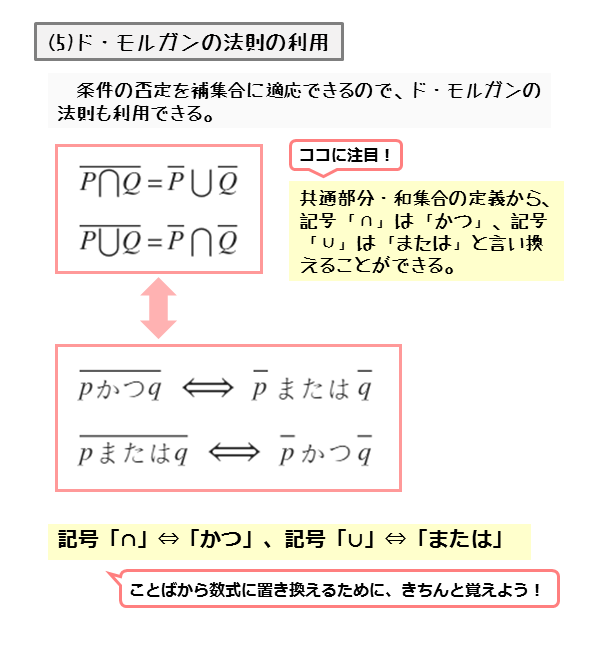
\begin{align*} \quad \overline{P \cap Q} &= \overline{P} \cup \overline{Q} \\[ 7pt ] \overline{P \cup Q} &= \overline{P} \cap \overline{Q} \end{align*}ド・モルガンの法則を利用すれば、命題そのものを書き換え可能になるので、命題の真偽を判定しやすくなります。命題の書き換えは、ド・モルガンの法則をそのまま利用します。
ド・モルガンの法則を利用した命題の書き換え
\begin{align*} \quad \overline{p \ \scriptsize{\text{かつ}} \ q} \ &= \ \overline{p} \ \scriptsize{\text{または}} \ \overline{q} \\[ 7pt ] \overline{p \ \scriptsize{\text{または}} \ q} \ &= \ \overline{p} \ \scriptsize{\text{かつ}} \ \overline{q} \end{align*}注意したいのは、記号とことばの対応関係です。共通部分の記号「⋂」は「かつ」に対応し、和集合の記号「⋃」は「または」に対応します。
数学はことばを数式に置き換える(=翻訳する)科目なので、日頃からことばと数式の対応関係に注意しよう。
次は命題を扱った問題を実際に解いてみましょう。