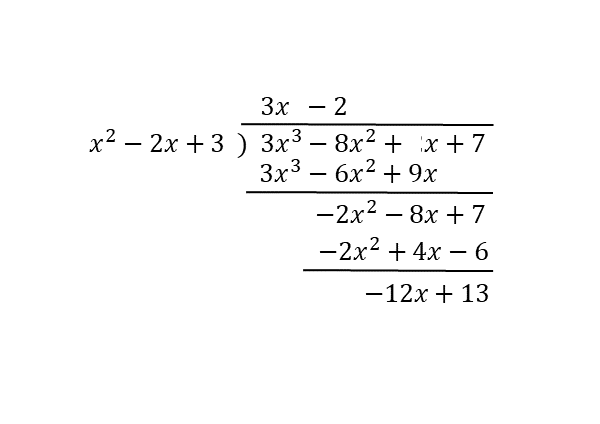複素数と方程式｜高次式の値について

05/24/2021数学２

高次式の値を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

$\begin{align*} &\text{$x=1-\sqrt{2}i$ のとき} \\[ 5pt ] &\quad 3x^{\scriptsize{3}}-8x^{\scriptsize{2}}+x+7 \\[ 7pt ] &\text{の値を求めよ。} \end{align*}$

問の解答・解説

例題(3)が単独で出題された形式です。入試ではこの形式での出題が多く、ほとんどの人は最初から代入して計算するかもしれません。

ここでは、次数を下げるという考えを意識して解きます。与えられた複素数を解にもつ２次方程式を導きます。

問の解答例 1⃣

$\begin{align*} &\quad P=3x^{\scriptsize{3}}-8x^{\scriptsize{2}}+x+7 \\[ 7pt ] &\text{とおく。} \\[ 5pt ] &\text{$x=1-\sqrt{2}i$ より} \\[ 5pt ] &\quad x-1=-\sqrt{2}i \\[ 7pt ] &\text{両辺を $2$ 乗すると} \\[ 5pt ] &\quad \left(x-1 \right)^{\scriptsize{2}}=-2 \\[ 7pt ] &\text{これを整理すると} \\[ 5pt ] &\quad x^{\scriptsize{2}}-2x+3=0 \quad \cdots \text{①} \end{align*}$

①式は、与えられた複素数を解にもつ２次方程式です。どうしても信じられないのであれば、与えられた複素数を代入してみると良いでしょう。等式が成り立つはずです。

①式を割る式として、与式を割り算します。筆算すると以下のようになります。

商と余りが１次式で得られました。余りの次数は、割る式の次数よりも小さくなっています。

筆算の結果と割り算の基本公式を利用して、与式の次数を下げます。

問の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x^{\scriptsize{2}}-2x+3=0 \quad \cdots \text{①} \\[ 7pt ] &\text{与式 $P$ を $x^{\scriptsize{2}}-2x+3$ で割った結果から} \\[ 5pt ] &\quad P=\left(x^{\scriptsize{2}}-2x+3 \right) \left(3x-2 \right)-12x+13 \end{align*}$

３次式である与式を、２次式と１次式で表すことができました。

①式を用いると、余りだけが残ります。このとき、与えられた複素数も代入しましょう。

問の解答例 3⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad P=\left(x^{\scriptsize{2}}-2x+3 \right) \left(3x-2 \right)-12x+13 \\[ 7pt ] &\text{①と $x=1-\sqrt{2}i$ より} \\[ 5pt ] &\quad P=0-12\left(1-\sqrt{2}i \right)+13 \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad P=1+12\sqrt{2}i \end{align*}$

①式から分かるように、与えられたｘの値を代入すると、割る式の値は０になります。商がどのような値になっても割る式は０なので、これらの積を計算する必要はありません。０と記述しましょう。

このような手順を踏めば、実質的に１次式の値を求める問題にまで置き換えることができます。ここまで次数を下げることができれば、ミスなく計算できるでしょう。

問の別解例

次数を下げるという考え方で解く場合、以下のような解法もあります。

問の別解例

$\begin{align*} &\text{$x=1-\sqrt{2}i$ より} \\[ 5pt ] &\quad x-1=-\sqrt{2}i \\[ 7pt ] &\text{両辺を $2$ 乗すると} \\[ 5pt ] &\quad \left(x-1 \right)^{\scriptsize{2}}=-2 \\[ 7pt ] &\text{これを整理すると} \\[ 5pt ] &\quad x^{\scriptsize{2}}-2x+3=0 \quad \cdots \text{①} \\[ 7pt ] &\text{①より} \\[ 5pt ] &\quad x^{\scriptsize{2}}=2x-3 \\[ 7pt ] &\text{よって} \\[ 5pt ] &\qquad 3x^{\scriptsize{3}}-8x^{\scriptsize{2}}+x+7 \\[ 7pt ] &\quad =3x\left(2x-3 \right)-8\left(2x-3 \right)+x+7 \\[ 7pt ] &\quad =6x^{\scriptsize{2}}-24x+31 \\[ 7pt ] &\quad =6\left(2x-3 \right)-24x+31 \\[ 7pt ] &\quad =-12x+13 \\[ 7pt ] &\quad =-12\left(1-\sqrt{2}i \right)+13 \\[ 7pt ] &\quad =1+12\sqrt{2}i \end{align*}$

２次方程式も等式の一種なので、左辺と右辺が等しいという性質があります。ですから左辺を右辺に、または右辺を左辺に置き換えることができます。

与えられた複素数を解にもつ２次方程式（①式）を変形し、それを与式の２次の項に代入しています。１次式を代入するので、次数が下がります。この解法でも、与式の次数が１次まで下がります。

先に述べた解答例では、２次方程式の左辺を丸ごと利用します。それに対して、別解例では、２次方程式を与式に合わせて変形したものを利用します。

どちらも次数を下げるという考え方は共通していますが、①式の利用の仕方が異なります。どちらの視点も大切なので、視野を広げるためにもマスターしておきましょう。

別解例で行われている次数の下げ方は、３乗根を扱った問題でよく利用されます。

Recommended books

紹介するのは、高校数学の授業についていけずに焦っている人向けの教材です。授業についていけない原因は色々と考えられますが、その中でも中学で学習した内容を理解していないことが大半を占めているかもしれません。

高校１年生の場合、数学の内容はほとんどが中学の応用みたいなものです。ですから、予習が進まない、授業についていけない、などがあれば、中学の学習内容を確認することをお勧めします。確認すれば分かりますが、意外と理解していなかったことに気付くはずです。

高校２，３年生にとっては、今さら中学の復習なんかやってられないと思うかもしれません。しかし、理解できない箇所が出てくれば、嫌でも前の単元に戻らなければなりません。そうやって単元をさかのぼっていくと、結局、中学内容に行き着くことも少なくありません。

特に、苦手科目については効果的だと思います。高校での学習に行き詰っている人は、変なこだわりを捨てて、中学内容まで戻ってみると良いでしょう。案外、もっと早く取り組んでいれば良かったと思うかもしれません。

オススメ－『高校入試「解き方」が身につく問題集』シリーズ

学習内容の理解の深度を知るには、問題を解くことが一番分かりやすいです。レベル別に問題を解けば、理解度をより詳細に知ることができるでしょう。このことは、中学内容だろうと高校内容だろうと変わりません。

『高校入試「解き方」が身につく問題集』シリーズは、高校入試対策用の問題集になりますが、頻出の問題を扱っているので、重要事項やその使い方を効率良く確認することができます。

高校入試「解き方」が身につく問題集シリーズ

入試レベルなので応用的な問題が多いですが、高校の授業についていくにはそのくらいの理解度が必要です。つまり、高校数学についていけないとすれば、中学数学の応用レベルに達していない箇所が足枷になっている可能性が高いです。

目安としては、高校入試レベルの問題が８割以上解けることを目標にすると良いでしょう。８割取れるようになれば、高校の学習において、多少の躓きはあっても遅れを取ることは少ないでしょう。

「暗記では解けない問題の解き方」を身につける！
★「出題頻度が高い」＆「解き方にコツがある」問題をマスターして得点アップ！
公立高校入試の問題は、難度の幅が広く、暗記で解ける問題と解き方（考え方）が必要な問題があります。一部の問題は演習量よりも、解き方を押さえてから演習したほうが効率的に点数を上げることができます。本書で選んだ問題をマスターすることで、入試の得点アップにつながります。
★徹底的に「解き方」に焦点を当てた解説！
「例題」「解き方チェック問題」「実践問題の解答解説」のすべてで「解き方」のチェックポイントに沿った解説をしています。