式と証明｜整式の割り算について
今回は、整式の割り算について学習しましょう。
整式の割り算は、基本的に筆算で行います。基本的な流れは数での筆算と同じ要領でできます。
ただし、数のときよりも丁寧に筆算しないと、計算ミスをしやすいので注意が必要です。
整式の割り算について
整数の割り算（除法）については、整数の性質の単元ですでに学習しています。
ここでは、対象が整数ではなく「整式」です。整式になると難しそうな感じがしますが、身構えるほどの難しさではありません。
単項式の割り算であれば暗算することも可能ですが、多項式である整式の場合、暗算するのは難しいです。ですから、筆算で割り算します。
これまでの割り算と比べると、計算は多少面倒になりますが、基本的な流れはそれほど変わりません。ポイントを押さえてコツを掴みましょう。
割り算の基本公式
整数の性質で学習したことの復習になりますが、もう一度確認しておきましょう。整数ａと自然数ｂについて、一般に以下のようなことが成り立ちます。
整数の表し方
このような関係が成り立つとき、ｑのことをａをｂで割った商、ｒのことをａをｂで割った余りと言います。
これと同じようなことが整式の割り算についても成り立ちます。
割り算の基本公式
同じ $1$ つの文字についての $2$ つの整式 $A \ , \ B \ (B \neq 0)$ において、$A$ を $B$ で割ったときの商を $Q$、余りを $R$ とすると
\begin{equation*} \quad A = BQ + R \end{equation*}ただし、$R$ は $0$ か、$B$ より次数の低い整式
割られる整式Ａは、割る整式Ｂ、商Ｑ、余りＲの３つを用いて表されます。余りの条件はよく使われるので、きちんと覚えておきましょう。
整式になっても、単項式が多項式になっただけで、整数のときと変わらないことが分かります。
(割られる数や式)＝(割る数や式)×(商)＋(余り)
ただし、余りの条件に気をつけよう。
整式の割り算の注意点
整式Ａを整式Ｂで割るときに注意したいことが２つあります。
整式の割り算での注意事項
- 整式Ａも整式Ｂも降べきの順に整理してから、割り算を行う。
- 余りの次数が、割る整式Ｂの次数より低くなるか、余りが０になるまで計算を続ける。
どちらの注意事項にも言えることは、「次数に注意を払え」ということです。整式には桁というものがありません。その代わり、次数で判断します。
また、数では大小を比較できますが、整式ではいつも大小を比較できるとは限りません。たとえば、ｘとｘ2を考えてみましょう。
整式の大小関係は条件なしでは決まらない!?
比較結果から分かるように、整式では無条件に大小関係が決まるわけではありません。桁の概念もなく、大小も一意に決まらないことから、整式の割り算では、次数に注目します。次数には高低があるからです。
数の割り算では、桁の大きい方から順に計算していきますが、それと同じように、整式の割り算では、次数の高い方から順に計算していきます。桁を次数に置き換えたと考えると分かりやすいかもしれません。
また、降べきの順に整理することで、最高次数の項が、いつも整式の先頭にある状態になります。このおかげで、整式の割り算では、先頭にある項だけに注意を払えば済むようになります。
整式の割り算では、いつも次数に注意を払おう。
整式の割り算に挑戦してみよう
整式の割り算を具体例で見てみましょう。
例題
次の整式 $A$ を整式 $B$ で割った商と余りを求めよ。
\begin{equation*} \quad A=3x^{\scriptsize{3}}+8+7x \ , \ B=x-1 \end{equation*}降べきの順に並んでいるか、次数の欠けがないか
割り算を始める前に、２つの整式をよく観察します。整式Ａの方を見ると、１次の項が一番最後にあります。
与式を文字ｘについて降べきの順に整理します。
与式を降べきの順に整理する
整式 $A$ を $x$ について降べきの順に整理すると
\begin{align*} \quad A &= 3x^{\scriptsize{3}}+8+7x \\[ 7pt ] &= 3x^{\scriptsize{3}} \underline{+7x+8} \end{align*}整式Ａについては降べきの順に並べることが最優先ですが、実はもう１点気付いておきたいことがあります。それは２次の項がないことです。
このように欠けている次数の項があれば、筆算の際に、その項を空けて記述するようにしましょう。
スペースを空けないで計算すると、上下に次数が揃わなくなります。そうすると、引き算するときに苦労し、最悪、計算ミスをします。
わざわざ計算ミスを誘うような記述を自分から進んで行う必要はないと思います。
整式の割り算では、欠けた次数の項が存在するタイプがよく出題されます。計算ミスをしやすいからです。自分なりに計算ミスをしにくい記述を心掛けましょう。
商を決める
筆算の準備ができたら、商を決めて割り算していきます。このとき、最高次数の項に注目して商を決めます。
数の割り算と異なるところと言えば、商の決め方でしょう。
数の割り算では、割られる数より小さく、かつできるだけ近い数、または割られる数と等しい数になるように商を決めます。
しかし、整式では大小関係が一意に決まらないので、そのような決め方をすることはできません。
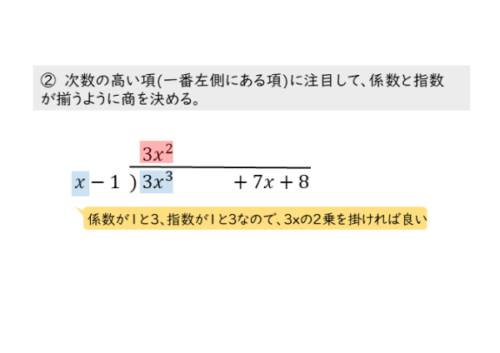
最高次数の項に注目して商を決める
$x$ に何を掛ければ $3x^{\scriptsize{3}}$ となるか：$3x^{\scriptsize{2}}$
よって、商は $3x^{\scriptsize{2}}$
商は、割る整式Ｂの最高次数の項と掛け算したとき、整式Ａの最高次数の項と等しくなるようなものにします。このとき、係数と指数をそれぞれ個別に考えると商を決めやすくなります。
全く同じ項になるように商を考えれば良いので、数の割り算よりもやりやすいかもしれません。
割る整式と商を掛け算、そして引き算
商が決まったら、割る整式Ｂと商を掛け算します。
割る整式Ｂは多項式で、商は単項式です。ですから、分配法則を用いて掛け算します。
掛け算の結果は、割られる整式Ａの下に書きます。この辺りは、数の割り算と同じ要領です。
ただし、引き算しやすいように、次数の同じ項が上下に並ぶように書きましょう。スペースを空けるのもこのためです。
掛け算が終わったら、整式Ａと引き算します。この引き算で、最高次数の項（ここでは３ｘ3）がなくなります。ここまでが整式の割り算の１セットです。
整式の割り算の１セット
- 引き算のとき、最高次数の項が消えるように商を決める。
- 割る整式と商を分配法則で掛け算する。
- 掛け算の結果で引き算する。
この作業を繰り返すことが、整式の割り算です。
引き算の結果を見ると、０にならず、余り（ここでは３ｘ2）が出てきました。
余りは２次式なので、まだ割る整式の次数よりも高いことが分かります。
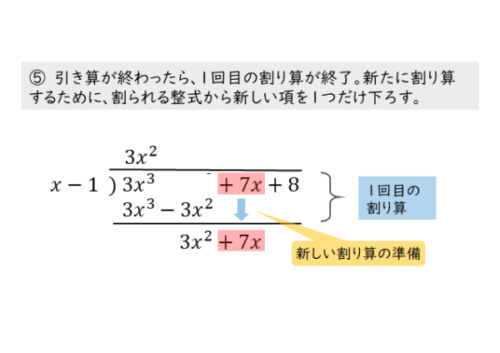
割り算を続けるために、整式Ａの残りの項（ここでは７ｘ）を下に降ろします。
新たな割り算を行います。ここでも、余りの中で最高次数の項（ここでは３ｘ2）に注目して商を決めます。
次数の高い項に注目して商を決める（２セット目）
$x$ に何を掛ければ $3x^{\scriptsize{2}}$ となるか：$3x$
よって、商は $3x$
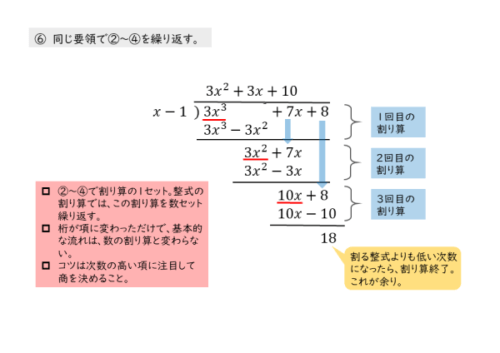
あとは同じ要領で計算していきます。余りが０になれば、割り切れたということで計算を終えます。
また、余りの次数が、割る整式Ｂの次数より低くなれば、商が決まらないので、このときも計算を終えます。
セットを繰り返す回数は、割る整式Ｂの次数によります。
例の場合であれば、整式Ｂが１次式なので、余りが定数（０次）になるまで繰り返す必要があります。
整式の割り算のコツは、割られる整式や余りの最高次数の項をつねに意識することです。商を考えるときも、まだ計算を続けるべきかも最高次数の項を見れば判断することができます。
とにかく、最高次数の項を順に消すことを繰り返すのが、整式の割り算。
次は、整式の割り算を実際に解いてみましょう。