式と証明｜整式の割り算について

07/17/2021数学２

整式の割り算を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

次の整式 $A$ を整式 $B$ で割った商と余りを求めよ。

また、その結果を $A=BQ+R$ の形に書け。

\begin{align*} &(1) \quad A=6x^{\scriptsize{2}}-7x-20 \ , \ B=2x-5 \\[ 7pt ] &(2) \quad A=(2x^{\scriptsize{2}}-3x+1)(x+1) \ , \ B=x^{\scriptsize{2}}+4 \\[ 7pt ] &(3) \quad A=x^{\scriptsize{4}}-2x^{\scriptsize{3}}-x+8 \ , \ B=2-x-2x^{\scriptsize{2}} \end{align*}

整式によっては、計算ミスをしやすい割り算があります。自分なりに工夫しながら、丁寧に計算しましょう。

問(1)の解答・解説

問(1)

次の整式 $A$ を整式 $B$ で割った商と余りを求めよ。

また、その結果を $A=BQ+R$ の形に書け。

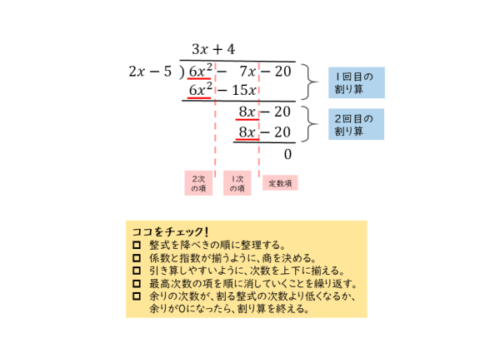
\begin{equation*} \quad A=6x^{\scriptsize{2}}-7x-20 \ , \ B=2x-5 \end{equation*}

どちらの整式も降べきの順に並んでおり、また、欠けている次数の項もありません。最高次数の項に注目しながら商を決め、計算していきます。

割り算の結果は以下の通りです。

筆算によって、整式Ａを整式Ｂで割った商と余りが分かりました。割り算の基本公式で表します。

問(1)の解答例

整式 $A$ を整式 $B$ で割った商と余りは

\begin{align*} &\quad \text{商} \ 3x+4 \\[ 7pt ] &\quad \text{余り} \ 0 \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad 6x^{\scriptsize{2}}-7x-20 = (2x-5)(3x+4) \end{align*}

問(1)は、欠けた次数がなく、降べきの順に整理された整式の割り算でした。基本レベルですが、ポイントを押さえるまではこのレベルの問題をこなすと良いでしょう。

問(2)の解答・解説

問(2)

次の整式 $A$ を整式 $B$ で割った商と余りを求めよ。

また、その結果を $A=BQ+R$ の形に書け。

\begin{equation*} \quad A=(2x^{\scriptsize{2}}-3x+1)(x+1) \ , \ B=x^{\scriptsize{2}}+4 \end{equation*}

問(2)は、一瞬、戸惑う問題かもしれません。整式Ａが因数分解された状態です。このような場合、降べきの順に並んでいないものとして、展開しましょう。

問(2)の解答例 1⃣

整式 $A$ を展開すると

\begin{align*} \quad A &= (2x^{\scriptsize{2}}-3x+1)(x+1) \\[ 7pt ] &= 2x^{\scriptsize{3}} -x^{\scriptsize{2}} -2x+1 \end{align*}

次に、整式Ｂで割り算しますが、整式Ｂには１次の項がありません。欠けていることが分かるように、１次の項を空けて記述します。

問(1)のときよりも注意深く計算しましょう。割り算の結果は以下の通りです。

筆算によって、整式Ａを整式Ｂで割った商と余りが分かりました。割り算の基本公式で表します。

問(2)の解答例 2⃣

整式 $A$ を整式 $B$ で割った商と余りは

\begin{align*} &\quad \text{商} \ 2x-1 \\[ 7pt ] &\quad \text{余り} \ -10x+5 \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad (2x^{\scriptsize{2}}-3x+1)(x+1) = (x^{\scriptsize{2}}+4)(2x-1)-10x+5 \end{align*}

欠けている次数の項があると、意外と計算ミスしやすくなります。スペースをきちんと空けて、その項がないことを意識できるようにしましょう。

問(3)の解答・解説

問(3)

次の整式 $A$ を整式 $B$ で割った商と余りを求めよ。

また、その結果を $A=BQ+R$ の形に書け。

\begin{equation*} \quad A=x^{\scriptsize{4}}-2x^{\scriptsize{3}}-x+8 \ , \ B=2-x-2x^{\scriptsize{2}} \end{equation*}

整式Ｂを見ると、降べきの順に並んでいません。これを並べ替えて整理します。

問(3)の解答例 1⃣

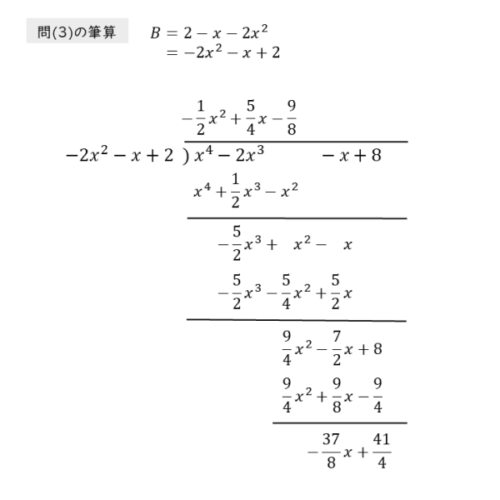
整式 $B$ を降べきの順に整理すると

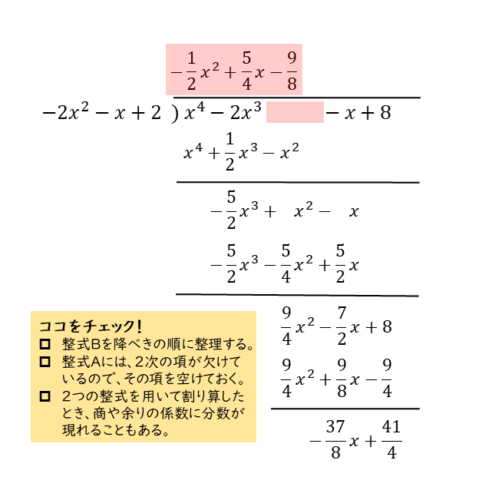
\begin{align*} \quad B &= 2-x-2x^{\scriptsize{2}} \\[ 7pt ] &= -2x^{\scriptsize{2}}-x+2 \end{align*}

次に、割り算を行いますが、整式Ａには２次の項がありません。欠けた項があることが分かるように、２次の項を空けて記述します。

引き算で計算ミスをしやすいので、細心の注意を払って計算しましょう。割り算の結果は以下の通りです。

筆算によって、整式Ａを整式Ｂで割った商と余りが分かりました。割り算の基本公式で表します。

問(3)の解答例 2⃣

整式 $A$ を整式 $B$ で割った商と余りは

\begin{align*} &\quad \text{商} \ -\frac{1}{2} x^{\scriptsize{2}}x+\frac{5}{4} x-\frac{9}{8} \\[ 7pt ] &\quad \text{余り} \ -\frac{37}{8} x+\frac{41}{4} \\[ 7pt ] &\text{よって} \\[ 5pt ] &x^{\scriptsize{4}}-2x^{\scriptsize{3}}-x+8 \\[ 7pt ] &\quad = (2-x-2x^{\scriptsize{2}}) \left(-\frac{1}{2} x^{\scriptsize{2}}x+\frac{5}{4} x-\frac{9}{8} \right)-\frac{37}{8} x+\frac{41}{4} \end{align*}

分数が出てきたので、筆算をしていて不安に思ったかもしれませんが、間違っているわけではありません。

割られる式や割る式はどちらも整式なので、係数は整数となります。しかし、商や余りの係数に分数が出てくることもあります。

等式の右辺を展開して整理すると、ちゃんと左辺と同じ式になるはずです。計算結果が不安であれば、検算してみると良いでしょう。

整式の割り算では、上下に次数を揃えないせいでおかしな計算をしたり、係数の引き算を間違えたりすることが意外と起こります。自分がミスしやすそうな箇所に注意しながら演習を繰り返しましょう。

商や余りの係数が必ず整数になるとは限らない。