図形と方程式|放物線と円の共有点・接点について

今回は、放物線と円の共有点・接点について学習しましょう。
2つの図形の共有点や接点に関する問題は、入試でもよく出題されます。2つの図形の位置関係を把握できなければならないだけでなく、式の扱いにも慣れていなければならないからです。
図形の位置関係を把握するには、図示することが最も効果的です。しかし、日頃から作図の習慣がないと、自分にとって分かりやすい図を描くことはなかなか上手くできません。
習熟度が高くないと難しく感じるので、差をつけるには良い題材になる単元です。入試でもたびたび出題されるので、確実に解ける問題にしておいて得点源にしましょう。
放物線と円の共有点・接点
放物線とは、中学でも学習した2乗に比例する関数、いわゆる2次関数のグラフのことです。
対称の軸をもち、軸に関して左右対称なグラフになります。直線的なグラフではなく、曲線になります。日頃から図示する習慣がないと、意外と上手に描けないので注意しましょう。
ここでは、このような放物線と円との共有点や接点について学習します。
先ほども述べたように、放物線は左右対称な図形になります。円も左右対称な図形です。ほとんどの場合、放物線の軸が円の中心を通るので、円との共有点や接点は左右の2個でワンセットになるような結果が得られます。
もちろん、円に対する放物線の位置によっては必ずしも2個でワンセットになるとは限りません。それを把握するためにも、図示することはとても大切な作業になります。
放物線と円の共有点と2次方程式との関係
放物線と円の共有点は、放物線と円の方程式を連立したときの実数解から得られます。
放物線と円の方程式を連立すると、xまたはyについての2次方程式を導出することができます。放物線と円が共有点をもつ場合、2次方程式から実数解を得ることができます。この実数解が共有点の座標です。
また、放物線と円が共有点をもつ場合、2次方程式の解の判別式はD≧0を満たします。
放物線と円の接点と2次方程式との関係
放物線と円の接点も、放物線と円の方程式を連立したときの実数解から得られます。
共有点と異なるのは、放物線と円が接点をもつ場合、2次方程式の実数解は重解となることです。この重解が接点の座標です。
また、放物線と円が接点をもつ場合、2次方程式の解の判別式はD=0を満たします。
放物線と円の共有点や接点について大まかに把握できたら、次の例題を解いてみましょう。
放物線と円の共有点や接点を調べてみよう
次の例題を解いてみましょう。
例題
放物線 $y=-x^{2}+a$ と円 $x^{2}+y^{2}=4$ について、次のものを求めよ。
$(1) \quad$ この放物線と円が接するときの定数 $a$ の値
$(2) \quad$ $4$ 個の共有点をもつような定数 $a$ の値の範囲
例題(1)の解答・解説
例題(1)
放物線 $y=-x^{2}+a$ と円 $x^{2}+y^{2}=4$ について、次のものを求めよ。
$\quad$ この放物線と円が接するときの定数 $a$ の値
例題(1)では、放物線の式に含まれる定数aの値を求めます。ここでは「放物線と円が接する」という条件があります。
放物線と円が接するということは、放物線と円の方程式から得られる2次方程式が重解をもつということです。
また、2次方程式が重解をもつということは、解の判別式がD=0を満たすということです。これらの関係をしっかり把握しておきましょう。
まず、放物線と円の方程式を連立して、xまたはyについての2次方程式を導出します。
例題(1)の解答例 1⃣
\begin{align*} &\quad y=-x^{2}+a \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+y^{2}=4 \quad \cdots \text{②} \end{align*}①より
\begin{align*} &\quad y=-x^{2}+a \\[ 7pt ] &\quad x^{2}=-y+a \quad \cdots \text{③} \end{align*}③を②に代入すると
\begin{align*} \quad \left(-y+a \right)+y^{2}=4 \end{align*}整理すると
\begin{align*} \quad y^{2}-y+a-4=0 \quad \cdots \text{④} \end{align*}いつもの習慣でyを消去したくなりますが、xについて整理すると4次方程式になります。
せっかくyを消去できても、その後の式変形が難しくなります。式の取り扱いが楽になるように、xまたはyを消去しましょう。
xまたはyを消去するとき、式の次数ができるだけ上がらないようにしよう。
次は、2次方程式の解の判別式を利用するところですが、放物線と円が接する状況を考えてみましょう。
作図すると分かりますが、放物線と円が接するのは、2点で接する場合と1点で接する場合の2通りあります。
図なしで解こうとすると、たいていの場合、どちらかの場合が抜けてしまいます。
2次方程式が重解をもつ場合は、何個の点で接する場合か分かるでしょうか?
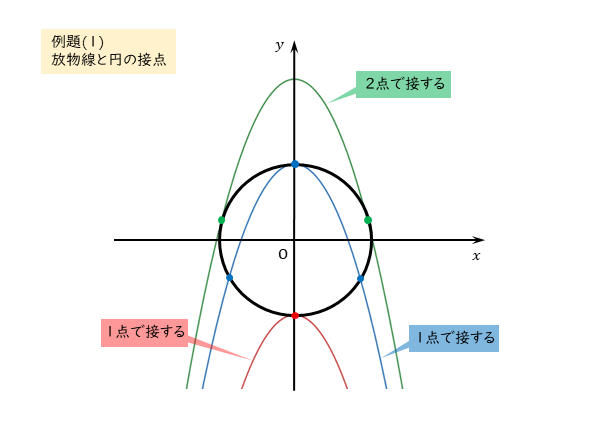
ここでは、yについての2次方程式を導出したので、この2次方程式が重解をもつ場合、実数解(yの値)は1個だけになるはずです。
つまり、図で言えば、放物線と円が2点で接する場合です。この場合、接点のy座標がともに同じになっていることが分かります。
ちなみに、放物線と円が1点で接する場合、2つの接点のy座標は異なっています。これは、yについての2次方程式が重解をもつ場合ではないことを表します。
以上のことを踏まえて解くとなると、場合分けになります。yについての2次方程式を利用する方から解いていきましょう。
例題(1)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y^{2}-y+a-4=0 \quad \cdots \text{④} \end{align*}$[1]$ 放物線と円が $2$ 点で接する場合
この場合、④は重解をもつので、④の判別式を $D$ とおくと
\begin{align*} \quad D &= \left(-1 \right)^{2}-4\left(a-4 \right) \\[ 7pt ] &= -4a+17 \end{align*}$D=0$ であるので
\begin{align*} \quad -4a+17=0 \end{align*}よって
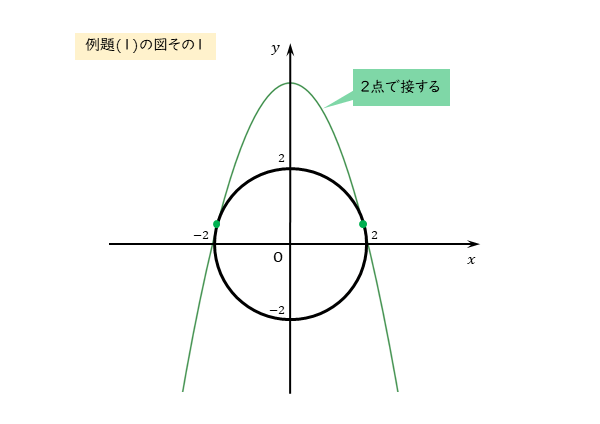
\begin{align*} \quad a= \frac{17}{4} \end{align*}放物線と円が2点で接する場合、図のような位置関係になります。
なお、定数aは、放物線の頂点のy座標です。また、頂点はy軸上にあります。
このことを踏まえると、解答例2⃣で求めたaの値は適切だろうと思われます。
放物線と円が1点で接する場合も忘れずに解きます。こちらは図があれば簡単に求めることができます。
例題(1)の解答例 3⃣
\begin{align*} \quad \vdots \end{align*}$[2]$ 放物線と円が $1$ 点で接する場合
図から
\begin{align*} \quad \left(0 \ , \ 2 \right) \ , \ \left(0 \ , \ -2 \right) \end{align*}で接するので
\begin{align*} \quad a = \pm 2 \end{align*}$[1] \ , \ [2]$ より求める $a$ の値は
\begin{align*} \quad a= \pm 2 \ , \ \frac{17}{4} \end{align*}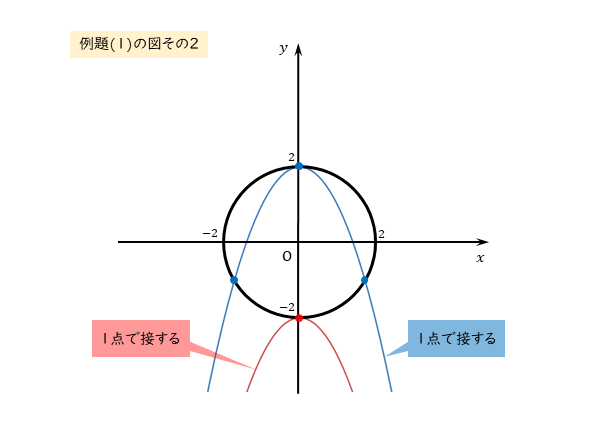
以上の解答例を推敲すると、以下のようになります。
例題(1)の解答例(推敲後)
\begin{align*} &\quad y=-x^{2}+a \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+y^{2}=4 \quad \cdots \text{②} \end{align*}①より
\begin{align*} \quad x^{2}=-y+a \end{align*}を②に代入すると
\begin{align*} \quad \left(-y+a \right)+y^{2}=4 \end{align*}よって
\begin{align*} \quad y^{2}-y+a-4=0 \quad \cdots \text{③} \end{align*}$[1]$ 放物線と円が $2$ 点で接する場合
この場合、③は重解をもつので、③の判別式を $D$ とおくと
\begin{align*} \quad D &= \left(-1 \right)^{2}-4\left(a-4 \right) \\[ 7pt ] &= -4a+17 \end{align*}$D=0$ より
\begin{align*} \quad -4a+17 &=0 \\[ 7pt ] \quad a &= \frac{17}{4} \end{align*}$[2]$ 放物線と円が $1$ 点で接する場合
図から
\begin{align*} \quad \left(0 \ , \ 2 \right) \ , \ \left(0 \ , \ -2 \right) \end{align*}で接するので
\begin{align*} \quad a = \pm 2 \end{align*}$[1] \ , \ [2]$ より求める $a$ の値は
\begin{align*} \quad a= \pm 2 \ , \ \frac{17}{4} \end{align*}
先に作図しておくと、ほとんど推敲の要らない答案を作成できるでしょう。
例題(2)の解答・解説
例題(2)
放物線 $y=-x^{2}+a$ と円 $x^{2}+y^{2}=4$ について、次のものを求めよ。
$\quad$ $4$ 個の共有点をもつような定数 $a$ の値の範囲
例題(2)では、定数aの値の範囲を求めます。ここでは「放物線と円が4個の共有点をもつ」という条件があります。
放物線と円が共有点を何個もつかは、作図すると分かります。作図するときのコツは、aの値に注意することです。
aの値によって、放物線の位置がy軸に沿って上下に移動します。
たとえば、aの値を小さいものから大きいものに順に変えてみましょう。その逆でも構いません。
放物線を下から上(または上から下)へ少しずつ移動させれば、共有点の個数をきちんと把握できるでしょう。
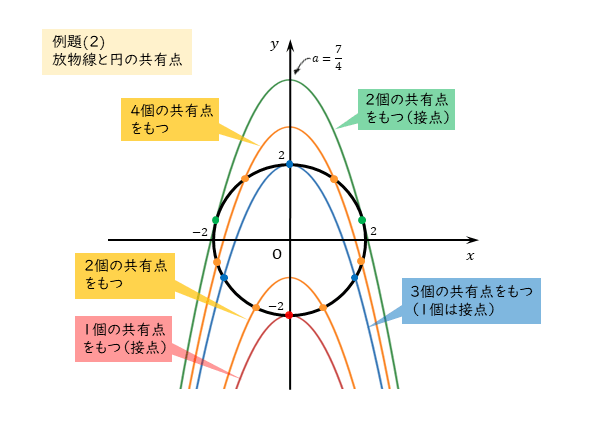
図から、放物線と円が4個の共有点をもつのは、放物線と円が3個の共有点をもつ場合と、2個の共有点をもつ場合との間です。
ここでは、放物線をy軸に沿って下から上へ平行移動しています。
放物線の頂点に注目した方が分かりやすいかもしれません。ここでは、頂点に注目して解いてみましょう。
例題(2)の解答例
放物線と円が $4$ 個の共有点をもつのは、図から、放物線の頂点が
\begin{align*} \quad \left(0 \ , \ 2 \right) \end{align*}から
\begin{align*} \quad \left(0 \ , \ \frac{17}{4} \right) \end{align*}を結ぶ線分上にあるときである。ただし、端点を除く。
よって
\begin{align*} \quad 2 \lt a \lt \frac{17}{4} \end{align*}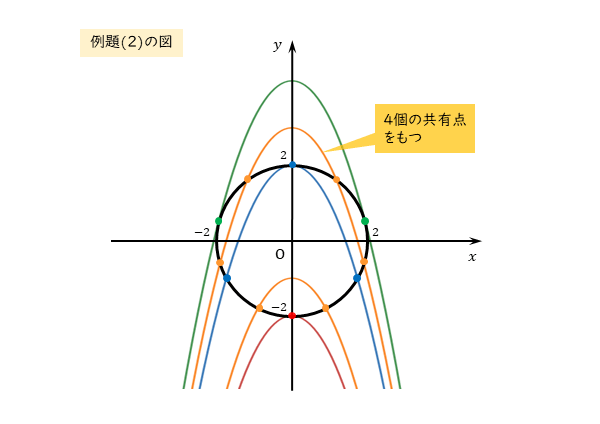
図と併せて考えれば、意外と簡単に解けます。
共有点⇔実数解
接点⇔重解
例題(2)の別解・解説
yについての2次方程式を利用して解いてみましょう。単純にD>0では解けないので注意が必要ですが、知っておいて損はないでしょう。
放物線と円の方程式を連立して、yについての2次方程式を導出します。
また、円の方程式を利用して、方程式が実数解をもつ範囲を導出します。
例題(2)の別解例 1⃣
\begin{align*} &\quad y=-x^{2}+a \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+y^{2}=4 \quad \cdots \text{②} \end{align*}①,②より
\begin{align*} \quad y^{2}-y+a-4=0 \quad \cdots \text{③} \end{align*}②より
\begin{align*} \quad x^{2}=-y^{2}+4 \geqq 0 \end{align*}であるので、不等式を解くと
\begin{align*} \quad -2 \leqq y \leqq 2 \end{align*}実数の範囲において、平方数が0以上となるのは明らかです。この性質は、整数の組を求める問題などでよく用いられるテクニックです。覚えておきましょう。
実数解となるyの値の範囲を求めたら、その範囲についてもう少し吟味します。
例題(2)の別解例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y^{2}-y+a-4=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad -2 \leqq y \leqq 2 \end{align*}ここで
\begin{align*} \quad -2 \lt y \lt 2 \quad \cdots \text{⑤} \end{align*}の $y$ の $1$ つの値に対して、$x$ の値は $2$ つある。
また
\begin{align*} \quad y= \pm 2 \end{align*}では、$x=0$ だけである。
よって、放物線と円が $4$ つの共有点をもつための条件は、③が⑤の範囲に異なる $2$ つの実数解をもつことである。
yについての2次方程式が異なる2つの実数解をもてば、それぞれのyの値につきxの値は2つずつあります。ですから、共有点は全部で2×2=4個になります。
理解が難しいかもしれませんが、三角関数などでも取り扱う内容なので、何度も反復して理解に努めましょう。
yについての2次方程式が異なる2つの実数解をもつ範囲内で、さらに条件を列挙します。このとき、yについての2次方程式から2次関数に置き換えて考えます。
例題(2)の別解例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y^{2}-y+a-4=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad -2 \lt y \lt 2 \quad \cdots \text{⑤} \\[ 7pt ] &\quad \vdots \end{align*}③の判別式を $D$ とすると
\begin{align*} \quad D= -4a+17 \gt 0 \end{align*}より
\begin{align*} \quad a \lt \frac{17}{4} \quad \cdots \text{⑥} \end{align*}ここで、③より
\begin{align*} \quad f(y) &=y^{2}-y+a-4 \\[ 7pt ] &= \left(y-\frac{1}{2} \right)^{2}+a-\frac{17}{4} \end{align*}とすると、軸は
\begin{align*} \quad -2 \lt \frac{1}{2} \lt 2 \end{align*}また
\begin{align*} \quad f(2)=-2+a \gt 0 \end{align*}から
\begin{align*} \quad a \gt 2 \quad \cdots \text{⑦} \end{align*}同様に
\begin{align*} \quad f(-2)=2+a \gt 0 \end{align*}から
\begin{align*} \quad a \gt -2 \quad \cdots \text{⑧} \end{align*}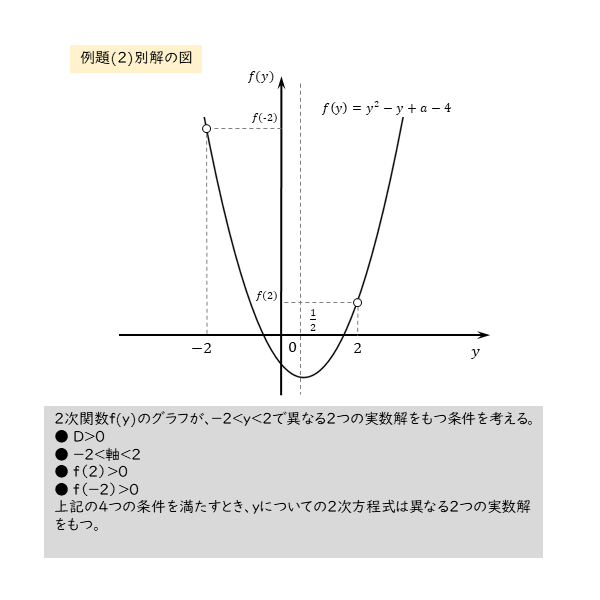
別解例3⃣も理解するのが難しいかもしれません。もともとの放物線で考えてしまうと混乱してしまいます。
別解例2⃣で、yについての2次方程式がもつ実数解のことを考えているので、それを踏まえての話になります。
列挙した条件の共通範囲を求めます。
例題(2)の別解例 4⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad a \lt \frac{17}{4} \quad \cdots \text{⑥} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a \gt 2 \quad \cdots \text{⑦} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a \gt -2 \quad \cdots \text{⑧} \end{align*}⑥~⑧の共通範囲を求めて
\begin{align*} \quad 2 \lt a \lt \frac{17}{4} \end{align*}xがyに置き換わっただけですが、いつもと異なる感覚になるかもしれません。文字に惑わされないように気を付けましょう。
次は、放物線と円の共有点・接点を扱った問題を実際に解いてみましょう。










