図形と方程式|放物線と円の共有点・接点について

放物線と円の共有点・接点を扱った問題を実際に解いてみよう
次の問を解いてみましょう。
問
放物線 $y=x^{2}$ と円 $x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0)$ がある。放物線と円の交点が $4$ 個となる $r$ の範囲を求めよ。
解く前に、放物線や円について基本的な事柄を確認しておきましょう。
放物線と円についての確認
放物線の方程式は
\begin{align*} \quad y=x^{2} \end{align*}より、頂点は原点で、軸は $y$ 軸。
また、円の方程式は
\begin{align*} \quad x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0) \end{align*}より、中心は $(0 \ , \ 4)$ 、半径は $r$。
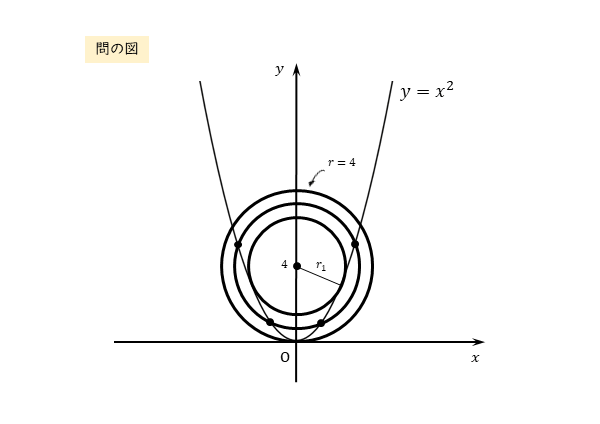
放物線も円もともに $y$ 軸に関して左右対称で、放物線の軸が円の中心を通る。
また、円の半径 $r$ の値が変化することで、放物線との交点の個数が変化する。
半径rの値が変化するのに伴って、放物線と円の交点の個数も変化します。rの値を徐々に大きくしていくと分かりやすいでしょう。
半径rの値を大きくすると、まず放物線が円と2点で接します(r=r1のとき)。
rの値をさらに大きくすると、放物線が円と4点で交わります。
最後に放物線が円と3点で交わります。このとき、接点が1つできます。
以上のことを踏まえて解きます。
問の解答例 1⃣
\begin{align*} &\quad y=x^{2} \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0) \quad \cdots \text{②} \end{align*}放物線と円が $1$ 点で接するときの円の半径は $4$ である。
また、放物線と円が $2$ 点で接するときの円の半径を $r_{1}$ とする。
放物線と円の交点が $4$ 個となるのは、図から
\begin{align*} \quad r_{1} \lt r \lt 4 \end{align*}のときである。
よって、$r_{1}$ の値を求めればよい。

求める半径rの範囲を把握することができました。あとは、放物線と円が2点で接するときの半径rの値を求めるだけです。
放物線と円の方程式を連立して、yについての2次方程式を導出します。yを消去すると、xについての4次方程式になるので注意しましょう。
問の解答例 2⃣
\begin{align*} &\quad y=x^{2} \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0) \quad \cdots \text{②} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad r_{1} \lt r \lt 4 \\[ 7pt ] &\quad \vdots \end{align*}①,②から $x$ を消去すると
\begin{align*} \quad y+(y-4)^{2}=r^{2} \end{align*}整理すると
\begin{align*} \quad y^{2}-7y+16-r^{2}=0 \end{align*}これに $r=r_{1}$ を代入すると
\begin{align*} \quad y^{2}-7y+16-{r_{1}}^{2}=0 \end{align*}放物線が円と2点で接する(r=r1)とき、yについての2次方程式は重解をもちます。2次方程式の判別式を利用します。
問の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad r_{1} \lt r \lt 4 \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad y^{2}-7y+16-{r_{1}}^{2}=0 \end{align*}この $2$ 次方程式の判別式を $D$ とすると、$r=r_{1}$ のとき $2$ 次方程式は重解をもつので
\begin{align*} \quad D &=\left(-7 \right)^{2}-4\left(16-{r_{1}}^{2} \right) \\[ 7pt ] &= 4{r_{1}}^{2}-15 =0 \end{align*}よって
\begin{align*} \quad {r_{1}}^{2}=\frac{15}{4} \end{align*}ここで、$r_{1} \gt 0$ より
\begin{align*} \quad r_{1}=\frac{\sqrt{15}}{2} \end{align*}したがって、求める $r$ の範囲は
\begin{align*} \quad \frac{\sqrt{15}}{2} \lt r \lt 4 \end{align*}図も参考にすると、放物線と円の交点の個数を把握しやすくなります。それほど悩まずに解くことができるでしょう。
問の別解・解説
例題(2)の別解と同様の考え方で解くことができます。もとの放物線と、後から導出した放物線(yについての2次式)とを混同しないように気を付けましょう。
問の別解例
\begin{align*} &\quad y=x^{2} \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0) \quad \cdots \text{②} \end{align*}①より
\begin{align*} \quad y=x^{2} \geqq 0 \end{align*}①であるので
\begin{align*} \quad y \geqq 0 \end{align*}$y \gt 0$ の $y$ の $1$ つの値に対して、$x$ の値は $2$ つある。
それに対して、$y=0$ のとき、$x$ の値は $x=0$ だけである。
よって、放物線と円が $4$ 個の共有点をもつための条件は、放物線①と円②から $x$ を消去して得られる $2$ 次方程式
\begin{align*} \quad y^{2}-7y+16-r^{2}=0 \end{align*}が $y \gt 0$ において、異なる $2$ つの正の解をもつことである。
y>0の範囲で考えなければならないので、「異なる2つの実数解」という条件では足りません。実数解は異なる2つの正の解でなければなりません。
このような解をもつ範囲内で、さらに条件を列挙します。このとき、yについての2次方程式から2次関数に置き換えて考えます。
問の別解例 2⃣
\begin{align*} &\quad y=x^{2} \quad \cdots \text{①} \\[ 7pt ] &\quad x^{2}+(y-4)^{2}=r^{2} \ (r \gt 0) \quad \cdots \text{②} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad y^{2}-7y+16-r^{2}=0 \\[ 7pt ] &\quad \vdots \end{align*}$2$ 次方程式の判別式を $D$ とすると
\begin{align*} \quad D &=\left(-7 \right)^{2}-4\left(16-r^{2} \right) \\[ 7pt ] &= 4r^{2}-15 \\[ 7pt ] &= \left(2r+\sqrt{15} \right)\left(2r-\sqrt{15} \right) \gt 0 \end{align*}ここで、$r \gt 0$ より
\begin{align*} \quad r \gt \frac{\sqrt{15}}{2} \quad \cdots \text{③} \end{align*}また
\begin{align*} \quad f(y) &=y^{2}-7y+16-r^{2} \\[ 7pt ] &=\left(y-\frac{7}{2} \right)^{2}+\frac{15}{4}-r^{2} \end{align*}とすると、軸は
\begin{align*} \quad \frac{7}{2} \gt 0 \end{align*}また
\begin{align*} \quad f(0) =16-r^{2} \gt 0 \end{align*}から
\begin{align*} \quad -4 \lt r \lt 4 \quad \cdots \text{④} \end{align*}③,④の共通範囲から、求める $r$ の範囲は
\begin{align*} \quad \frac{\sqrt{15}}{2} \lt r \lt 4 \end{align*}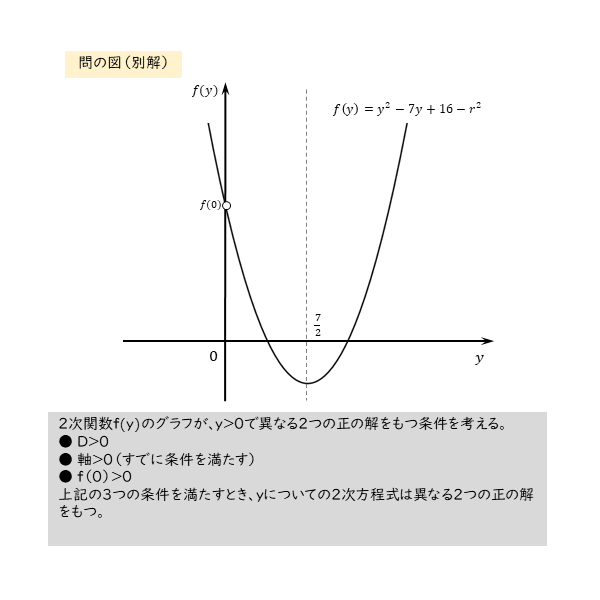
2次関数f(x)の式を変形すると、グラフの軸がy>0の範囲に含まれることが分かります。ですから、2次方程式が異なる2つの正の解をもつには、判別式D>0の条件と、f(0)>0の条件だけで済みます。
方程式の実数解と、グラフの共有点との関係は、関数の単元では頻繁に出題されます。特に、三角関数では2次関数よりも難解になるので、差がつきやすくなります。じっくり時間を取って余裕をもって取り組みましょう。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
共通テスト対策として必要なことをすべて備えた理想の予想問題集が完成
単に問題を解くだけでなく、その背景にある考え方や知識まで掘り下げて解説。「分析編」では、過去2回の試行調査(プレテスト)から見えてきた共通テストの出題傾向を詳細に分析するだけでなく、学習法や学習姿勢などの具体的な対策まで説明。本番でそのまま出そうな予想問題と、くわしい解説がセットになった至高の実践型問題集。
もくじ
- 本冊
- 分析編
- 解答・解説編
- 別冊
- 試行調査:2回分(2017年度/2018年度)
- 予想問題:2回分
公式サイトでは、一部の内容を閲覧できます。
KADOKAWAの公式サイト
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 放物線と円の接点は、2個の場合と1個の場合がある。
- 放物線と円の共有点を考えるとき、交わるだけでなく、接するときも考えよう。
- 放物線と円の接点を求めるには、yについての2次方程式を導出しよう。
- yについての2次方程式が重解をもてば、放物線と円は2点で接する。
- 共有点なら実数解、接点なら重解と覚えよう。












