数学Ｂ｜数列を扱った入試問題を解いてみよう

01/14/2023数学Ｂ

今回、紹介する問題は数列を扱ったものです。問題文から正確に分野を特定できた人はかなり演習をこなしていると言えます。

自分なりにじっくりと試行錯誤してみましょう。

過去問を解いてみよう

過去の入試問題なので、それなりに難易度は高いです。まずは力試しに自力で解いてみましょう。

自力で解けない場合、以下の「問題を解く前に」がヒントになります。

問題を解く前に

方針を決めよう

マーク形式レベルであれば、 ほとんどの場合で問題を一読すると方針が１つに決まるので、すぐに取り掛かれます。

それに対して、記述形式レベル（２次試験レベル）になると、方針の候補が１つとは限らない問題が多くなります。分野を横断した問題が増えるからです。

そうなると、できるだけ効率良く解ける方針を採用しなければなりません。記述形式レベルを問題を解くには、記述する前に方針をきちんと決めることがとても大切になります。

図形問題であれば、図を見ながら方針を考えていくことになります。

樹形図を描いてみよう

色の塗り分け問題なので、「数列」ではなく、「場合の数」だろうと突っ込みが入りそうです。たしかに問題の指示通り、場合の数を考える問題です。ですから、まずは樹形図を描きながら考えてみましょう。

１両目と２両目の色の組合せを考えてみましょう。色の組合せは以下のようになるはずです。

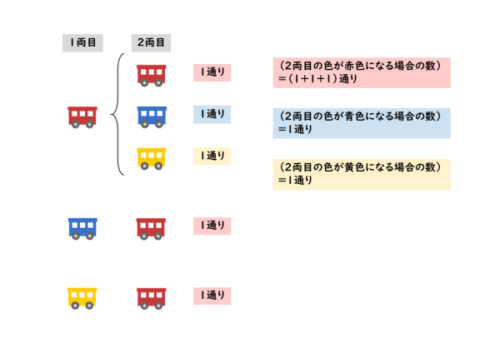
上図は樹形図っぽくないですが、色の組合せは分かります。

色の塗り方を考えなければならないので、色ごとに注目します。２両目の色の種類ごとに場合の数を調べます。

２両目が赤色になる場合では、１両目がどの色についても１通りずつあるので合計３通りです。２両目が青色または黄色になる場合では、１両目が赤色の場合にそれぞれ１通りあります。

樹形図でパターンを知ろう

３両目以降も考えていくと、色の組合せのパターンが徐々に分かってきます。３両目の色の種類ごとに場合の数を調べます。

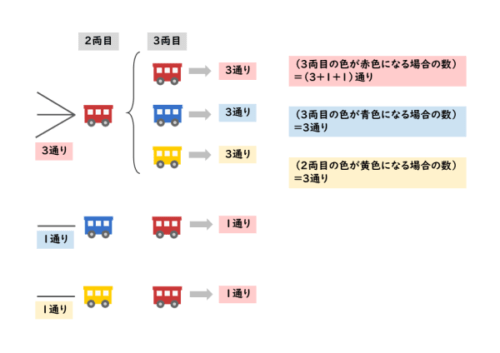
たとえば、３両目が青色となるのは、２両目が赤色のときです。２両目が赤色の場合は３通りありました。ですから、２両目が赤色で、３両目が青色となる場合の数は、積の法則から３×１×１＝３通りあります。

積の法則で計算しましたが、単純に考えてみると、２両目の色における場合の数が、そのまま３両目における場合の数になっていることに気付きます。直前の車両における場合の数を把握しておくことが必要です。

同じようにして調べていくと、色ごとの場合の数は以下のようになります。

場合の数を調べる際には、１両目からが基本ですが、３両目から１両目に向かって逆に数える方が数えやすいかもしれません。

場合の数が定まらなければ文字で表そう

４両目以降も同じ要領で調べていけば、場合の数をその都度求めることができます。しかし、問題では何両目までと特定されていないので、このやり方を続けても、場合の数を具体的な値で表すことができません。

それでも４両目、５両目……と樹形図を描き続けて、場合の数の移り変わりを調べたいところです。イメージが湧かない場合や何らかの規則性が得られない場合、手を動かすべきです。

ここでは、何らかの規則性が得られたとして、気付いたことを整理してみます。

これらを参考にして、場合の数を具体的な値ではなく、文字で表すことを考えます。「ｎ両目」とあるので、どうやっても具体的な値で場合の数を得ることはできないからです。

隣り合う車両のうち、前の車両の色についての場合の数が分かっていれば、後ろの車両の色についての場合の数が分かることを利用します。

このことをｎ両目とｎ＋１両目にも適応させます。ここまでくると、数列、特に漸化式を扱った問題でもあることに気付くかもしれません。