確率|条件つき確率について

今回は条件つき確率について学習しましょう。入試では頻繁に出題されているので、今後も出題されると考えておいた方が無難です。しっかりマスターしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
条件つき確率、乗法定理の定義
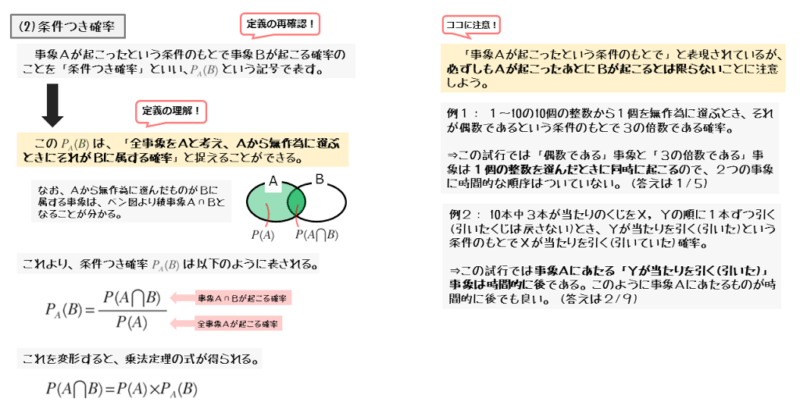
条件つき確率とは、2つの事象A,Bについて、Aが起こったという条件のもとでBが起こる確率のことです。このAが起こったという条件のもとでBが起こる条件つき確率のことをPA(B)と表します。
また、2つの事象A,Bがともに起こる積事象の確率P(A⋂B)は、Aが起こる確率P(A)とAが起こったという条件のもとでBが起こる条件つき確率PA(B)との積で表されます。これを乗法定理と言います。
乗法定理
事象 $A$ が起こる確率を $P(A)$、事象 $B$ が起こる確率を $P(B)$ とする。
$2$ つの事象 $A \ , \ B$ がともに起こる積事象の確率 $P(A \cap B)$ は、$A$ が起こる確率 $P(A)$ と $A$ が起こったという条件のもとで $B$ が起こる条件つき確率 $P_{A}(B)$ との積で表される。
\begin{align*} \quad P \left( A \cap B \right) = P(A) \times P_{A} \left( B \right) \end{align*}式や記号を見れば、条件つき確率PA(B)と積事象が起こる確率P(A⋂B)とが異なるものだと分かります。
しかし、入試レベルの問題では、これらを区別するのは単なる暗記だと少々難しいです。たくさんの演習をこなして、2つの違いをしっかりと理解することが大切です。入試レベルの問題でもきちんと区別できるようにしておきましょう。
条件つき確率を求めよう
特定の事象を全事象に見立てる
事象Aが起こったという条件のもとで事象Bが起こる確率のことを条件つき確率PA(B)と言います。この「事象Aが起こったという条件のもと」の部分がポイントです。
「事象Aが起こったという条件のもと」ということなので、事象Aの中だけで考えれば良いということになります。言い換えると、事象Aが全事象となったと捉えることができます。
このように全事象に見立てた特定の事象から無作為に選ぶときの話が条件つき確率の話になります。このことを理解しているだけでもかなり違います。普段の全事象Uとは異なるので注意しましょう。
条件つき確率では、事象Aを全事象に見立てて考えるのがポイント。
2つの事象に共通な事象は積事象
以上のことから、条件つき確率PA(B)は、全事象に見立てた事象Aから無作為に選んだものがBに属する確率と捉えることができます。
ところで、事象Aから無作為に選んだものが事象Bにも属するというのは、言い換えれば、事象A,Bがともに起こる積事象A⋂Bに属するということです。このことはベン図を見れば明らかです。
また、要素に注目すると、「事象Aが起こったという条件のもとで事象Bが起こる」というのは、「事象Aに属する要素の中で、事象Bにも属する要素である」ということです。
ですから、条件つき確率では、一方の事象の中で無作為に選んだ要素が、他方の事象にも属する共通の要素である確率を求めていることが分かります。
このことから、事象Aが起こったという条件のもとで事象Bが起こる条件つき確率PA(B)は以下のような式で表されます。
条件つき確率PA(B)
事象 $A$ の要素の個数を $n(A)$、$2$ つの事象 $A \ , \ B$ がともに起こる積事象の要素の個数を $n(A \cap B)$ とする。
$A$ が起こったという条件のもとで $B$ が起こる条件つき確率 $P_{A}(B)$ は
\begin{align*} \quad P_{A} \left( B \right) &= \frac{n \left( A \cap B \right)}{n \left( A \right)} \\[ 10pt ] &= \cfrac{ \cfrac{n \left( A \cap B \right)}{n \left( U \right)} }{ \cfrac{n \left( A \right)}{n \left( U \right)} } \\[ 10pt ] &= \frac{P \left( A \cap B \right)}{P(A)} \end{align*}確率は場合の数で求めるのが基本ですが、条件つき確率でも同じように求めることができます。最初のうちは、各事象の要素から条件つき確率を求める方が簡単で理解しやすいと思います。
また、2~3行目のように、分母と分子を全事象Uの場合の数n(U)でそれぞれ割ると、確率を用いて表すこともできます。
確率を用いる場合に注意したいのは、全事象Uに対する事象Aや積事象A⋂Bが起こる確率を用いることです。記号の意味を理解し、慣れてきたら、確率の方でも解いてみると良いでしょう。
なお、両辺にP(A)を掛けると、乗法定理の式を導出できます。
条件つき確率では時間的な順序は関係ない
学習したての頃によく間違えるのは「事象Aが起こったという条件のもとで」という表現の取り扱いです。
この表現から「事象Aが先に起こり、その後に事象Bが起こる(起こらなければならない)」と解釈しがちです。このような解釈のままでいると、条件つき確率を扱った問題を解けるようにはなりません。
実は、事象Aが起こったあとに事象Bが起こるとは限らない場合があります。2つの事象A,Bには時間的な順序は関係ないことに注意しましょう。
具体例をいくつか見てみましょう。
条件つき確率の具体例その1
1~10の10個の整数から1個を無作為に選ぶとき、それが偶数であるという条件のもとで3の倍数である確率。
10個の整数から1個を選ぶ試行は1回だけです。ですから、選んだ整数が偶数である事象と、選んだ整数が3の倍数である事象とは同時に起こっています。2つの事象に時間的な順序がついていないことが分かります。
条件つき確率の具体例その2
10本中3本が当たりのくじをX,Yの順に1本ずつ引くとき、Yが当たりを引く(引いた)という条件のもとでXが当たりを引く(引いていた)確率。ただし、引いたくじは戻さない。
X,Yの2人が順番にくじを引くので、2つの試行には時間的に順番がついています。しかし、事象Aに相当するのは、Yが当たりを引く(引いた)事象です。これは、2回目の試行における事象です。
このように事象Aに相当するものが時間的に後の結果であっても問題ありません。時間的な順序は無視するようにしましょう。
これまでをまとめると以下のようになります。
各種の確率の混同に注意しよう
学習したての頃は、各種の確率P(A),P(A⋂B),PA(B)をよく混同しやすいので注意しましょう。
それぞれの違いは、ベン図を利用するとよく理解することができます。字面だけでなく、図解しながら学習しましょう。
事象に属する要素(根元事象)に注目して違いをまとめると以下のようになります。
用語の違いを理解しよう
- 事象Aが起こるP(A) … 全事象Uの中から無作為に選んだ要素が、事象Aに属する確率
- 積事象が起こるP(A⋂B) … 全事象Uの中から無作為に選んだ要素が、積事象A⋂Bに属する確率
- 条件つき確率PA(B) … 事象Aの中から無作為に選んだ要素が、事象Bに属する確率
これまで扱ってきた確率では、全事象はすべての根元事象を含む事象Uでした。しかし、条件つき確率だと違います。
全事象となるのは、事象AやBなどの特定の事象です。この違いを押さえておけば、条件つき確率をマスターするのも早いでしょう。
次は、条件つき確率を扱った問題を実際に解いてみましょう。