図形と方程式｜折れ線の長さの最小について

01/14/2023数学２

折れ線の長さの最小を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

直線ℓ： $y=\frac{1}{2}x+1$ と $2$ 点 $A(1 \ , \ 4) \ , \ B(5 \ , \ 6)$ がある。

直線ℓ上の点 $P$ で、 $AP+PB$ を最小にする点 $P$ の座標を求めよ。

問の解答・解説

例題のときと直線の方程式や点の座標が変わっているだけです。例題と同じ方針で取り組みましょう。

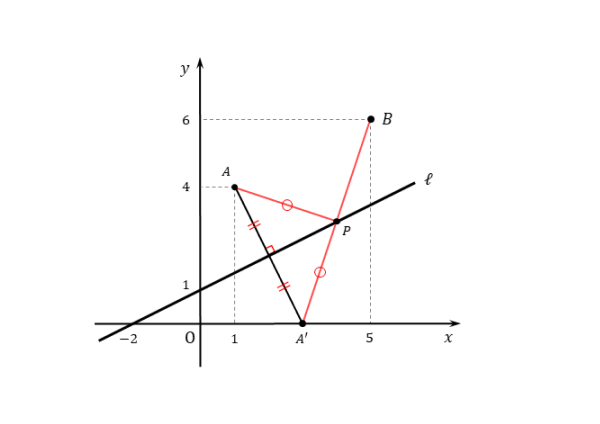
作図は以下の通りです。丁寧に作図すれば、点Ａ’や点Ｐの位置が大まかに把握できます。

２点Ａ，Ｂが直線に関して同じ側にあるので、点Ａと線対称な点Ａ’をとり、その座標を求めます。

このとき、２直線の垂直条件や中点の座標を利用します。

また、直線ＡＡ’がｘ軸と垂直でないことに言及しておきましょう。

問の解答例 1⃣

直線ℓについて

$\begin{align*} \quad y=\frac{1}{2}x+1 \ \cdots \text{①} \end{align*}$

とする。

また、直線ℓに関して $A$ と対称な点を

$\begin{align*} \quad A'(a \ , \ b) \end{align*}$

とする。

直線 $AA’$ は $x$ 軸に垂直ではないので

$\begin{align*} \quad a \neq 1 \end{align*}$

$AA’ \perp$ ℓであるので

$\begin{align*} \quad \frac{b-4}{a-1} \cdot \frac{1}{2}=-1 \end{align*}$

整理すると

$\begin{align*} \quad 2a+b=6 \quad \cdots \text{②} \end{align*}$

線分 $AA’$ の中点が直線ℓ上にあるので

$\begin{align*} \quad \frac{b+4}{2}=\frac{1}{2} \cdot \frac{a+1}{2}+1 \end{align*}$

整理すると

$\begin{align*} \quad a-2b=3 \quad \cdots \text{③} \end{align*}$

②，③を解くと

$\begin{align*} \quad a=3 \ , \ b=0 \end{align*}$

よって、点 $A’$ の座標は

$\begin{align*} \quad A’ \ (3 \ , \ 0) \end{align*}$

座標の計算結果と図とを見比べてみても問題なさそうです。点Ａ’の座標が分かったので、点Ｐの位置を決めます。

点Ａ’から点Ｐを経由して点Ｂへたどる経路を考えます。この経路が最短となるのは３点Ａ’，Ｐ，Ｂが同じ直線上にあるときです。

このことから、点Ｐが直線Ａ’Ｂ上にあるとき、折れ線の長さが最小となります。

問の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad A’ \ (3 \ , \ 0) \end{align*}$

このとき

$\begin{align*} \quad AP+PB=A’P+PB \geqq A’B \end{align*}$

よって、 $3$ 点 $A’ \ , \ P \ , \ B$ が同じ直線上にあるとき、 $AP+PB$ は最小になる。

点Ｐは直線ℓ上にあるだけではなく、線分Ａ’Ｂ上にもあります。ですから、点Ｐは線分Ａ’Ｂと直線ℓの交点です。

直線Ａ’Ｂの方程式を求め、交点の座標を求めます。

問の解答例 3⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=\frac{1}{2}x+1 \ \cdots \text{①} \\[ 7pt ] &\quad \vdots \end{align*}$

直線 $A’B$ の方程式は、 $2$ 点

$\begin{align*} \quad A'(3 \ , \ 0) \ , \ B(5 \ , \ 6) \end{align*}$

を通るので

$\begin{align*} \quad \left(6-0 \right) \left(x-5 \right)-\left(5-3 \right) \left(y-6 \right)=0 \end{align*}$

すなわち

$\begin{align*} \quad 6\left(x-5 \right)-2\left(y-6 \right)=0 \end{align*}$

よって

$\begin{align*} \quad y=3x-9 \quad \cdots \text{④} \end{align*}$

直線 $A’B$ と直線ℓの交点を $P_{0}$ とすると、その座標は①を④に代入して

$\begin{align*} \quad \frac{1}{2}x+1=3x-9 \end{align*}$

これを解くと

$\begin{align*} \quad x=4 \end{align*}$

これと④より

$\begin{align*} \quad y=3 \end{align*}$

よって

$\begin{align*} \quad P_{0} \ (4 \ , \ 3) \end{align*}$

したがって、 $AP+PB$ を最小にする点 $P$ の座標は

$\begin{align*} \quad (4 \ , \ 3) \end{align*}$

２点を通る直線の方程式には、２通りの表し方があります。できるだけ分数を使わない表し方に慣れておきましょう。

直線の方程式

$2$ 点 $(x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2})$ を通る直線の方程式

$\begin{align*} \quad y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \left( x-x_{1} \right) \quad \cdots \text{①} \end{align*}$

ただし

$\begin{align*} \quad x_{2} \neq x_{1} \end{align*}$

または

$\begin{align*} \quad \left( y_{2}-y_{1} \right) \left( x-x_{1} \right)-\left( x_{2}-x_{1} \right) \left( y-y_{1} \right)=0 \quad \cdots \text{②} \end{align*}$

これは

$\begin{align*} \quad x_{2}=x_{1} \end{align*}$

のときも含む。

②式は、①式と異なり、すべての直線を表せます。優先的に覚えるのであれば、②式にしましょう。

長さの最小を考えるので、折れ線から線分にすることがポイントです。このことが分かっていれば、求めたい点Ｐの位置はすぐに分かります。

ただし、点Ｐの座標を求めるには、直線について学習してきたことを適切に使い分ける必要があります。色々な事柄を組み合わせて解くので、１つ１つの事柄をしっかりマスターしておくことが大切です。

Recommended books

さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。

難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。

傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。

おすすめ

ここで紹介する問題集は、『大学入試全レベル問題集数学』シリーズです。昔からある有名なレベル別問題集です。

３年の１学期までに基礎レベル１を解いて、教科書内容の補完をしてしまいましょう。夏休みになったら、共通テストレベル２で実戦練習をこなすと良いでしょう。９月～１０月くらいまでにこの２冊を何度も周回して仕上げれば、秋からの２次対策にスムーズに移行できるでしょう。

なお、新入試に対応するための改訂版が２０２０年２月に出版されています。改訂版を希望する場合、「新入試対応」とあるものを購入しましょう。

◆特長◆

大学入試の基本となる問題を扱った問題集です。問題数は１３８問です。

問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。

問題編冊子４４頁、解答編冊子２２４頁の構成となっています。

◆自分にあったレベルが選べる！◆

基礎レベル

共通テストレベル

私大標準・国公立大レベル

私大上位・国公立大上位レベル

私大標準・国公立大レベル

私大上位・国公立大上位レベル