場合の数｜場合の数について

11/27/2021数学Ａ

今回は「場合の数」についてです。中学で学習した内容を基礎として、新たな用語や法則などを学習します。１つ１つしっかりマスターしながら進めていきましょう。

記事の画像が見辛いときはクリックすると拡大できます。

場合の数を漏れなく、重複なく数え上げよう

場合の数とは、ある事柄において起こり得るすべての場合の総数のことです。

たとえば「サイコロの出目の組合せ」や「コインの表裏の組合せ」などの場合の数を扱います。

このような場合の数を調べるためには、起こり得るすべての場合を漏れなく、そして重複なく数え上げる必要があります。

樹形図を使って場合の数を調べよう

場合の数を調べるとき、漏れや重複に注意しなければなりません。しかし、頭の中だけで場合の数を数え上げるのは難しいときがほとんどです。漏れや重複を防ぐために、視覚化して調べるのが一般的です。

視覚化する方法として、樹形図を使うのが一般的です。考え得る場合を書き出していくと、枝分かれしたような図になるので、樹形図と呼ばれます。

樹形図を書いても漏れや重複が出てくることがあります。そのようなことが起こるのは、思いつきで書き出していることがほとんどです。

漏れや重複を防ぐために樹形図を使うのですから、思いつきではなく、順序良く書き出すことが大切です。

和の法則と積の法則を使って数え上げよう

樹形図を使えば場合の数を求めることができます。そうは言っても、問題によっては場合の数が多くなることがあります。場合の数が何百通りもあれば、樹形図を書くのもさすがに難しくなります。

そういうとき、和の法則や積の法則などを上手に利用すると、場合の数を簡単に求めることができます。

２つの事柄Ａ，Ｂが同時に起こらないとき、事柄Ａまたは事柄Ｂの起こる場合の数は、事柄Ａと事柄Ｂの場合の数の和で求めることができます。これが和の法則です。「２つの事柄Ａ，Ｂが同時に起こらない」という点が大切です。

また、事柄Ａが起こる場合の数のそれぞれについて、事柄Ｂが起こる場合が同じ数ずつあるとき、事柄Ａと事柄Ｂがともに起こる場合の数は、事柄Ａと事柄Ｂの場合の数の積で求めることができます。これが積の法則です。

樹形図を利用するのが物理的に難しいとき、和の法則や積の法則を利用して場合の数を調べましょう。ただし、和の法則や積の法則を使える条件かどうかをしっかり確認しましょう。

場合の数の調べ方は、主に３パターンあります。このうち和の法則や積の法則を使う方法では、計算で場合の数を求めるので、考え方が間違っていると漏れや重複が出てきます。注意しましょう。

これまでの用語についてまとめると以下のようになります。

和の法則の使い方

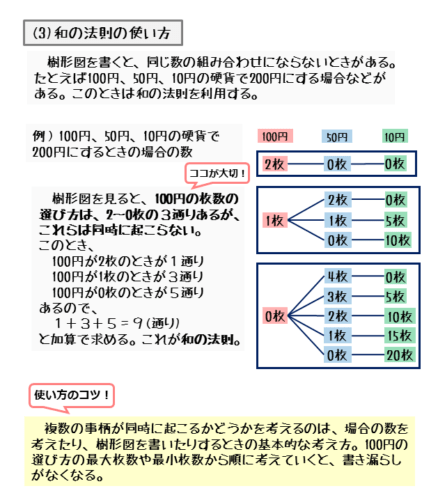
「１００円、５０円、１０円の硬貨を何枚か組み合わせて２００円にする場合」について考えてみましょう。

２００円になる硬貨の組合せを考えれば、場合の数を求めることができます。１００円の枚数に注目すると、その枚数は２，１，０枚の３通りが考えられます。

これらの場合を事柄Ａ，Ｂ，Ｃとすると、１００円の枚数が同時に１枚になったり、２枚になったりすることはないので、３つの事柄Ａ，Ｂ，Ｃは同時に起こりません。

また、２００円にするのに、１００円の枚数は２枚であっても１枚であってもよいので、事柄Ａまたは事柄Ｂまたは事柄Ｃが起こる場合の数が、求めたい場合の数になります。このような場合に和の法則を利用できます。

難しいと感じるかもしれませんが、樹形図で判断できるので、まずは樹形図をしっかり書きましょう。樹形図では、２００円になる硬貨の組合せを順序良く書き出していきましょう。

樹形図ではありませんが、以下のように表にまとめることもできます。１００円の枚数を最大の２枚から順に減らしていき、硬貨の組合せを書き出します。

１００円硬貨が２枚（事柄Ａ）のとき、硬貨の組合せは１通りだけです。

また、１００円硬貨が１枚（事柄Ｂ）のとき、硬貨の組合せは３通りあります。さいごに１００円硬貨が０枚（事柄Ｃ）のとき、硬貨の組合せは５通りあります。

１００円硬貨の枚数が２，１，０枚になる場合は同時に起こらないので、和の法則を使って場合の数を求めます。

樹形図だと以下のようになります。

樹形図を見ると、３つの事柄Ａ，Ｂ，Ｃが同時に起こらないので、それに対応して３つの樹ができます。樹が複数あれば、同時に起こらない事柄があるということです。

このように和の法則が使えるかどうかは、樹形図から判断できます。

同時に起こらない事柄があれば、樹形図では事柄の数に応じて独立した樹ができます。樹形図にはこのような使い方もあることを知っておきましょう。

積の法則の使い方

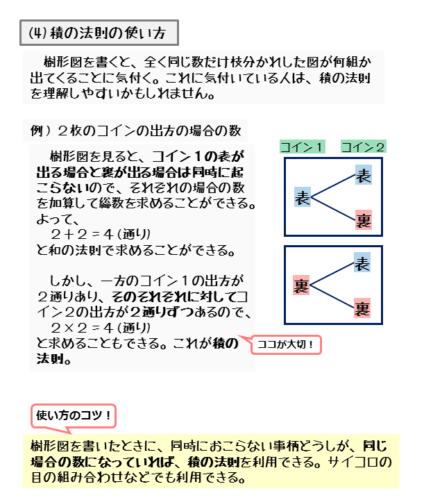
たとえば、２枚のコインを振ったとき、一方のコインの出方は表と裏の２通りあります。その出方のそれぞれについて、他方のコインの出方は表と裏の２通りずつあります。

このような場合、積の法則で場合の数を求めることができます。

樹形図は以下のようになります。樹形図を見ると、表が出る事柄と裏が出る事柄は同時に起こらないので、樹が２つできています。

先ほどの硬貨の例と大きく異なるのは、どちらの樹も同じ数だけ枝分かれしているという点です。これは、一方のコインの出方のそれぞれについて、他方のコインの出方が同じ数ずつあるからです。

このような樹形図ができたとき「事柄Ａの起こり方のそれぞれについて、事柄Ｂの起こり方が同じ数ずつある」状態を表しています。

樹形図を描いて分かることをまとめると以下のようになります。

樹形図から分かることを知っていれば、和の法則や積の法則の使いどころが分かります。

樹が複数できた時点で和の法則を利用することになりますが、特に枝数が同じ樹ができていれば、和の法則ではなく、積の法則を利用します。

今後は場合の数が多い問題を扱うことが多くなるので、樹形図を掛けなくても判断できるようにしておきましょう。

次は実際に問題を解いてみましょう。