場合の数|場合の数について

和の法則や積の法則を扱った問題を解いてみよう
次の問題を考えてみましょう。
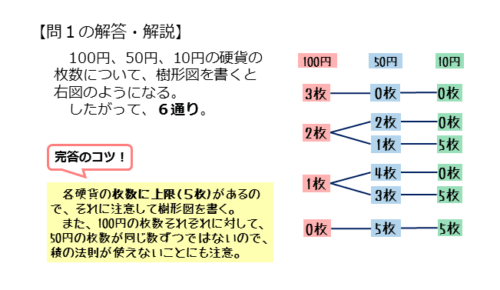
問1の解答・解説
問1
$100$ 円、$50$ 円、$10$ 円の硬貨がそれぞれ $5$ 枚ずつある。これらを用いて $300$ 円の支払い方は何通りあるか。
100円硬貨の枚数に注目して、枚数の組合せを漏れなく重複なく書き出します。ただし、それぞれの硬貨は5枚が上限です。
問1の解答例 1⃣
$100$ 円の枚数に注目して、枚数の組合せを考える。
組合せを表にまとめると以下のようになる。
\begin{align*} \begin{array}{c|ccc} {\scriptsize \text{硬貨}} & 100 & 50 & 10 \\ \hline {\scriptsize \text{事柄 $A$}} & 3 & 0 & 0 \\ \hline {\scriptsize \text{事柄 $B$}} & 2 & 2 & 0 \\ & 2 & 1 & 5 \\ \hline {\scriptsize \text{事柄 $C$}} & 1 & 4 & 0 \\ & 1 & 3 & 5 \\ \hline {\scriptsize \text{事柄 $D$}} & 0 & 5 & 5 \end{array} \end{align*}100円硬貨の枚数は、3,2,1,0枚の4通り考えられます。これらは同時に起こらない事柄なので、樹形図であれば、独立した樹が4つできます。
それぞれの樹の枝数は、100円硬貨の枚数によって変わるので、すべてが同じ枝数の樹になりません。積の法則が使えないので、和の法則を使って場合の数を求めます。
問1の解答例 2⃣
$100$ 円の枚数に注目して、枚数の組合せを考える。
組合せを表にまとめると以下のようになる。
\begin{align*} \begin{array}{c|ccc} {\scriptsize \text{硬貨}} & 100 & 50 & 10 \\ \hline {\scriptsize \text{事柄 $A$}} & 3 & 0 & 0 \\ \hline {\scriptsize \text{事柄 $B$}} & 2 & 2 & 0 \\ & 2 & 1 & 5 \\ \hline {\scriptsize \text{事柄 $C$}} & 1 & 4 & 0 \\ & 1 & 3 & 5 \\ \hline {\scriptsize \text{事柄 $D$}} & 0 & 5 & 5 \end{array} \end{align*}表より、$100$ 円の枚数が $3$ 枚になる組合せは $1$ 通り、$2$ 枚になる組合せは $2$ 通り、$1$ 枚になる組合せは $2$ 通り、$0$ 枚になる組合せは $1$ 通りある。
したがって、求める場合の数は和の法則より
\begin{align*} \quad 1+2+2+1=6 \ \text{(通り)} \end{align*}樹形図を利用した解答例は以下のようになります。
「硬貨を用いて~円にする」という問題では、硬貨の枚数の組合せを樹形図で表します。このとき、独立した樹が複数できます。
枝の数がどの樹も同じであれば積の法則を利用しますが、本問のように異なれば和の法則を利用して場合の数を求めます。
硬貨の枚数の組合せは、和の法則を利用して求める。樹形図を描くと、独立した樹(同時に起こらない複数の事柄)が複数できる。
問2の解答・解説
問2
大小 $2$ 個のサイコロを投げたとき、目の和が $5$ の倍数になるのは、何通りあるか。
目の和が5の倍数になるのは、和が5,10になるときです。サイコロ(大)の目に注目して順序良く組合せを書き出します。
問2の解答例 1⃣
目の和が $5$ の倍数になるのは、和が $5 \ , \ 10$ になるとき。
このとき、大のサイコロに注目した出目の組合せを考える。
組合せを表にまとめると以下のようになる。
\begin{align*} \begin{array}{c|cc} {\tiny \text{サイコロ}} & {\tiny \text{大}} & {\tiny \text{小}} \\ \hline {\scriptsize \text{事柄 $1$}} & 1 & 4 \\ \hline {\scriptsize \text{事柄 $2$}} & 2 & 3 \\ \hline {\scriptsize \text{事柄 $3$}} & 3 & 2 \\ \hline {\scriptsize \text{事柄 $4$}} & 4 & 1 \\ & 4 & 6 \\ \hline {\scriptsize \text{事柄 $5$}} & 5 & 5 \\ \hline {\scriptsize \text{事柄 $6$}} & 6 & 4 \end{array} \end{align*}上の表では、大サイコロの目に注目したので、大サイコロの目のぶんだけ事柄(6つ)があります。樹形図であれば、樹が6つできるはずです。
大サイコロの出目は1~6の6通りありますが、これらは同時に起こりません。和の法則を利用して場合の数を求めます。
問2の解答例 2⃣
目の和が $5$ の倍数になるのは、和が $5 \ , \ 10$ になるとき。
このとき、大のサイコロに注目した出目の組合せを考える。
組合せを表にまとめると以下のようになる。
\begin{align*} \begin{array}{c|cc} {\tiny \text{サイコロ}} & {\tiny \text{大}} & {\tiny \text{小}} \\ \hline {\scriptsize \text{事柄 $1$}} & 1 & 4 \\ \hline {\scriptsize \text{事柄 $2$}} & 2 & 3 \\ \hline {\scriptsize \text{事柄 $3$}} & 3 & 2 \\ \hline {\scriptsize \text{事柄 $4$}} & 4 & 1 \\ & 4 & 6 \\ \hline {\scriptsize \text{事柄 $5$}} & 5 & 5 \\ \hline {\scriptsize \text{事柄 $6$}} & 6 & 4 \end{array} \end{align*}表より、求める場合の数は和の法則より
\begin{align*} \quad 1+1+1+2+1+1=7 \ \text{(通り)} \end{align*}大サイコロの出目を事柄にしましたが、これに対して、目の和を事柄として考えることもできます。この場合、目の和が5の場合と10の場合の2つの事柄になります。
どちらの考え方でも構いませんが、視点が変われば事柄の数が変わるので注意しましょう。
サイコロを扱った問題では、目の組合せよりも、目の和や積などが必要になることが多いです。このような場合、一覧表にまとめた方が分かりやすくなります。
サイコロの出目の和
\begin{align*} \begin{array}{c|cccccc} {\tiny \text{小}} \ \backslash \ {\tiny \text{大}} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ 6 & 7 & 8 & 9 & 10 & 11 & 12 \end{array} \end{align*}縦と横に大小のサイコロの目を書き、表の中には目の和を書き込んでいきます。目の和を調べるので、目の組合せだけでは足りません。ですから、今回は樹形図よりも一覧表の方が適しています。
表を見ると5または10が全部で7個あるので、5の倍数になる目の組合せは7通りになります。
一覧表を利用した解答例は以下のようになります。
サイコロを扱った問題では、目の組合せ自体が必要であれば樹形図だけも足りるでしょう。しかし、目の和や積であれば、樹形図よりも一覧表の方が使い勝手が良いでしょう。
コインを扱った問題では、樹形図よりも表を利用しよう。表を使うとき、場合の数は、和の法則や積の法則を利用せずに数え上げるだけ。
Recommended books
単元ごとに得意・不得意がある場合、短期間で学習できる教材があると便利です。
オススメその1
1冊目は『これならわかる! 図解 場合の数と確率』です。
図が豊富で丁寧に解説されています。また、問題も多く扱っているので、演習不足にならないでしょう。
重複なく、漏れがないように数えるための考え方、数え方の基本をマスターできる教材です。
以下、2冊は短期間で学習するのに適した問題集です。場合の数や確率について一通り学習した後に取り組むと良いでしょう。
オススメその2
2冊目は『SPEED攻略10日間 数学 場合の数と確率』です。
Z会の教材は難しいというイメージがありますが、この教材は基本レベルから扱っているので、安心して取り組めます。
例題・類題・入試問題を繰り返し演習する構成になっており、典型問題の考え方や解き方を理解し、身につけることができます。
オススメその2
3冊目は『大学入試10日で極める 場合の数と確率』です。
どちらかと言えば、理系向けの教材です。短期間で、基礎から難関大突破レベルまで効率的に学習できます。
主要大学の入試において、近年出題率の高い分野の問題が掲載されているのもポイントです。また、補充問題も充実しているので、これ1冊で演習量もカバーできます。
さいごに、もう一度、頭の中を整理しよう
- 場合の数を調べるときは、樹形図を書く習慣を。
- 事柄の関係に応じて、和の法則や積の法則を使い分けよう。
- 樹が複数できたら、和の法則を利用しよう。
- 複数の樹の枝が同じ数であれば、積の法則を利用しよう。
- サイコロの問題では表も活用しよう。