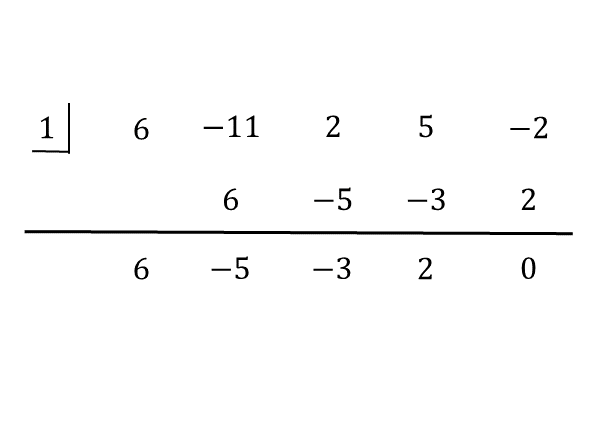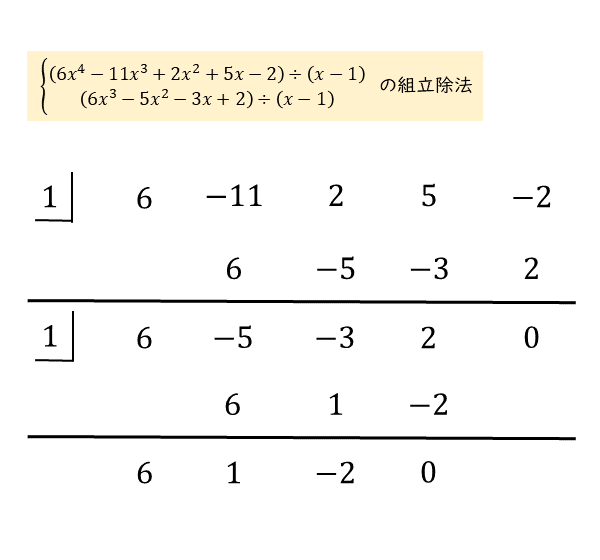数学２
今回は、高次方程式の解法について学習しましょう。高次方程式と言っても、高次式の扱いに従えば問題ありません。
前回とは異なる解法になります。入試ではこちらの解法の方をよく利用するので、しっかりマスターしましょう。
剰余の定理と因数定理
剰余の定理は、整式を１次式で割った余りを求めることができる定理です。
剰余の定理
\begin{align*}
&\text{1⃣ 整式 $P(x)$ を $1$ 次式 $x-k$ で割ったときの余りは} \\[ 5pt ]
&\quad P(k) \quad \text{（剰余の定理）} \\[ 10pt ]
&\text{2⃣ 整式 $P(x)$ を $1$ 次式 $ax+b$ で割ったときの余りは} \\[ 5pt ]
&\quad P \left(-\frac{b}{a} \right)
\end{align*}
剰余の定理を利用すれば、１次式で割った余りが分かりますが、ときには余りが０となることもあります。
このような場合、整式が１次式で割り切れるので、整式は割る式と商との積で表されます。つまり、割る１次式と商は、整式の因数となります。
これが因数定理です。因数定理は、剰余の定理において特に余りが０となるときの定理です。
因数定理
\begin{align*}
&\text{1⃣ $1$ 次式 $x-k$ が整式 $P(x)$ の因数である。} \\[ 5pt ]
&\quad \iff \ P(k)=0 \quad \text{（因数定理）} \\[ 10pt ]
&\text{2⃣ $1$ 次式 $ax+b$ が整式 $P(x)$ の因数である。} \\[ 5pt ]
&\quad \iff \ P \left(-\frac{b}{a} \right)=0
\end{align*}
剰余の定理を利用して、整式を１次式で割った余りを調べます。このとき、余りが０となれば、因数定理が成り立ちます。
因数定理が成り立てば、割る１次式は整式の因数と言えます。因数である１次式を用いると、整式を因数分解することができます。
因数定理を利用した高次方程式の解法
因数分解を利用した高次方程式の解法については、すでに学習済みです。ここでは、因数定理を利用した解法を学習します。
ほとんどの場合、因数定理を利用すれば、高次方程式を因数分解することができます。入試でも頻出なので、手順をしっかり把握しておきましょう。
因数定理を利用する解法では、方程式のｘに値を代入して、式の値を調べます。式の値によって、因数定理が成り立つかどうかが分かります。
ただし、自分で因数を探さなければならないので、要領が悪いといつまで経っても与式を因数分解できません。
因数定理が成り立つｘの値が分かれば、因数となる１次式が分かります。この１次式で整式を割って商を求めます。このときの割り算では、筆算でも良いですが、主に組立除法を利用します。
割る１次式が因数であれば、商も因数となるので、これらから整式を因数分解できます。あとは因数分解を利用した解法と同じ要領で方程式の解を求めます。
因数定理が成り立つ値を見つけるコツ
因数定理が成り立つｘの値を探すとき、小さな整数から順に代入していくのが基本的な取り組み方です。ただ、ある程度、予め候補を挙げておいて代入した方が効率的です。
候補を見つけるコツは、最高次の項の係数と定数項に注目することです。
Ｐ(ｋ)＝０となるｋの見つけ方
\begin{align*}
&\text{$P(k)=0$ となる $k$ の候補は} \\[ 5pt ]
&\quad \pm \frac{ \text{定数項の約数} }{ \text{最高次の係数の約数} }
\end{align*}
最高次の係数の約数と定数項の約数をそれぞれ調べ、それらをもとに候補を書き出します。
高次方程式を解いてみよう
因数定理を利用した高次方程式の解法を、例題を使って確認しましょう。
例題
\begin{align*}
&\text{次の方程式を解け。} \\[ 5pt ]
&(1) \quad x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6=0 \\[ 7pt ]
&(2) \quad 6x^{\scriptsize{4}}-11x^{\scriptsize{3}}+2x^{\scriptsize{2}}+5x-2=0
\end{align*}
例題(1)の解答・解説
例題(1)
\begin{align*}
&\text{次の方程式を解け。} \\[ 5pt ]
&\quad x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6=0
\end{align*}
与式は３次方程式です。左辺の３次式を見ると、残念ながら公式に当てはまる式ではありません。このような方程式では、因数定理を利用します。
与式の左辺を抜き出し、因数定理が成り立つ文字ｘの値を探します。すぐに見つからなくても、焦らないようにしましょう。候補を書き出して、順に代入していくと良いでしょう。
例題(1)の解答例 1⃣
\begin{align*}
&\quad x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6=0 \\[ 7pt ]
&\text{最高次の係数の約数 $\cdots \ 1$} \\[ 5pt ]
&\text{定数項の約数 $\cdots \ 1 \ , \ 2 \ , \ 3 \ , \ 6$} \\[ 5pt ]
&\text{よって、$x$ に代入する値の候補は} \\[ 5pt ]
&\quad \pm \frac{1}{1} \ , \ \pm \frac{2}{1} \ , \ \pm \frac{3}{1} \ , \ \pm \frac{6}{1} \\[ 7pt ]
&\text{すなわち} \\[ 5pt ]
&\quad \pm 1 \ , \ \pm 2 \ , \ \pm 3 \ , \ \pm 6 \\[ 7pt ]
&\text{よって、$-1$ や $1$ から代入していく。}
\end{align*}
代入する候補が分かりました。左辺の因数が１つでも分かれば良いので、計算しやすそうな数を選んで代入します。実際に答案にするのは解答例2⃣からです。
例題(1)の解答例 2⃣
\begin{align*}
&\quad x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6=0 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad \pm 1 \ , \ \pm 2 \ , \ \pm 3 \ , \ \pm 6 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad P(x)=x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6 \\[ 7pt ]
&\text{とすると、} \\[ 5pt ]
&\quad P(1)=1^{\scriptsize{3}}-7 \cdot 1^{\scriptsize{2}}+6=0 \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。}
\end{align*}
因数となる１次式が分かったら、組立除法で割り算します。因数で割り算するので、必ず割り切れます。組立除法の結果は以下の通りです。
例題(1)の組立除法 筆算よりも組立除法の方が楽に計算できます。
因数定理が成り立つときは、組立除法で割り算しよう。
３次式を１次式で割ると、商は２次式となります。組立除法の結果をもとに整式を因数分解します。
例題(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=x^{\scriptsize{3}}-7x^{\scriptsize{2}}+6 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。} \\[ 5pt ]
&\text{したがって} \\[ 5pt ]
&\quad P(x)=\left(x-1 \right)\left(x^{\scriptsize{2}}-6x-6 \right)
\end{align*}
ほとんどの場合、商は２次以上の整式となるので、因数分解できるかどうかを必ず確認しましょう。因数分解できないようなら先に進みます。
抜き出した整式は、もともと方程式の左辺にあったものです。整式を因数分解した後は、もとの方程式に戻ります。因数分解後の方程式を解いて解を求めます。
例題(1)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-1 \right)\left(x^{\scriptsize{2}}-6x-6 \right) \\[ 7pt ]
&\text{$P(x)=0$ であるので} \\[ 5pt ]
&\quad \left(x-1 \right)\left(x^{\scriptsize{2}}-6x-6 \right)=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad x-1=0 \ \text{または} \ x^{\scriptsize{2}}-6x-6=0 \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad x = 1 \ , \ 3 \pm \sqrt{15}
\end{align*}
新たに得られた２次方程式では、左辺を因数分解できません。解を求めるときは、解の公式を利用します。
補足
「$2$ 次方程式の左辺を因数分解できない」と説明したが、実際には異なる $2$ つの実数解をもつ。よって、複素数の範囲であれば
\begin{equation*}
\quad x^{\scriptsize{2}}-6x-6=\left(x-3 + \sqrt{15} \right)\left(x-3 – \sqrt{15} \right)
\end{equation*}
と因数分解できる。
ただ、解に平方根が含まれる場合、たすき掛けなどで因数分解できないので、わざわざ因数分解せずに、解の公式で直接解を求めるのが一般的である。
ここで「因数分解できない」とは、係数や定数項を整数で表せないという意味である。
２次方程式を解くとき、左辺を因数分解するのが難しいと感じたら、遠慮なく解の公式を利用しましょう。
例題(2)の解答・解説
例題(2)
\begin{align*}
&\text{次の方程式を解け。} \\[ 5pt ]
&\quad 6x^{\scriptsize{4}}-11x^{\scriptsize{3}}+2x^{\scriptsize{2}}+5x-2=0
\end{align*}
与式は４次方程式です。左辺が４次式なので、因数定理を利用して因数分解します。
与式の左辺を抜き出し、因数定理が成り立つｘの値を探します。候補を書き出して、順に代入していきましょう。
例題(2)の解答例 1⃣
\begin{align*}
&\quad 6x^{\scriptsize{4}}-11x^{\scriptsize{3}}+2x^{\scriptsize{2}}+5x-2=0 \\[ 7pt ]
&\quad P(x)=6x^{\scriptsize{4}}-11x^{\scriptsize{3}}+2x^{\scriptsize{2}}+5x-2 \\[ 7pt ]
&\text{とすると、} \\[ 5pt ]
&\quad P(1)=6 \cdot 1^{\scriptsize{4}}-11 \cdot 1^{\scriptsize{3}}+2 \cdot 1^{\scriptsize{2}}+5 \cdot 1-2=0 \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。}
\end{align*}
因数となる１次式が分かったので、組立除法で割り算します。因数で割り算するので、必ず割り切れて、余りが０になります。組立除法の結果は以下の通りです。
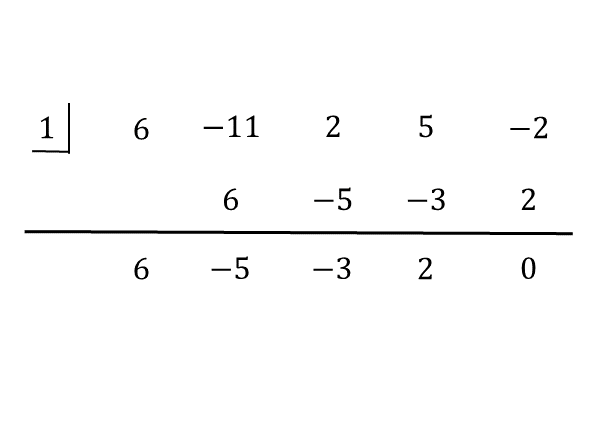例題(2)の組立除法 ４次式を１次式で割ると、商は３次式になります。組立除法の結果をもとに整式を因数分解します。
例題(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。} \\[ 5pt ]
&\text{したがって} \\[ 5pt ]
&\quad P(x)=\left(x-1 \right)\left(6x^{\scriptsize{3}}-5x^{\scriptsize{2}}-3x+2 \right)
\end{align*}
因数分解後の式において３次式だけを別途に抜き出します。因数定理を利用して、３次式を因数分解します。
例題(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-1 \right)\left(6x^{\scriptsize{3}}-5x^{\scriptsize{2}}-3x+2 \right) \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad Q(x)=6x^{\scriptsize{3}}-5x^{\scriptsize{2}}-3x+2 \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad Q(1)=6 \cdot 1^{\scriptsize{3}}-5 \cdot 1^{\scriptsize{2}}-3 \cdot 1+2=0 \\[ 7pt ]
&\text{より、$Q(x)$ は $x-1$ を因数にもつので} \\[ 5pt ]
&\quad Q(x)=\left(x-1 \right)\left(6x^{\scriptsize{2}}+x-2 \right)
\end{align*}
３次式の因数分解なので、因数が分かったら、組立除法で割り算した結果を利用します。
２度目の組立除法の結果は以下の通りです。２度目の組立除法は１度目の結果の下に続けて記述します。
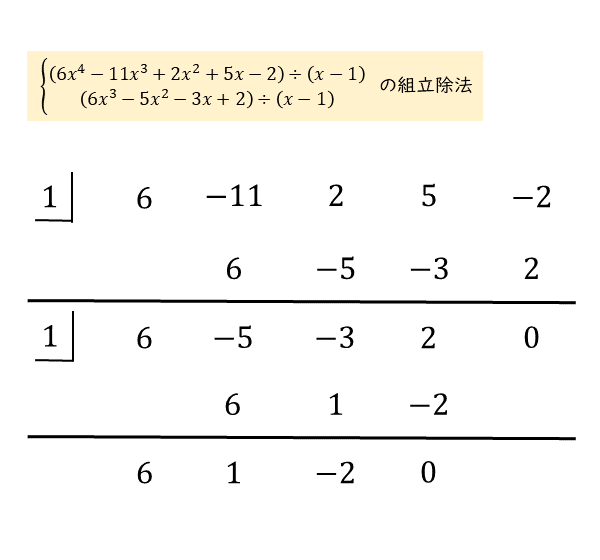例題(2)の組立除法のつづき 因数分解した後も２次式が残るので、たすき掛けでさらに因数分解します。
例題(2)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-1 \right)\left(6x^{\scriptsize{3}}-5x^{\scriptsize{2}}-3x+2 \right) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad Q(x)=\left(x-1 \right)\left(6x^{\scriptsize{2}}+x-2 \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad Q(x)=\left(x-1 \right)\left(2x-1 \right)\left(3x+2 \right) \\[ 7pt ]
&\text{これより} \\[ 5pt ]
&\quad P(x)=\left(x-1 \right)^{\scriptsize{2}}\left(2x-1 \right)\left(3x+2 \right)
\end{align*}
抜き出した整式は、もともと方程式の左辺にあったものです。整式を因数分解した後は、もとの方程式に戻ります。因数分解後の方程式を解いて解を求めます。
例題(2)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-1 \right)^{\scriptsize{2}}\left(2x-1 \right)\left(3x+2 \right) \\[ 7pt ]
&\text{$P(x)=0$ であるので} \\[ 5pt ]
&\quad x-1=0 \ \text{または} \ 2x-1=0 \ \text{または} \ 3x+2=0 \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad x = 1 \ \text{（重解）} \ , \ \frac{1}{2} \ , \ -\frac{2}{3}
\end{align*}
因数分解した結果を見ると、整式が同じ因数を２つもつことが分かります。このことから、４次方程式は２重解（ｘ＝１）を解にもつことが分かります。
因数定理を利用した解法では、いかに効率よく因数を見つけるかがポイントです。割り算には組立除法を利用できるので、それほど大変ではありません。
また、因数分解した後は、因数分解を利用した解法と同じ要領で解けます。因数分解までの過程が方程式によって異なるだけです。
因数定理を利用した高次方程式の解法の手順をまとめると、以下のようになります。
因数定理を利用した高次方程式の解法
- 方程式の左辺にある整式を抜き出す。
- 抜き出した整式において、因数定理が成り立つｘの値を探す。
- 因数定理が成り立つｘの値から、因数となる１次式が分かる。
- 因数の１次式で整式を割る（組立除法）。
- 商が分ったら整式を因数分解する。
- 因数がすべて２次式以下になったら、もとの方程式に戻る。
- 因数分解後の方程式を解いて、解を求める。
高次の整式によっては、割り算したときの商が３次以上の高次式になることがあります。
このような場合、商だけを抜き出し、その因数を見つけて組立除法により因数分解します。因数をさらに見つける必要があるかどうかは、商が２次以下の整式であることが目安になります。
次は、高次方程式の解法（因数定理の利用）を扱った問題を実際に解いてみましょう。
