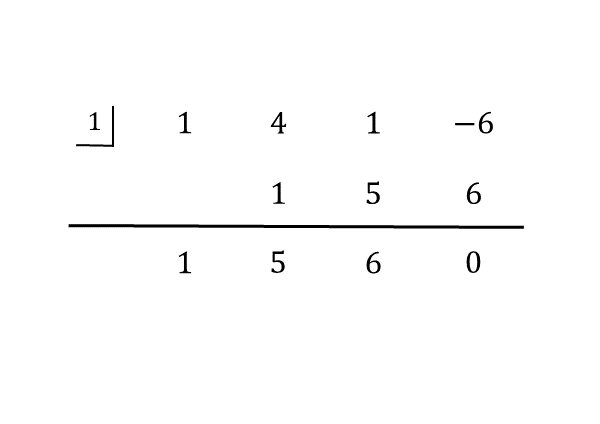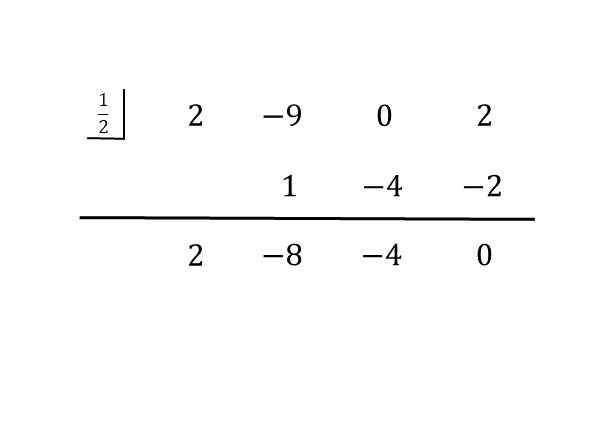数学２
高次式の因数分解を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*}
&\text{次の式を因数分解せよ} \\[ 5pt ]
&(1) \quad x^{\scriptsize{3}}+4x^{\scriptsize{2}}+x-6 \\[ 7pt ]
&(2) \quad 2x^{\scriptsize{3}}-9x^{\scriptsize{2}}+2
\end{align*}
問(1)の解答・解説
問(1)
\begin{align*}
&\text{次の式を因数分解せよ} \\[ 5pt ]
&\quad x^{\scriptsize{3}}+4x^{\scriptsize{2}}+x-6
\end{align*}
与式の３次式は、展開や因数分解の公式に当てはまる式ではありません。ですから、与式の因数となる１次式を見つけます。剰余の定理を利用して、余りが０となるｘの値を見つけます。
問(1)の解答例 1⃣
\begin{align*}
&\quad P(x)=x^{\scriptsize{3}}+4x^{\scriptsize{2}}+x-6 \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad P(1)=1^{\scriptsize{3}}+4 \cdot 1^{\scriptsize{2}}+1-6=0 \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。}
\end{align*}
ｘ＝１のとき式の値が０となるので、剰余の定理から与式を１次式ｘ－１で割った余りが０になります。このとき、因数定理が成り立つので、１次式ｘ－１は与式の因数になります。
因数である１次式が分かったので、組立除法で割り算して商を調べます。組立除法で割り算すると以下のようになります。
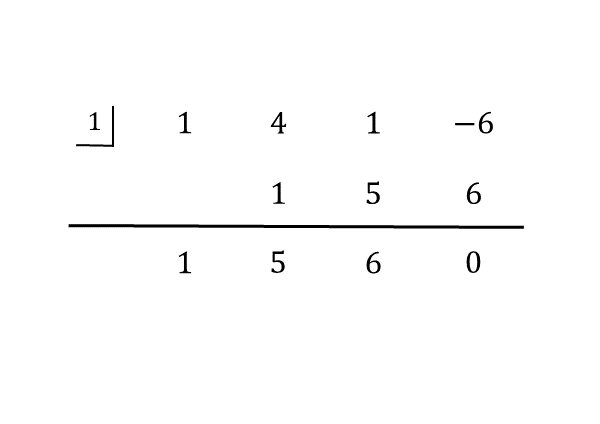問(1)の組立除法 組立除法を用いると、与式が３次式なので、２次式の商が得られます。因数定理が成り立つので、余りが０になっていることも分かります。
組立除法の結果から、与えられた整式は、割る１次式と商の積で表されます。
問(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{よって、$P(x)$ は $x-1$ を因数にもつ。} \\[ 5pt ]
&\text{$P(x)$ を因数分解すると} \\[ 5pt ]
&\quad P(x)=\left(x-1 \right) \left(x^{\scriptsize{2}}+5x+6 \right)
\end{align*}
商も与式の因数です。商は２次式であるので、もしかすると因数分解できるかもしれません。因数分解できれば、忘れずに因数分解します。
問(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-1 \right) \left(x^{\scriptsize{2}}+5x+6 \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad P(x)=\left(x-1 \right) \left(x+2 \right) \left(x+3 \right) \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad x^{\scriptsize{3}}+4x^{\scriptsize{2}}+x-6=\left(x-1 \right) \left(x+2 \right) \left(x+3 \right)
\end{align*}
２次式以上の整式があれば、因数分解できるかどうかを必ず調べましょう。
問(2)の解答・解説
問(2)
\begin{align*}
&\text{次の式を因数分解せよ} \\[ 5pt ]
&\quad 2x^{\scriptsize{3}}-9x^{\scriptsize{2}}+2
\end{align*}
与式の因数となる１次式を見つけます。剰余の定理を利用して、余りが０となるｘの値を見つけます。
問(2)の解答例 1⃣
\begin{align*}
&\quad P(x)=2x^{\scriptsize{3}}-9x^{\scriptsize{2}}+2 \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad P\left(\frac{1}{2} \right)=2 \cdot \left(\frac{1}{2} \right)^{\scriptsize{3}}-9 \cdot \left(\frac{1}{2} \right)^{\scriptsize{2}}+2=0 \\[ 7pt ]
&\text{よって、$P(x)$ は $x-\frac{1}{2}$ を因数にもつ。}
\end{align*}
ｘ＝１/２のとき式の値が０となるので、剰余の定理から与式を１次式ｘ－１/２で割った余りが０になります。このとき、因数定理が成り立つので、１次式ｘ－１/２は与式の因数になります。
因数である１次式が分かったので、組立除法で割り算して商を調べます。組立除法で割り算すると以下のようになります。ただし、割られる整式には１次の項がないので、その係数は０とします。
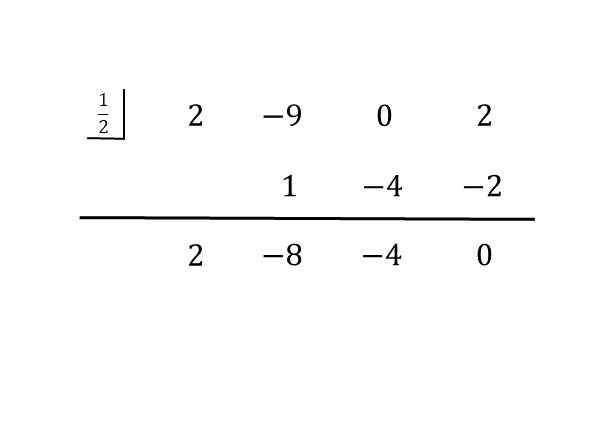問(2)の組立除法 組立除法を用いると、与式が３次式なので、２次式の商が得られます。因数定理が成り立つので、余りが０になっていることも分かります。
組立除法の結果から、与えられた整式は、割る１次式と商の積で表されます。
問(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{よって、$P(x)$ は $x-\frac{1}{2}$ を因数にもつ。} \\[ 5pt ]
&\text{$P(x)$ を因数分解すると} \\[ 5pt ]
&\quad P(x)=\left(x-\frac{1}{2} \right) \left(2x^{\scriptsize{2}}-8x-4 \right)
\end{align*}
商も与式の因数です。商は２次式であるので、もしかすると因数分解できるかもしれません。因数分解できるかを必ず確認しましょう。
問(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P(x)=\left(x-\frac{1}{2} \right) \left(2x^{\scriptsize{2}}-8x-4 \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad P(x)=\left(x-\frac{1}{2} \right) \cdot 2\left(x^{\scriptsize{2}}-4x-2 \right) \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad P(x)=\left(2x-1 \bigr) \bigl(x^{\scriptsize{2}}-4x-2 \right) \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad 2x^{\scriptsize{3}}-9x^{\scriptsize{2}}+2=\left(2x-1 \bigr) \bigl(x^{\scriptsize{2}}-4x-2 \right)
\end{align*}
組立除法では、割る１次式の係数は１です。ですから、因数を考えるとき、割る１次式を２ｘ－１としないように気を付けましょう。
また、有理数の範囲では、商の２次式から共通因数でくくること以外に因数分解できません。
組立除法を用いる解法では、割る１次式の係数は１であることに注意しよう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学２・Ｂや数学３では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 剰余の定理は、整式を１次式で割ったときの余りについての定理。
- 余りが０となるとき、割る１次式は整式の因数（因数定理）。
- 整式の因数の１つが分かれば、その他の因数も分かる。
- 割る式が１次式のとき、組立除法で商と余りを調べることができる。
- 組立除法では、割る１次式の係数は１であることに注意。
