式と証明｜３次式の因数分解について

08/23/2022数学２

今回は、３次式の因数分解について学習しましょう。

因数分解の単元で躓くのは、展開の公式を覚えていないことが原因です。これは２次式でも３次式でも同じです。

覚えていない人は展開の公式を見ながらで良いので、使いながら覚えましょう。

1. 式の因数分解について
2. ３次式の因数分解の公式
3. 因数分解の手順
4. ３次式の因数分解を扱った問題を解いてみよう
5. Recommended books
- 5.1. オススメその１『合格る計算数学１・A・２・Ｂ』
- 5.2. オススメその２『鉄緑会基礎力完成数学Ⅰ・Ａ＋Ⅱ・Ｂ』
6. さいごにもう一度まとめ

式の因数分解について

式の因数分解は、与式を単項式や多項式の積の形で表すことです。単項式の和の形（＝多項式）で表す展開とは逆の操作が因数分解です。

一般に、展開よりも因数分解の方が難しく感じるでしょう。

展開の場合、公式があるとは言っても、本質的には分配法則による変形です。ですから、最悪、公式を覚えていなくても分配法則さえできれば展開することはできます。

それに対して因数分解の場合、分配法則の逆の操作をすれば良いのですが、これが意外と難しいのです。

たとえば、以下の式を因数分解する場合を考えてみましょう。

共通因数が見当たらない式の例

$\begin{align*} &\quad a^{3} +b^{3} \\[ 7pt ] &\quad a^{3} -b^{3} \end{align*}$

一般に、分配法則によって展開された整式には、共通因数が存在します。

しかし、例に挙げた３次式には共通因数が見当たりません。このような場合、分配法則の逆の操作を行うことができません。

これらの式を導出したときを思い出すと理由が分かります。

分配法則の逆ができないのは、同類項が原因です。同類項の計算によって、４つの項が消えてしまったからです。

共通因数が見当たらないのは同類項が原因

$\begin{align*} \quad &\left(a+b \right)\left(a^{2}-ab+b^{2} \right) \\[ 7pt ] &= \ a\left(a^{2}-ab+b^{2} \right)+b\left(a^{2}-ab+b^{2} \right) \\[ 7pt ] &= \ a^{3}\underline{-a^{2}b} \ \underline{\underline{+ab^{2}}} \ \underline{+a^{2}b} \ \underline{\underline{-ab^{2}}}+b^{3} \\[ 7pt ] &= \ a^{3} +b^{3} \end{align*}$

このように共通因数が見当たらない場合、式を因数分解するには公式に頼らなければなりません。きちんと覚えておく方が無難でしょう。

式と証明｜３次式の展開について

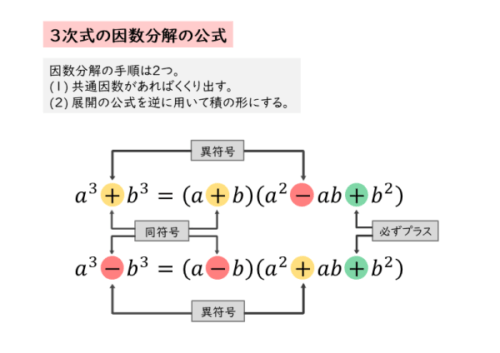
３次式の因数分解の公式

３次式の因数分解では、覚えておく公式は２つです。

３次式の因数分解の公式

$\begin{align*} &\quad a^{3} +b^{3} = \left(a + b \right)\left(a^{2} -ab +b^{2} \right) \quad \cdots \text{①} \\[ 7pt ] &\quad a^{3} -b^{3} = \left(a – b \right)\left(a^{2} +ab +b^{2} \right) \quad \cdots \text{②} \end{align*}$

展開の公式において、左辺と右辺を逆にしただけです。

特に間違えやすいのは符号なので、符号に注目するとミスを減らせるでしょう。

共通点や相違点を意識しながら覚えましょう。

因数分解の手順

因数分解では、一応、決まった手順があります。そのためには、展開のことを知っておかなければなりません。

上述したように、展開は本質的には分配法則による変形です。その中でも、同類項の整理によって項の数が変わったものに対しては、展開の公式として公式化されています。

このことを踏まえると、展開のパターンは以下の２通りです。

展開のパターン

分配法則を用いて展開する（展開後にすべての項が残っている）
公式を用いて展開する（展開後に同類項が整理されてなくなる）

このように展開には２つのパターンがあるので、パターンに応じた因数分解を行う必要があります。

因数分解のパターン

分配法則を逆に用いて因数分解する（各項に共通のもの（＝共通因数）をくくり出す）
展開の公式を逆に用いて因数分解する（与式の形から判断）

因数分解にもパターンがあることが分かりましたが、具体的な手順は以下のようになります。

因数分解の手順

分配法則を逆に用いて、共通因数をくくり出す
展開の公式を逆に用いる

優先順位が高いのは、共通因数をくくり出すことです。もし、共通因数がなければ、公式に当てはまっていないかを考えます。

応用的な問題になると、２つのパターンが混在しています。優先順位を守って因数分解することが大切です。

整式の因数分解では、共通因数でくくることが最優先。

次は、３次式の因数分解を扱った問題を実際に解いてみましょう。

３次式の因数分解を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

次の式を因数分解せよ。

$\begin{align*} &(1) \quad cx^{3} -8c \\[ 7pt ] &(2) \quad a^{3} +27b^{3} \\[ 7pt ] &(3) \quad x^{3} -3x^{3} +3x -1 \end{align*}$

最初のうちは公式を見ながらで良いので、対応関係を考えながら公式を使ってみましょう。

問(1)の解答・解説

問(1)

次の式を因数分解せよ。

$\begin{align*} \quad cx^{3} -8c \end{align*}$

問(1)の与式は、２項からなる式ですが、各項に共通の文字ｃがあります。この文字ｃを共通因数と言います。

分配法則を逆に行い、共通因数をくくり出します。

問(1)の解答例 1⃣

$\begin{align*} \quad cx^{3} -8c = c\left(x^{3} -8 \right) \end{align*}$

共通因数をくくり出せました。しかし、ここで終わってはいけません。

次に、カッコ内の３次式に注目します。３次式なので、因数分解できる可能性が高いです。

２次以上の式が残っていれば、まだ因数分解できるかもと考えよう。

因数分解の公式②に当てはまります。公式との対応関係を調べます。

公式との対応関係を調べる

$\begin{align*} &\quad \underline{a^{3} -b^{3}} = \left(a – b \right) \left(a^{2} +ab +b^{2} \right) \quad \cdots \text{②} \\[ 10pt ] &\quad c(x^{3} -8) = c \left(\underline{x^{3} -2^{3}} \right) \end{align*}$

下線を引いた $2$ つの式を比べると

$\begin{align*} \quad a=x \ , \ b=2 \end{align*}$

の対応関係がある。

公式との対応関係が分かったので、対応するものに置き換えていきます。置き換えたら、各項をそれぞれ整理します。

問(1)の解答例 2⃣

$\begin{align*} \quad cx^{3} -8c &= c\left(x^{3} -8 \right) \\[ 7pt ] &= \ c\left(x^{3} -2^{3} \right) \\[ 7pt ] &= \ c\left(x-2 \right)\left(x^{2} +x \cdot 2 +2^{2} \right) \\[ 7pt ] &= \ c\left(x-2 \right)\left(x^{2} +2x +4 \right) \end{align*}$

$\begin{align*} \therefore \ cx^{3} -8c = c\left(x-2 \right)\left(x^{2} +2x +4 \right) \end{align*}$

公式を利用する場合、その都度、確認しながら覚えましょう。

３次式の因数分解の公式

問(2)の解答・解説

問(2)

次の式を因数分解せよ。

$\begin{align*} \quad a^{3} +27b^{3} \end{align*}$

問(2)は、因数分解の公式①に当てはまります。利用できる公式を探すコツは、係数よりも文字や次数に注目することです。

公式との対応関係を調べます。

公式との対応関係を調べる

$\begin{align*} &\quad \underline{a^{3} +b^{3}} = \left(a + b \right) \left(a^{2} -ab +b^{2} \right) \quad \cdots \text{①} \\[ 10pt ] &\quad a^{3} +27b^{3} = \underline{a^{3} + \left(3b \right)^{3}} \end{align*}$

下線を引いた $2$ つの式を比べると

$\begin{align*} \quad a=a \ , \ b=3b \end{align*}$

の対応関係がある。

公式との対応関係が分かったので、対応するものに置き換えていきます。置き換えたら、各項をそれぞれ整理します。

問(2)の解答例

$\begin{align*} \quad a^{3} +27b^{3} &= a^{3} + \left(3b \right)^{3} \\[ 7pt ] &= \ \left(a + 3b \right) \left\{ a^{2} -a \cdot 3b +\left(3b \right)^{2} \right\} \\[ 7pt ] &= \ \left(a + 3b \right) \left(a^{2} -3ab +9b^{2} \right) \end{align*}$

$\begin{align*} \therefore \ a^{3} +27b^{3} = \left(a + 3b \right) \left(a^{2} -3ab +9b^{2} \right) \end{align*}$

よく間違えるのが、係数の扱いです。問(2)では、ｂを３ｂに置き換えるので、間違いやすくなります。

また、係数を２乗したり、３乗したりするのを忘れやすいので気をつけましょう。

問(3)の解答・解説

問(3)

次の式を因数分解せよ。

$\begin{align*} \quad x^{3} -3x^{2} +3x -1 \end{align*}$

問(3)は、３次式の乗法公式の②式に当てはまります。この公式を逆に用いて因数分解します。

３次式の乗法公式その１

$\begin{align*} &\quad \left(a + b \right)^{3} = a^{3} +3a^{2}b +3ab^{2} +b^{3} \quad \cdots \text{①} \\[ 7pt ] &\quad \left(a – b \right)^{3} = a^{3} -3a^{2}b +3ab^{2} -b^{3} \quad \cdots \text{②} \end{align*}$

公式との対応関係を調べます。

公式との対応関係を調べる

$\begin{align*} &\quad \left(a – b \right)^{3} = \underline{a^{3} -3a^{2}b +3ab^{2} -b^{3}} \quad \cdots \text{②} \\[ 10pt ] &\quad x^{3} -3x^{2} +3x -1 = \underline{x^{3} -3x^{2} \cdot 1 +3x \cdot 1^{2} -1^{3}} \end{align*}$

下線を引いた $2$ つの式を比べると