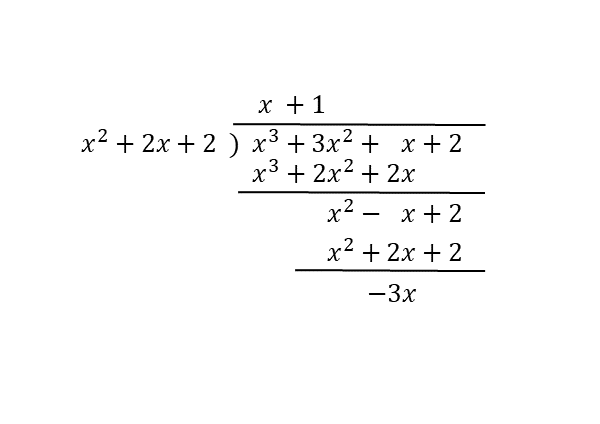複素数と方程式｜高次式の値について

数学２

今回は、高次式の値について学習しましょう。式の値を求める問題は、ほとんどの単元で扱われます。

高次式の値を求める場合、これまでの基本的な求め方のほかに、高次式ならではの考え方を用いて求めます。求め方はもちろんですが、高次式を扱うときの考え方をしっかりマスターしましょう。

高次式の値

式の値を求める場合、一般に式に数を代入して計算します。これが基本的な解法です。

しかし、高次式のように次数の高い整式となると、累乗の計算が増え、代入する箇所も増えます。

特に、項の多い高次式の場合、代入するものが複素数であることがほとんどです。そうなると、計算が非常に煩雑になります。

高次式の値を求めるときに意識したいのは、次数を下げることです。

次数を下げることによって、計算をできるだけ簡単にすることができます。また、代入する箇所も少なくなるので、やはり計算ミスを減らすことができます。

高次式の値を求めるとき、高次式の次数を下げよう。

次数を下げる方法

高次式の次数を下げるには、割り算を利用します。つまり、割り算の基本公式を利用して、高次式を割る式や商、そして余りの３つに分解してしまうのです。

関連記事

式と証明｜整式の割り算について

割る式や商、そして余りは、もとの高次式よりも次数が低い式です。次数が低くなれば、高次式に比べて式の値を計算しやすくなります。

問題は「割る式をどのようにして手に入れるか」です。手に入れるというよりも、作ると言った方が適切ですが、この手順を覚えることはさほど難しくありません。ただし、理解するためには２次方程式とその解についての知識が必要です。

高次式を割り算して次数を下げよう。

概要が分かったところで、高次式の値の求め方を例題で確認しましょう。

高次式の値を求めてみよう

次の例題を考えてみましょう。

例題

\begin{align*} &\text{$x=-1+i$ のとき、$P=x^{\scriptsize{3}}+3x^{\scriptsize{2}}+x+2$ の値を求めたい。} \\[ 5pt ] &(1) \quad \text{$x^{\scriptsize{2}}+2x+2=0$ であることを証明せよ。} \\[ 7pt ] &(2) \quad \text{$P$ を $x^{\scriptsize{2}}+2x+2$ 割った商と余りを求めよ。} \\[ 7pt ] &(3) \quad \text{$P$ の値を求めよ。} \end{align*}

最終目標は、(3)の高次式の値を求めることです。つまり、最終目標である(3)を解くためには、(1)，(2)の結果が必要ということです。

例題(1)の解答・解説

例題(1)

\begin{align*} &\text{$x=-1+i$ のとき、$P=x^{\scriptsize{3}}+3x^{\scriptsize{2}}+x+2$ の値を求めたい。} \\[ 5pt ] &\text{$x^{\scriptsize{2}}+2x+2=0$ であることを証明せよ。} \end{align*}

例題(1)は、等式が成り立つことを証明する問題です。最も簡単な考え方は、左辺の２次式の値を求めることです。

与えられたｘの値を左辺の２次式に代入します。

例題(1)の解答例

\begin{align*} &\text{$x=-1+i$ のとき} \\[ 5pt ] &\qquad x^{\scriptsize{2}}+2x+2 \\[ 7pt ] &\quad =\left(-1+i \right)^{\scriptsize{2}}+2\left(-1+i \right)+2 \\[ 7pt ] &\quad =1-2i+i^{\scriptsize{2}}-2+2i+2 \\[ 7pt ] &\quad =1-1 \\[ 7pt ] &\quad =0 \\[ 7pt ] &\text{よって、$x=-1+i$ のとき} \\[ 5pt ] &\quad x^{\scriptsize{2}}+2x+2=0 \end{align*}

ｘ＝－１＋ｉのとき、等式が成り立つことが示せました。(1)の２次式は、ｘについての２次方程式と捉えることができます。このことから、ｘ＝－１＋ｉは２次方程式の解であると言えます。

式の値を求める問題では、上述した解答例が最も直接的な解法です。しかし、複素数を代入するので計算が少し面倒です。

特に、虚数単位の取り扱いでミスをしがちです。ですから、以下のような解法もあります。

例題(1)の別解例その１

\begin{align*} &\text{$x=-1+i$ より} \\[ 5pt ] &\quad x+1=i \\[ 7pt ] &\text{両辺を $2$ 乗すると} \\[ 5pt ] &\quad \left(x+1 \right)^{\scriptsize{2}}=-1 \\[ 7pt ] &\text{これを整理すると} \\[ 5pt ] &\quad x^{\scriptsize{2}}+2x+2=0 \end{align*}

虚数単位が消えるように複素数を変形すると、この複素数を解にもつ２次方程式を作ることができます。

このことは、解の公式を導出した経験があれば理解できます。解の公式の導出手順を逆にたどっています。つまり、解から逆算して、もとの２次方程式を作るのが別解の考え方です。

この解法の最大の利点は、虚数単位の扱いにほとんど気を遣う必要がないことです。別解として挙げましたが、模範解答として紹介されることもある解法です。

与えられた解が複素数であれば、複素数から２次方程式を作ろう。

なお、他の別解例としては、共役な複素数を考えて、解と係数の関係から２次方程式を求める解法もあります。

例題(1)の別解例その２

\begin{align*} &\text{$x=-1+i$ を解にもつ $2$ 次方程式は、} \\[ 5pt ] &\text{共役な複素数 $-1-i$ も解にもつ。} \\[ 5pt ] &\text{このとき} \\[ 5pt ] &\quad \left(-1+i \right)+\left(-1-i \right)=-2 \\[ 7pt ] &\quad \left(-1+i \right) \left(-1-i \right)=2 \\[ 7pt ] &\text{より、$x=-1+i$ を解にもつ $2$ 次方程式は} \\[ 5pt ] &\quad x^{\scriptsize{2}}+2x+2=0 \end{align*}

なお、２次方程式が複素数を解にもつとき、共役な複素数も解にもつことを利用しています。２つの解が分かれば、２つの解の和と積を求めて２次方程式の係数を決めることができます。

関連記事

複素数と方程式｜２つの数を解とする２次方程式の作成について

例題(2)の解答・解説

例題(2)

\begin{align*} &\text{$x=-1+i$ のとき、$P=x^{\scriptsize{3}}+3x^{\scriptsize{2}}+x+2$ の値を求めたい。} \\[ 5pt ] &\text{$P$ を $x^{\scriptsize{2}}+2x+2$ 割った商と余りを求めよ。} \end{align*}

３次式である与式を例題(1)で得た２次式で割ります。注意したいのは、組立除法を利用できないことです。組立除法を利用できるのは、割る式が１次式のときです。

３次式を２次式で割り算します。丁寧に筆算しましょう。

高次式の割り算(1)
３次式を２次式で割る

割られる式の次数の高い項から順に消去していきます。余りが割る式の次数よりも低くなれば、割り算を終えます。

割る式が２次式なので、余りは１次式または定数です。割り算の結果を利用して答案を作成します。筆算も消さずに答案に残しておきましょう。

例題(2)の解答例

\begin{align*} &\text{筆算の結果から} \\[ 5pt ] &\quad \text{商} \quad x+1 \\[ 7pt ] &\quad \text{余り} \quad -3x \end{align*}

これでようやく例題(3)を解く準備が整いました。

例題(3)の解答・解説

例題(3)

\begin{align*} &\text{$x=-1+i$ のとき、$P=x^{\scriptsize{3}}+3x^{\scriptsize{2}}+x+2$ の値を求めたい。} \\[ 5pt ] &\text{$P$ の値を求めよ。} \end{align*}

(1)，(2)の結果を上手に利用します。与式Ｐを(1)の２次式で割ったときの商と余りを(2)で求めました。これらを用いて与式Ｐを表します。

例題(3)の解答例 1⃣

\begin{align*} &\text{$(2)$ より} \\[ 5pt ] &\quad P=\left(x^{\scriptsize{2}}+2x+2 \right) \left(x+1 \right)-3x \end{align*}

割り算の基本公式を利用して、３次式を２次式や１次式で表すことができました。その結果、多項式にはなりましたが、次数が下がりました。

ｘ＝－１＋ｉのときの与式Ｐの値を求めるために、(1)の結果を利用します。

例題(3)の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad P=\left(x^{\scriptsize{2}}+2x+2 \right) \left(x+1 \right)-3x \\[ 7pt ] &\text{さらに $(1)$ と $x=-1+i$ より} \\[ 5pt ] &\quad P=0 \cdot \left(-1+i+1 \right)-3\left(-1+i \right) \\[ 7pt ] &\text{すなわち} \\[ 5pt ] &\quad P=3-3i \end{align*}

(1)の結果を利用できるのは、ｘ＝－１＋ｉのときです。ですから、(1)の結果を利用するときに合わせて、与えられた複素数を代入しましょう。

ｘ＝－１＋ｉは(1)の２次方程式の解でした。ですから、方程式に代入すると等式が成り立つので、左辺の２次式の値は０になります。この２次式は割る式なので、ｘ＝－１＋ｉを代入すると割る式の値は０になります。

その結果、実際に計算するのは余りの部分だけになります。虚数単位の扱いでミスをすることはほとんどないでしょう。

入試などでは、(3)だけが単独で出題されることが多いのがこの問題の特徴です。そういう場合であっても、(1)，(2)の作業が必要になります。

遠回りと感じるかもしれませんが、与式を変形せずに代入することに比べれば、計算の負担ははるかに少なくなります。

また、次数を下げるという考え方を身に付けるという点でも大切な解法です。なお、この考え方は他の単元でも扱われるので覚えておきましょう。

問題を解決する手段はいくつあっても良いものです。複数の視点をもつことにもなるので、引き出しを増やしましょう。

次は、高次式の値を扱った問題を実際に解いてみましょう。

数学２次数,割り算,複素数と方程式,高次式

Posted by kiri