図形の性質｜円に内接する四角形について

10/17/2021数学Ａ

今回は円に内接する四角形について学習しましょう。円に内接する図形では三角形を扱う方が多いですが、高校では四角形も扱うようになります。

また、この単元では証明問題もよく出題されるので、積極的に取り組んで記述の能力を向上させましょう。

記事の画像が見辛いときはクリックすると拡大できます。

円に内接する四角形

円に内接する四角形は、いくつか性質をもちます。

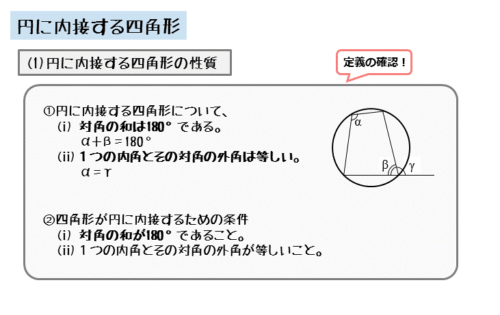
円に内接する四角形の性質

対角の和は１８０°である。
１つの内角とその対角の外角は等しい。

また、四角形が円に内接するためには、いくつか条件があります。どちらかを満たせば、四角形は円に内接します。

四角形が円に内接するための条件

対角の和が１８０°であること。
１つの内角とその対角の外角が等しいこと。

証明問題では、主に四角形が円に内接していることを証明します。このとき、四角形が円に内接するための条件を満たしていることを示します。

また、円周角の定理の逆を利用することもあるので、これまでに学習した内容もしっかりと復習しておくことが大切です。

次は円に内接する四角形の性質を導出してみましょう。

円に内接する四角形の性質を導出しよう

円に内接する四角形の性質を実際に導出してみましょう。自力で導出できるか、力試しにチャレンジしてみましょう。

対角の和は１８０°であることの証明

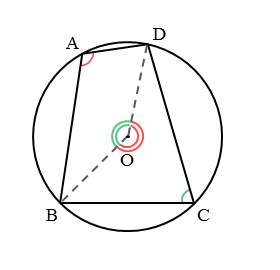
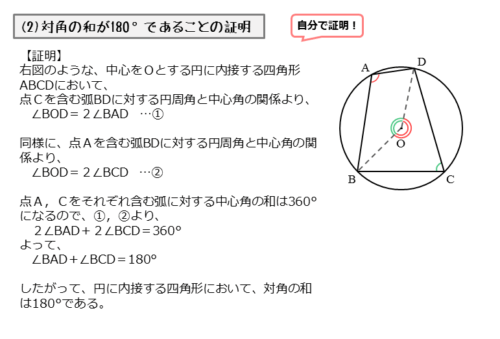
図のような点Ｏを中心とする円に内接する四角形ＡＢＣＤがあるとします。

点Ｃを含む弧ＢＤにおいて、∠ＢＡＤと∠ＢＯＤは１つの弧に対してできた円周角と中心角です。これより、円周角の定理が成り立つので、以下のように表せます。

点Ｃを含む弧ＢＤに対する∠ＢＡＤと∠ＢＯＤの関係

点 $C$ を含む弧 $BD$ において、円周角の定理より

\begin{align*} \quad \angle BOD = 2 \angle BAD \quad \cdots \text{①} \end{align*}

また、点Ａを含む弧ＢＤにおいても円周角の定理が成り立つので、以下のように表せます。

点Ａを含む弧ＢＤに対する∠ＢＣＤと∠ＢＯＤの関係

点 $A$ を含む弧 $BD$ において、円周角の定理より

\begin{align*} \quad \angle BOD = 2 \angle BCD \quad \cdots \text{②} \end{align*}

２つの中心角∠ＢＯＤの和が３６０°になることを利用します。①，②式から、四角形の対角の関係を導くことができます。

∠ＢＡＤと∠ＢＣＤの関係

\begin{align*} &\vdots \\[ 7pt ] \quad \angle BOD &= 2 \angle BAD \quad \cdots \text{①} \\[ 7pt ] &\vdots \\[ 7pt ] \quad \angle BOD &= 2 \angle BCD \quad \cdots \text{②} \end{align*}

①，②より

\begin{align*} \quad 2 \angle BAD + 2 \angle BCD = 360^{\circ} \end{align*}

よって

\begin{align*} \quad \angle BAD + \angle BCD = 180^{\circ} \quad \cdots \text{③} \end{align*}

四角形の対角である∠ＢＡＤと∠ＢＣＤの関係は、③式のように表せます。これより、円に内接する四角形の対角の和が１８０°であることを示すことができました。

１つの内角とその対角の外角は等しいことの証明

１つの内角とその対角の外角は等しいことの証明は、円に内接する四角形の対角の和が１８０°であることを利用します。

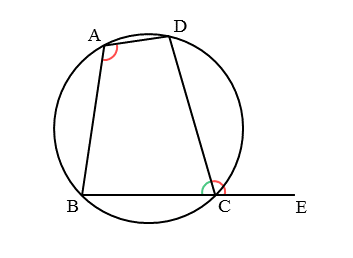
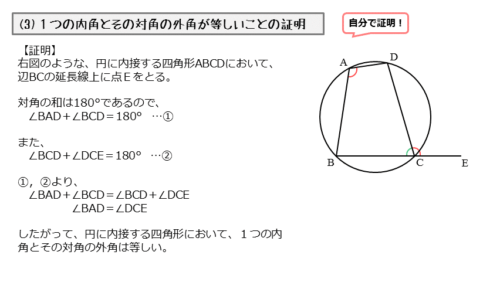
図のように、四角形ＡＢＣＤが円に内接するとき、辺ＢＣの延長線上に点Ｅをとります。このとき、円に内接する四角形の対角の和を利用します。

円に内接する四角形の対角の和を利用

四角形 $ABCD$ は円に内接するので

\begin{align*} \quad \angle BAD + \angle BCD = 180^{\circ} \quad \cdots \text{①} \end{align*}

1つの内角はその対角の外角に等しいことを証明する図 — 円に内接する四角形ＡＢＣＤ

次に、∠ＤＣＥが∠ＢＣＤの外角であることを利用します。

内角とその外角の関係を利用

また、四角形の内角とその外角の関係から

\begin{align*} \quad \angle BCD + \angle DCE = 180^{\circ} \quad \cdots \text{②} \end{align*}

①，②式から、∠ＢＡＤと∠ＢＣＤの関係を導きます。

∠ＢＡＤと∠ＢＣＤの関係

\begin{align*} &\vdots \\[ 7pt ] \quad \angle BAD &+ \angle BCD = 180^{\circ} \quad \cdots \text{①} \\[ 7pt ] &\vdots \\[ 7pt ] \quad \angle BCD &+ \angle DCE = 180^{\circ} \quad \cdots \text{②} \end{align*}

①，②より

\begin{align*} \quad \angle BAD + \angle BCD = \angle BCD + \angle DCE \end{align*}

よって

\begin{align*} \quad \angle BAD = \angle BCD \quad \cdots \text{③} \end{align*}

∠ＢＡＤは円に内接する四角形の１つの内角です。また、∠ＢＣＤは∠ＢＡＤの対角の外角です。

∠ＢＡＤと∠ＤＣＥの関係は、③式のように表せます。これより、１つの内角とその対角の外角が等しいことを示すことができました。