図形と方程式｜三角形の面積について

01/26/2023数学２

三角形の面積を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

次の $3$ 点

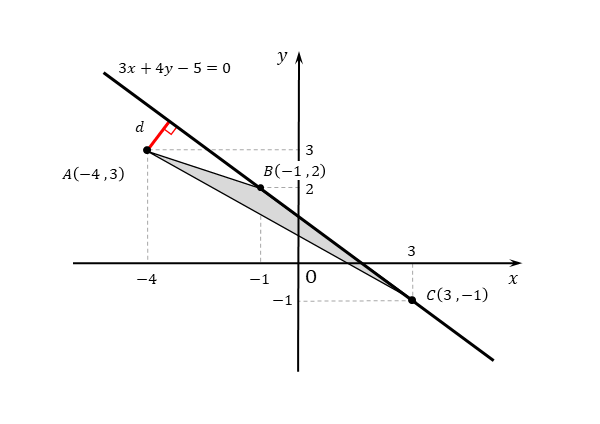
$\begin{align*} \quad A(-4 \ , \ 3) \ , \ B(-1 \ , \ 2) \ , \ C(3 \ , \ -1) \end{align*}$

について、次のものを求めよ。

$(1) \quad$ 点 $A$ と直線 $BC$ の距離

$(2) \quad$ $\triangle ABC$ の面積

問(1)の解答・解説

問(1)

次の $3$ 点

$\begin{align*} \quad A(-4 \ , \ 3) \ , \ B(-1 \ , \ 2) \ , \ C(3 \ , \ -1) \end{align*}$

について、次のものを求めよ。

点 $A$ と直線 $BC$ の距離

例題と問を比較してみましょう。問では、例題(1)，(2)が省略されています。

入試レベルになると、必要な作業があるにも関わらず、その作業を省略したような問題が出題されます。小問どうしの関係をしっかりと把握しておきましょう。

点Ａと直線ＢＣの距離を求めるには、直線ＢＣの方程式が必要でした。２点を通る直線の方程式に代入して、直線ＢＣの方程式を求めます。

問(1)の解答例 1⃣

直線 $BC$ は $2$ 点

$\begin{align*} \quad B(-1 \ , \ 2) \ , \ C(3 \ , \ -1) \end{align*}$

を通るので

$\begin{align*} &\quad \left(-1-2 \right)\left\{x-\left(-1 \right) \right\}-\left\{ 3-\left(-1 \right) \right\}\left(y-2 \right)=0 \\[ 7pt ] &\quad -3\left(x+1 \right)-4\left(y-2 \right)=0 \end{align*}$

よって

$\begin{align*} \quad 3x+4y-5=0 \end{align*}$

図に直線の方程式を追記しておきましょう。

点Ａと直線ＢＣの距離を求めます。点と直線の距離の式に代入します。

問(1)の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 3x+4y-5=0 \end{align*}$

点 $A$ と直線 $BC$ の距離を $d$ とすると

$\begin{align*} \quad d &= \frac{| 3 \cdot (-4)+4 \cdot 3-5 |}{\sqrt{ 3^{2}+4^{2}} } \\[ 7pt ] &= \frac{| -5 |}{\sqrt{9+16}} \end{align*}$

よって

$\begin{align*} \quad d=\frac{5}{5}=1 \end{align*}$

これは点 $A$ から $BC$ に下した垂線の長さに等しい。

問(2)の解答・解説

問(2)

次の $3$ 点

$\begin{align*} \quad A(-4 \ , \ 3) \ , \ B(-1 \ , \ 2) \ , \ C(3 \ , \ -1) \end{align*}$

について、次のものを求めよ。

$\triangle ABC$ の面積

三角形の面積を底辺の長さと高さを用いて求めるのであれば、問(1)を解いただけでは足りません。底辺の長さを求めていないからです。

２点間の距離の式に代入して、底辺である線分ＢＣの長さを求めます。

問(2)の解答例 1⃣

線分 $BC$ の長さは $2$ 点

$\begin{align*} \quad B(-1 \ , \ 2) \ , \ C(3 \ , \ -1) \end{align*}$

間の距離に等しいので

$\begin{align*} \quad BC &= \sqrt{\left\{ 3-(-1) \right\}^{2}+\left(-1-2 \right)^{2}} \\[ 7pt ] &= \sqrt{16+9} \end{align*}$

$BC \gt 0$ より

$\begin{align*} \quad BC=5 \end{align*}$

△ＡＢＣの底辺の長さ、高さが分かったので、面積を求めます。

問(2)の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 7pt ] &\quad BC=5 \end{align*}$

$\triangle {ABC}$ の面積は

$\begin{align*} \quad \triangle ABC &= \frac{1}{2} \cdot BC \cdot d \\[ 7pt ] &= \frac{1}{2} \cdot 5 \cdot 1 \end{align*}$

よって

$\begin{align*} \quad \triangle ABC=\frac{5}{2} \end{align*}$

問(2)の別解例

問(1)を無視して、問(2)を単独で解くこともできます。

点Ａが原点に重なるように平行移動させると、２点Ｂ，Ｃはそれぞれｘ軸方向に４、ｙ軸方向に－３だけ平行移動します。

平行移動後の２点Ｂ’，Ｃ’の座標を用いて、三角形の面積を求めます。

問(2)の別解例

点 $A(-4 \ , \ 3)$ が原点 $O(0 \ , \ 0)$ に重なるように $\triangle {ABC}$ を平行移動させると

$\begin{align*} \quad (-1+4 \ , \ 2-3) \ , \ (3+4 \ , \ -1-3) \end{align*}$

より、 $2$ 点 $B \ , \ C$ はそれぞれ

$\begin{align*} \quad B'(3 \ , \ -1) \ , \ C'(7 \ , \ -4) \end{align*}$

に平行移動する。

このとき

$\begin{align*} \quad \triangle ABC=\triangle OB’C’ \end{align*}$

であるので、 $\triangle ABC$ の面積は

$\begin{align*} \quad \triangle ABC &= \frac{1}{2}| 3 \cdot (-4)-7 \cdot (-1)| \\[ 7pt ] &= \frac{1}{2} \cdot 5 \end{align*}$

よって

$\begin{align*} \quad \triangle ABC=\frac{5}{2} \end{align*}$

頂点の座標を用いた三角形の面積の式は、かなり便利な式です。時間短縮だけでなく、検算にも使えるので、ぜひともマスターしておきたい式です。

Recommended books

さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。

難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。

傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。

おすすめ

◆特長◆

大学入試の基本となる問題を扱った問題集です。問題数は１３８問です。

問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。

問題編冊子４４頁、解答編冊子２２４頁の構成となっています。

◆自分にあったレベルが選べる！◆

基礎レベル

共通テストレベル

私大標準・国公立大レベル

私大上位・国公立大上位レベル

私大標準・国公立大レベル

私大上位・国公立大上位レベル