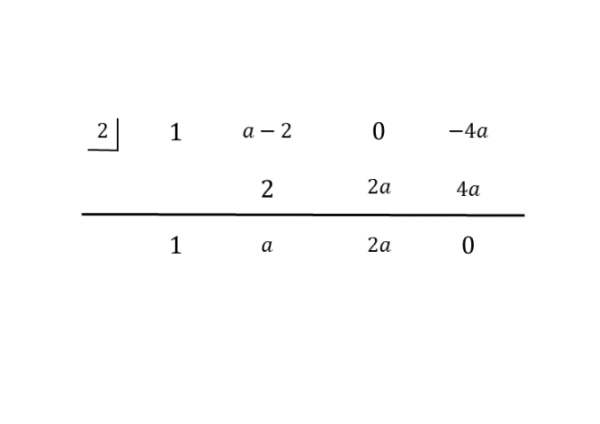数学２
３次方程式が２重解をもつ条件を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
$3$ 次方程式
\begin{equation*}
\quad x^{\scriptsize{3}}+(a-2)x^{\scriptsize{2}}-4a=0
\end{equation*}
が $2$ 重解をもつように定数 $a$ の値を定め、そのときの解をすべて求めよ。
問の解答・解説
３次方程式を扱った問題なので、まず因数分解することを考えましょう。また、定数ａの値が分かったら、３次方程式の解を確認することも忘れないようにしましょう。
剰余の定理や因数定理を利用して、因数となる１次式を見つけます。方程式の左辺をよく観察しましょう。意外と簡単に因数となる１次式が分かります。
問の解答例 1⃣
\begin{align*}
&\quad f(x)=x^{\scriptsize{3}}+\left(a-2 \right) x^{\scriptsize{2}}-4a \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad f(2)=2^{\scriptsize{3}}+\left(a-2 \right) \cdot 2^{\scriptsize{2}}-4a=0 \\[ 7pt ]
&\text{より、$f(x)$ は $x-2$ を因数にもつ。}
\end{align*}
因数となる１次式が分かったら、組立除法で３次式を割り算します。組立除法の結果は以下の通りです。３次式には１次の項がないことに注意しましょう。１次の項がないので、係数は０と考えます。
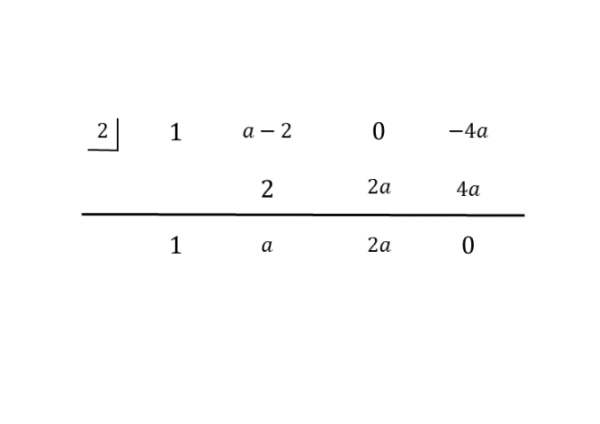問の組立除法 ３次式を因数分解できたら、与えられた３次方程式を因数分解した形にします。この因数分解の結果から、解を求めるための方程式を新たに導きます。
問の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{より、$f(x)$ は $x-2$ を因数にもつ。} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad f(x)=\left(x-2 \right) \left(x^{\scriptsize{2}}+ax+2a \right) \\[ 7pt ]
&\text{より、方程式は} \\[ 5pt ]
&\quad \left(x-2 \right) \left(x^{\scriptsize{2}}+ax+2a \right)=0 \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad x-2=0 \quad \text{または} \quad x^{\scriptsize{2}}+ax+2a=0
\end{align*}
３次方程式の解の１つは、１次方程式からすぐに分かります。この解をもとに場合分けをして、２重解をもつときの条件、言い換えると定数ａの値を求めます。
まず、２次方程式が重解をもつときです。ただし、１次方程式の解とは異なることも忘れないようにしましょう。
問の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x-2=0 \quad \text{または} \quad x^{\scriptsize{2}}+ax+2a=0 \\[ 7pt ]
&\text{[１] $x^{\scriptsize{2}}+ax+2a=0$ が $2$ ではない重解をもつ} \\[ 5pt ]
&\text{判別式を $D$ とすると} \\[ 5pt ]
&\quad D=0 \quad \text{かつ} \quad 2^{\scriptsize{2}}+a \cdot 2+2a \neq 0 \\[ 7pt ]
&\text{を満たせばよい。ここで} \\[ 5pt ]
&\quad D=a^{\scriptsize{2}}-8a=a \left(a-8 \right) \\[ 7pt ]
&\text{より、$D=0$ とすると} \\[ 5pt ]
&\quad a= 0 \ , \ 8 \\[ 7pt ]
&\text{これは $a+1 \neq 0$ を満たす。}
\end{align*}
誤って３重解にならないように、２次方程式がｘ＝２を解にもたないという条件を付けています。判別式の条件だけでは、２次方程式が重解をもつことは言えても、ｘ＝２を解にもたないことは言えないからです。
定数ａの値が分かったので、このときの残りの解、つまり２次方程式の重解を求めます。
問の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{$a=0$ のとき、$2$ 次方程式は} \\[ 5pt ]
&\quad x^{\scriptsize{2}}=0 \\[ 7pt ]
&\text{となるので、重解は $x=0$} \\[ 5pt ]
&\text{また、$a=8$ のとき、$2$ 次方程式は} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+8x+16=0 \\[ 7pt ]
&\text{となるので、重解は $x=-4$}
\end{align*}
次は、２次方程式の解の１つが２となる（１次方程式の解と同じになる）ときです。もちろん、２次方程式の残りの解は２になってはいけません。
問の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{[２] $x^{\scriptsize{2}}+ax+2a=0$ の解の $1$ つが $2$ で、他の解が $2$ ではない} \\[ 5pt ]
&\text{$x=2$ が解であるので} \\[ 5pt ]
&\quad 2^{\scriptsize{2}}+a \cdot 2+2a= 0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a+1=0 \quad \text{すなわち} \quad a=-1 \\[ 7pt ]
&\text{このとき、$2$ 次方程式は} \\[ 5pt ]
&\quad x^{\scriptsize{2}}-x-2=0 \\[ 7pt ]
&\text{となるので} \\[ 5pt ]
&\quad \left(x+1 \right) \left(x-2 \right)=0 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x=-1 \ , \ 2 \\[ 7pt ]
&\text{これは、他の解が $2$ ではないので適する。} \\[ 5pt ]
&\text{[１]，[２]より} \\[ 5pt ]
&\quad a=-1 \quad \text{のとき} \quad x=2 \ \text{（重解）} \ , \ -1 \\[ 7pt ]
&\quad a=0 \quad \text{のとき} \quad x=0 \ \text{（重解）} \ , \ 2 \\[ 7pt ]
&\quad a=8 \quad \text{のとき} \quad x=-4 \ \text{（重解）} \ , \ 2
\end{align*}
定数ａの値が小さい順に書き並べています。解いた順番と前後するので注意しましょう。
また、３次方程式が２重解をもつのは３通りあり、そのときの解も求めなければなりません。定数ａの値に対応させてそのときの解を書き並べましょう。いい加減な記述だと最後に混乱するので、記述の仕方を工夫しましょう。
組立除法が上手くいかないとき
問の３次式あっても、最低次数の文字（ここでは定数ａ）について整理すると、３次式を因数分解できます。
最低次数の文字に注目して因数分解する
\begin{align*}
&\quad x^{\scriptsize{3}}+(a-2)x^{\scriptsize{2}}-4a=0 \\[ 7pt ]
&\text{方程式の左辺を $a$ について整理すると} \\[ 5pt ]
&\quad x^{\scriptsize{3}}-2x^{\scriptsize{2}}+a \left(x^{\scriptsize{2}}-4 \right)=0 \\[ 7pt ]
&\text{さらに変形すると} \\[ 5pt ]
&\quad x^{\scriptsize{2}} \left(x-2 \right)+a\left(x+2 \right) \left(x-2 \right)=0 \\[ 7pt ]
&\text{共通因数 $x-2$ でくくると} \\[ 5pt ]
&\quad \left(x-2 \right) \left\{x^{\scriptsize{2}}+a\left(x+2 \right) \right\}=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad \left(x-2 \right) \left(x^{\scriptsize{2}}+ax+2a \right)=0
\end{align*}
２次方程式の重解の求め方
２次方程式の重解を求めるとき、素直に方程式を解く人が意外と多いかもしれません。間違ってはいませんが、その解き方は効率の悪い解き方です。マーク形式などの時間に余裕がない試験では、方程式を解くという基本的な解法はおすすめしません。
２次方程式が重解をもつことが分かっているとき、その重解は以下のようになることが分かっています。
２次方程式の重解
\begin{align*}
&\text{$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ が重解をもつとき、} \\[ 5pt ]
&\text{その重解は} \\[ 5pt ]
&\quad x=-\frac{b}{2a}
\end{align*}
このことを知っておくと、方程式をわざわざ解く必要がなく、時間短縮になります。暗算で解けるので、とても便利です。
本当に上述の解となるのかを確認してみましょう。
２次方程式の重解を実際に求めてみる
\begin{align*}
&\text{$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ の判別式を $D$ とする。} \\[ 5pt ]
&\text{重解をもつとき $D=0$ となるので} \\[ 5pt ]
&\quad b^{\scriptsize{2}}-4ac=0 \\[ 5pt ]
&\text{$a \neq 0$ より} \\[ 5pt ]
&\quad c=\frac{b^{\scriptsize{2}} }{4a} \\[ 5pt ]
&\text{これを $2$ 次方程式に代入すると} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+\frac{b^{\scriptsize{2}} }{4a}=0 \\[ 5pt ]
&\text{整理して因数分解すると} \\[ 5pt ]
&\quad 4a^{\scriptsize{2}}x^{\scriptsize{2}}+4abx+b^{\scriptsize{2}} =0 \\[ 5pt ]
&\quad \left(2ax+b \right)^{\scriptsize{2}} =0 \\[ 5pt ]
&\text{よって} \\[ 5pt ]
&\quad 2ax+b =0 \\[ 5pt ]
&\text{したがって、$2$ 次方程式が重解をもつとき、その解は} \\[ 5pt ]
&\quad x=-\frac{b}{2a}
\end{align*}
上述のことから、２次方程式が重解をもつとき、その解は２次の項と１次の項の係数だけ決まります。この性質を上手に利用して、方程式を解かずに済ませましょう。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
共通テスト対策として必要なことをすべて備えた理想の予想問題集が完成
単に問題を解くだけでなく、その背景にある考え方や知識まで掘り下げて解説。「分析編」では、過去2回の試行調査（プレテスト）から見えてきた共通テストの出題傾向を詳細に分析するだけでなく、学習法や学習姿勢などの具体的な対策まで説明。本番でそのまま出そうな予想問題と、くわしい解説がセットになった至高の実践型問題集。
もくじ
- 本冊
- 別冊
- 試行調査：２回分（2017年度／2018年度）
- 予想問題：２回分
公式サイトでは、一部の内容を閲覧できます。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- ３次方程式の問題では、因数分解を優先しよう。
- ３次方程式が２重解をもち方は２通りある。
- １次式の因数を見つけて因数分解しよう。
- ２次方程式の重解は公式を用いて求めよう。
- ３重解にならないように、他の解も確認しよう。
