集合と論理|必要条件と十分条件、同値について

十分条件や必要条件を扱った問題を解いてみよう
次の問題を考えてみましょう。
問1(1)の解答・解説
問1(1)
次の□の中には、「必要条件である」「十分条件である」「必要十分条件である」のうち、最も適するものをいれよ。ただし、文字はすべて実数とする。
$x=1$ は、$x^{\scriptsize{2}}=1$ であるための□。
問1(1)は、x=1がx2=1にとってどんな条件かを求める問題です。
x=1を条件p、x2=1を条件qとして、2つの命題「p⇒q」と「q⇒p(p⇐q)」の真偽をそれぞれ考えます。
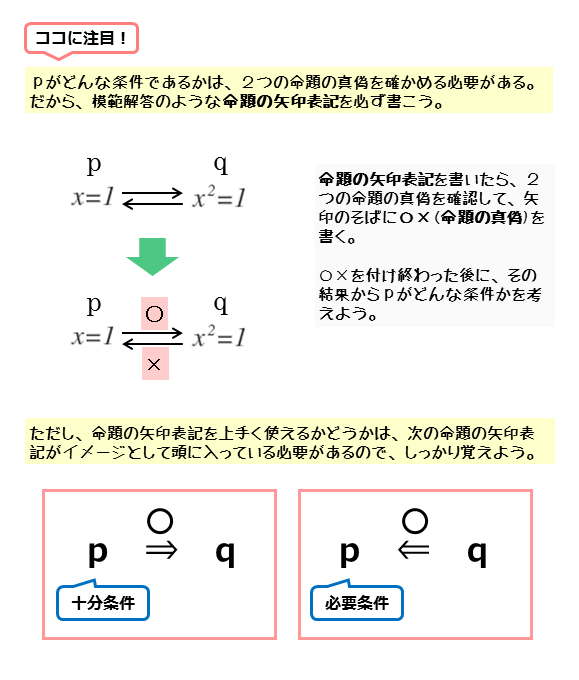
2つの条件p,qの間に左右両方の矢印を書き(例p⇆q)、2つの命題「p⇒q」と「q⇒p(p⇐q)」の真偽を順番に調べます。
命題「p⇒q」の真偽を調べます。
問1(1)の解答例 1⃣
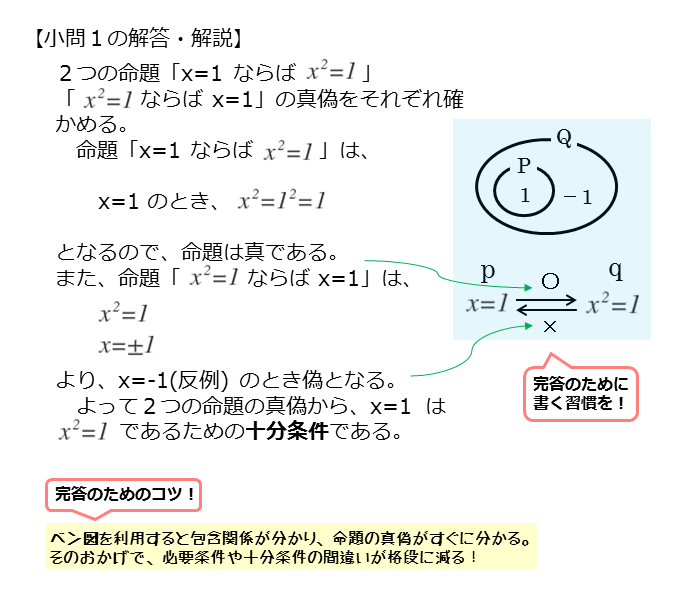
\begin{align*} \quad p: \ x=1 \ \Rightarrow \ q: \ x^{\scriptsize{2}} = 1 \end{align*}の真偽を調べる。
$x = 1$ のとき
\begin{align*} \quad x^{\scriptsize{2}} = 1 \end{align*}は成り立つので
\begin{align*} \quad p \Rightarrow q \ \text{は真} \end{align*}真偽が分かったら、矢印の上にマルバツをつけておきます。
次に、命題「q⇒p(p⇐q)」の真偽を調べます。こちらは少し注意する必要があります。
問1(1)の解答例 2⃣
\begin{align*} \quad p: \ x=1 \ \Leftarrow \ q: \ x^{\scriptsize{2}} = 1 \end{align*}の真偽を調べる。
$x^{2} = 1$ すなわち $x = \pm 1$ のとき
\begin{align*} \quad x=1 \end{align*}がつねに成り立つとは限らない。
反例は $x=-1$ のとき
これより
\begin{align*} \quad p \Leftarrow q \ \text{は偽} \end{align*}よって、$p$ は $q$ であるための十分条件である。
条件qは2次方程式で与えられています。このままでは、条件qを満たす変数xの値、言い換えると集合に属する要素が分かりません。
要素が分からないと、集合の包含関係を調べることができません。変数xの値(=要素)を明らかにするために2次方程式を解き、それから命題の真偽を調べます。
条件を満たす変数の値(=要素)をはっきりさせてから、命題の真偽を調べよう。
命題の真偽を調べる流れを図解すると以下のようになります。
命題の真偽は、矢印の上または下のマルバツで分かります。その結果をもとにp,qの関係を考えます。
命題「p⇒q」が真で、命題「q⇒p(p⇐q)」が偽です。
このことから、pはq(であるため)の十分条件ではありますが、必要条件ではありません。
問1(1)のポイントと解答例をまとめると以下のようになります。解答例ではベン図も使っているので、命題の真偽をより簡単に調べることができています。
条件p,qが真となる変数の値を求めて、それを集合や要素に置き換えよう。集合の包含関係で命題の真偽を調べる方が、与えられた条件のままで調べるよりも確実でラク。
問1(2)の解答・解説
問1(2)
次の□の中には、「必要条件である」「十分条件である」「必要十分条件である」のうち、最も適するものをいれよ。ただし、文字はすべて実数とする。
$x=3$ は、$2x-6=0$ であるための□。
問1(2)は、x=3が2x-6=0にとってどんな条件かを求める問題です。
問1(1)と同じように、x=3を条件p、2x-6=0を条件qとして、2つの命題「p⇒q」と「q⇒p(p⇐q)」の真偽をそれぞれ考えます。
注意したいのは、条件qが1次方程式で与えられていることです。変数xの値が不明なので、方程式を解いて解を求めておきます。
問1(2)の解答例
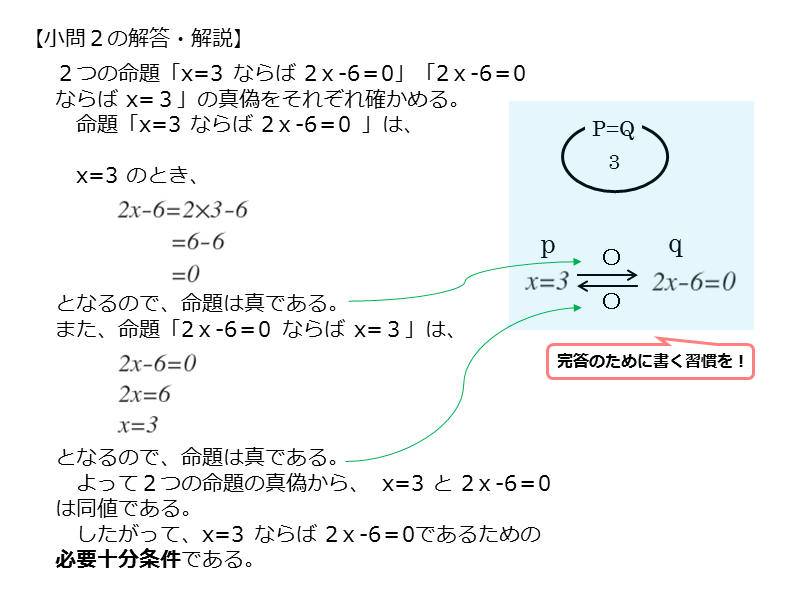
とする。
条件 $q$ が真となる変数 $x$ の値は
\begin{align*} \quad x = 3 \end{align*}これは条件 $p$ と同値である。
よって、$p$ は $q$ であるための必要十分条件である。
条件qが真となる変数xの値は、与えられた1次方程式の解です。解はx=3となり、これは条件pと全く同じになります。
これより、集合と要素が一致するので、条件p,qは同値であることが分かります。
問1(2)のポイントと解答例をまとめると以下のようになります。
条件が真となる変数の値を使って、命題の真偽を調べよう。
問1(3)の解答・解説
問1(3)
次の□の中には、「必要条件である」「十分条件である」「必要十分条件である」のうち、最も適するものをいれよ。ただし、文字はすべて実数とする。
$x \geqq 1$ は、$x \geqq 2$ であるための□。
問1(3)は、x≧1がx≧2にとってどんな条件かを求める問題です。
(1),(2)と同じように、x≧1を条件p、x≧2を条件qとして、2つの命題「p⇒q」と「q⇒p(p⇐q)」の真偽をそれぞれ考えます。
命題「p⇒q」の真偽を調べます。
問1(3)の解答例 1⃣
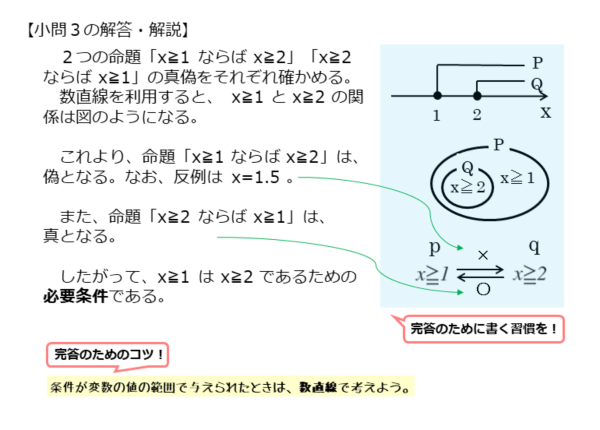
\begin{align*} \quad p: \ x \geqq 1 \ \Rightarrow \ q: \ x \geqq 2 \end{align*}の真偽を調べる。
条件 $p$ を満たす実数 $x$ が
\begin{align*} \quad x = 1.5 \end{align*}であるとき、条件 $q$ を満たさないので
\begin{align*} \quad p \Rightarrow q \ \text{は偽} \end{align*}真偽が分かったら、矢印の上にマルバツをつけておきます。
次に、命題「q⇒p(p⇐q)」の真偽を調べます。
問1(3)の解答例 2⃣
\begin{align*} \quad p: \ x \geqq 1 \ \Leftarrow \ q: \ x \geqq 2 \end{align*}の真偽を調べる。
条件 $q$ を満たす実数 $x$ は、すべて条件 $p$ を満たす。
よって
\begin{align*} \quad p \Leftarrow q \ \text{は真} \end{align*}よって、$p$ は $q$ であるための必要条件である。
2つの条件p,qは、不等式で与えられています。この場合、ベン図よりも数直線の方が、真偽を調べるのに向いています。
数直線で図解すれば分かるように、x≧1の方がx≧2よりも大きな範囲になります。これより、集合P,Qの包含関係はQ⊂Pとなります。
集合P,Qの包含関係から、命題「p⇒q」が偽で、命題「q⇒p(p⇐q)」が真になります。
問1(3)のポイントと解答例をまとめると以下のようになります。
条件が不等式で与えられていれば、数直線を使って命題の真偽を調べよう。
十分条件や必要条件を調べるとき、ベン図や数直線を上手に利用しましょう。集合どうしの包含関係が分かれば、命題の真偽も簡単に分かります。
Recommended books
大学進学を考えたとき、記述を重視した学習を日常的に行った方が良いでしょう。試験の難易度は、マーク形式よりも記述形式の方が高いからです。
また、記述では思考力や表現力などが必要で、それらを身に付けるのは一朝一夕には難しいことも理由の1つです。
記述の訓練は、基本的に教科書や参考書の例題を真似することから始まりますが、記号の使い分けや独特の表現などがあり、手探りで進めていくのは大変です。
そこでお勧めしたいのが以下の2冊です。記述の訓練に特化したテキストになります。
オススメその1
1冊目は『基礎からのジャンプアップノート 数学 記述式答案 書き方ドリル』で、数学に苦手意識のある人におすすめです。
数学Ⅰ+A+Ⅱ+Bの記述力の基礎力を固めるなら、まずはこのドリルから!!
問題編64ページ、別冊解答編32ページ
- 証明問題、場合分けの答案の書き方のコツがわかる
- 「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい
- 「例(手本)」→「Check!」→「練習問題」 まねる&繰り返すの流れで、記述力UP!
- 別冊「解答編」では、練習問題をくわしく解答
『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。
オススメその2
2冊目は『総合的研究 記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。
『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。
この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。
ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。
(中略)数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です(抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です)。
自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。
この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。
それでは、《伝える》レッスンをはじめましょう!(まえがきより)
著者が異なりますが、こちらも『総合的研究』シリーズです。
さいごに、もう一度、頭の中を整理しよう
- 十分・必要条件は、2つの条件の関係を表す。
- 十分条件か必要条件かは、2つの命題「p⇒q」「p⇐q」の真偽を調べることで判定できる。
- 命題の真偽は、集合と要素に置き換えて包含関係を調べよう。
- 集合の包含関係はベン図を使って調べよう。
- 条件が不等式であれば、数直線を使おう。