データの分析|データの整理について

今回から数学1の「データの分析」について学習します。最初の単元は「データの整理」です。データのことやデータの整理について学習します。
新しい用語や定理などが出てくるので、できるだけ早く、そして正確に覚えましょう。
この単元で学習すること
「データの整理」では以下のような事柄を学習します。
データの整理で学習する事柄
- データについて
- 度数分布表
- ヒストグラム
データを扱うために色々な用語が定義されているので、1つずつ丁寧に確認していきましょう。
データについて
テストの得点や短距離走のタイムなどのように、ある集団を構成する人や物の特性を数量的に表す量のことを変量と言います。
また、調査や実験などで得られた変量の観測値や測定値の集まりのことをデータと言います。
変量とデータの一例
$A \ , \ B \ , \ C$ の $3$ 人が受けた数学のテストの得点が $70$ 点、$73$ 点、$87$ 点だったとすると
変量 … 数学のテストの得点
データ … $70$ 点、$73$ 点、$87$ 点
データの整理について
データが少ないうちは問題ありませんが、データが多くなってくると、そのままでは分析するのが困難になってきます。データを比較したり、傾向を分析したりするためには、データを整理することが必要になります。
データを整理するとき、データの値の範囲をいくつかの区間に区切ると扱いやすくなります。このときの区間のことを階級と言います。
また、区間の幅のことを階級の幅、階級の真ん中の値を階級値と言います。
いくつかの区間(階級)に区切ると、各データはその値に応じた階級に入ります。各階級に入ったデータの個数のことを度数と言います。
各階級ごとに度数が決まるので、これを表にまとめることができます。このように各階級に度数を対応させた表のことを度数分布表と言います。
そして、各階級の度数の全体に対する割合のことを、その階級の相対度数と言います。
度数分布表を用いてデータを整理しよう
たとえば、以下のような生徒20人の身長の測定値を度数分布表にまとめてみましょう。
【例】生徒20人の身長の測定値
\begin{align*} &\quad 172.1 \quad 165.3 \quad 158.2 \quad 174.2 \quad 155.3 \\[ 7pt ] &\quad 173.7 \quad 163.4 \quad 154.1 \quad 176.6 \quad 161.3 \\[ 7pt ] &\quad 175.8 \quad 152.7 \quad 176.6 \quad 167.9 \quad 166.8 \\[ 7pt ] &\quad 177.5 \quad 166.4 \quad 173.9 \quad 171.9 \quad 156.5 \end{align*}ただし、単位は $cm$ である。
階級の幅を5cm として度数分布表にまとめると、以下のようになります。
| 階級(cm) | 度数(人) |
| 175.0以上~180.0未満 | 4 |
| 170.0以上~175.0未満 | 5 |
| 165.0以上~170.0未満 | 4 |
| 160.0以上~165.0未満 | 2 |
| 155.0以上~160.0未満 | 3 |
| 150.0以上~155.0未満 | 2 |
| 計 | 20 |
問題によっては、階級値や相対度数が必要になる場合があります。そんなときは、以下のように自分で追記しておくと良いでしょう。
階級値は、階級の真ん中の値でした。175.0cm 以上~180.0cm 未満の階級であれば、階級値は177.5cm となります。
また、相対度数は、各階級の度数を度数の合計で割ったときの割合でした。175.0cm 以上~180.0cm 未満の階級であれば、相対度数は4÷20=0.2となります。
| 階級(cm) | 度数(人) | 階級値(cm) | 相対度数 |
| 175.0以上~180.0未満 | 4 | 177.5 | 0.2 |
| 170.0以上~175.0未満 | 5 | 172.5 | 0.25 |
| 165.0以上~170.0未満 | 4 | 167.5 | 0.2 |
| 160.0以上~165.0未満 | 2 | 162.5 | 0.1 |
| 155.0以上~160.0未満 | 3 | 157.5 | 0.15 |
| 150.0以上~155.0未満 | 2 | 152.5 | 0.1 |
| 計 | 20 | - | 1 |
このように度数分布表を用いると、データを整理することができます。
ヒストグラムを用いてデータを視覚化しよう
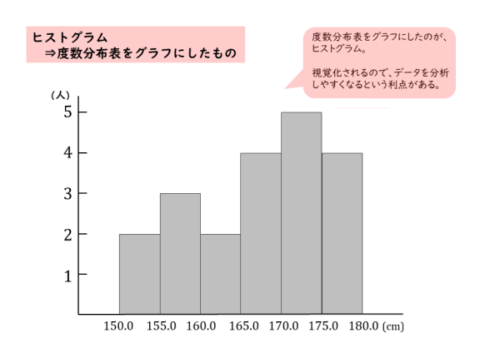
より視覚的にしたい場合、度数分布表をもとに階級と度数の関係をグラフで表します。このグラフのことをヒストグラムと言います。ヒストグラムで視覚化することによって、データをより分析しやすくなります。
度数分布表 ⇒ ヒストグラム
先程の身長の測定値についての度数分布表をヒストグラムで表すと、以下のようになります。
度数が大きくなればなるほど、長方形の高さが大きくなるので、どの階級の度数が大きいのか、あるいは小さいのかがひと目で分かります。
データを整理すると言えば、度数分布表を作ると捉えておこう。より視覚的にしたいならヒストグラム。
これまでに出てきた用語をまとめると、以下のようになります。
データの整理に関する用語
変量 … ある集団を構成する人や物の特性を数量的に表す量
データ … 調査や実験などで得られた変量の観測値や測定値の集まり
階級 … 各データの値の範囲を区切ったときの区間
階級の幅 … 区間の幅
階級値 … 階級の真ん中の値
度数 … 各階級に入ったデータの個数
度数分布表 … 各階級に度数を対応させた表
相対度数 … 各階級の度数の全体に対する割合
ヒストグラム … 度数分布表をグラフにしたもの
次は、度数分布表やヒストグラムを扱った問題を実際に解いてみましょう。