図形と方程式|平行四辺形の頂点の座標について

平行四辺形の頂点の座標を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
問の解答・解説
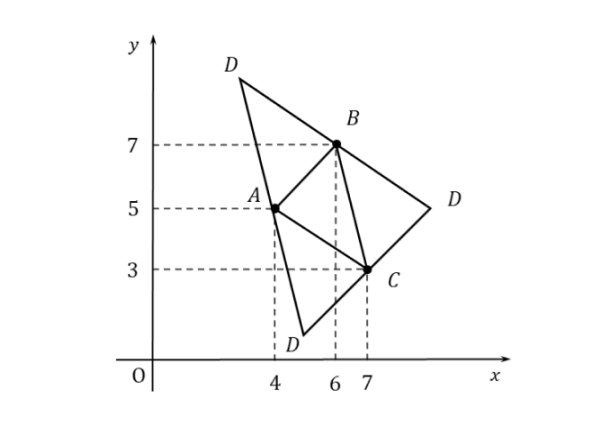
平行四辺形の名称がないので、頂点Dの座標は3通り考えられます。作図して確認しましょう。
例題と同じ要領で解きます。点Dの座標を定義して、3通りの平行四辺形を場合分けして解いていきます。
問の解答例 1⃣
それぞれの平行四辺形において、点Dの座標を求めます。2本の対角線の中点が一致することを利用して、方程式を導きます。
まず、平行四辺形ABCDの場合です。対角線は、2つの線分BD,ACです。
問の解答例 2⃣
次は、平行四辺形ABDCの場合です。対角線は、線分ADと線分BCです。
問の解答例 3⃣
さいごに、平行四辺形ADBCの場合です。対角線は、2つの線分CD,ABです。
問の解答例 4⃣
残りの頂点の位置から対角線を把握し、その中点の座標を用いて方程式を導きます。方程式と言っても、1次方程式なので計算量は多くありません。
残りの頂点の位置を把握できれば、間違うことはないでしょう。図を上手に利用して、頂点の位置を把握しましょう。
Recommended books
おすすめというよりも、ちょっと気になる書籍を紹介します。気になる人はぜひ一読してみて下さい。
オススメその1『東大の先生! 文系の私に超わかりやすく数学を教えてください!』
「中学生は決して読まないでください!!」という触れ込みの本書。それは、5~6時間で中学3年分の数学がほぼ終わってしまう「禁断の書」だからです。
本書は、中学・高校で数学に挫折してしまった大人のための「最速・最短で数学のやり直しができる本」です。しかし、中学生や高校生が全体像を掴むのに役立つのではないかと思います。
誰にでも必要な数学知識の基礎になる中学数学。
時間がない社会人のために、3年分で学ぶ内容を、ぎゅっと凝縮しました。
本書のために、つくられた「3つのゴール」を目指して問題を解くと、中学数学で習う最重要の単元がほぼすべて学べます。
東大人気教授の数学教室、開校です!
高校数学バージョンはこちらです。
オススメその2『数学の傑作を味わう 驚異の23のエッセンス』
数学の面白さと美しさを伝える23の傑作集。絵画の「モナ・リザ」に匹敵する数学の傑作を通して、 数学の面白さ、美しさ、可能性を知る、 最高の数学入門書。
本書のテーマは、絵画におけるモナ・リザや、物理学におけるE = mc^2に相当する、数学の傑作を紹介することです。
共通する特徴は、
(1)数学者以外にはあまり知られていないこと
(2)「証明」の考え方を教えてくれること
(3)高校までの数学で理解できること
(4)驚きの帰結であること
(5)実用と結びつくこと
本書によって、読者は、数学の面白さと美しさ、可能性を知るとともに、真に数学的な考え方をみにつけることがができるでしょう。
さいごにもう一度まとめ
- 平行四辺形の名称の有無を確認しよう。
- 図形の名称があれば、頂点の順序はただ1つに定まる。
- 図形の名称がなければ、頂点の順序を場合分けしよう。
- 平行四辺形の頂点を扱うときは、対角線の中点を利用しよう。
- 平行四辺形の2本の対角線の中点は一致する。