2次関数|2次不等式の解法について(応用編)

2次関数のグラフとx軸との共有点が0個の場合
グラフとx軸との共有点が0個の場合、2次関数においてy=0のときの2次方程式を考えてみましょう。
共有点が0個なので、2次方程式の実数解は0個です。つまり、2次方程式は実数解をもちません。
実数解をもたないということは、2次方程式を因数分解することも、解の公式で解を求めることもできません。
2次方程式を因数分解できなければ、解の公式を用いれば解くことができました。
しかし、2次方程式が実数解をもたない場合、解の公式を使っても無駄に労力を掛けるだけになります。ですから、少し解法を考える必要があります。
2次不等式の左辺を因数分解することができないと分かった場合、2次方程式を作ってすぐにその解を求める・・・という流れではなく、2次方程式を作って判別式の値を調べる・・・という流れで解きましょう。
因数分解できないとき、解の公式を用いる前に、判別式の値を調べよう。2次方程式が実数解をもたなければ、解の公式でも解けないので、実数解の有無を先に調べる方が効率的。
判別式の値を調べれば、共有点の個数が分かります。共有点があると分かれば、解の公式で解けば良いでしょう。ここでは共有点がないので、判別式の値は負の数になります。
値域に対応する定義域を考える
2次不等式を2次関数と値域に置き換えたとき、先ほどと同じように値域は4つのパターンが考えられます。
4パターンの値域
- y>0のとき
- y≧0のとき
- y<0のとき
- y≦0のとき
それぞれの場合で定義域を考えます。
値域がy>0のとき
値域がy>0のとき、値域に対応するグラフは、すべての部分が残ったグラフになります。
グラフを参考にすると、値域に対応する定義域はすべての実数です。ですから、2次不等式の解はすべての実数となります。
以下のように一般化されています。
2次不等式の解 5⃣
$2$ 次方程式
\begin{align*} \quad a{x}^{2}+bx+c = 0 \quad ( a \gt 0 ) \end{align*}が実数解をもたないとき、$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \gt 0 \end{align*}の解は、すべての実数
値域がy≧0のとき
値域がy≧0のとき、値域に対応するグラフは、すべての部分が残ったグラフになります。
グラフを参考にすると、値域に対応する定義域はすべての実数です。ですから、2次不等式の解はすべての実数となります。
以下のように一般化されています。
2次不等式の解 6⃣
$2$ 次方程式
\begin{align*} \quad a{x}^{2}+bx+c = 0 \quad ( a \gt 0 ) \end{align*}が実数解をもたないとき、$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \geqq 0 \end{align*}の解は、すべての実数
値域がy<0のとき
値域がy<0のとき、値域に対応するグラフはありません。グラフが値域に含まれないからです。
グラフを参考にすると、値域に対応する定義域は存在しません。ですから、2次不等式の解は解なしとなります。
以下のように一般化されています。
2次不等式の解 7⃣
$2$ 次方程式
\begin{align*} \quad a{x}^{2}+bx+c = 0 \quad ( a \gt 0 ) \end{align*}が実数解をもたないとき、$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \lt 0 \end{align*}の解は、解なし
値域がy≦0のとき
値域がy≦0のとき、値域に対応するグラフはありません。y<0のときと同じく、グラフが値域に含まれません。
グラフを参考にすると、値域に対応する定義域は存在しません。ですから、2次不等式の解は解なしとなります。
以下のように一般化されています。
2次不等式の解 8⃣
$2$ 次方程式
\begin{align*} \quad a{x}^{2}+bx+c = 0 \quad ( a \gt 0 ) \end{align*}が実数解をもたないとき、$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \leqq 0 \end{align*}の解は、解なし
共有点が1個または0個のときの2次不等式の解のまとめ
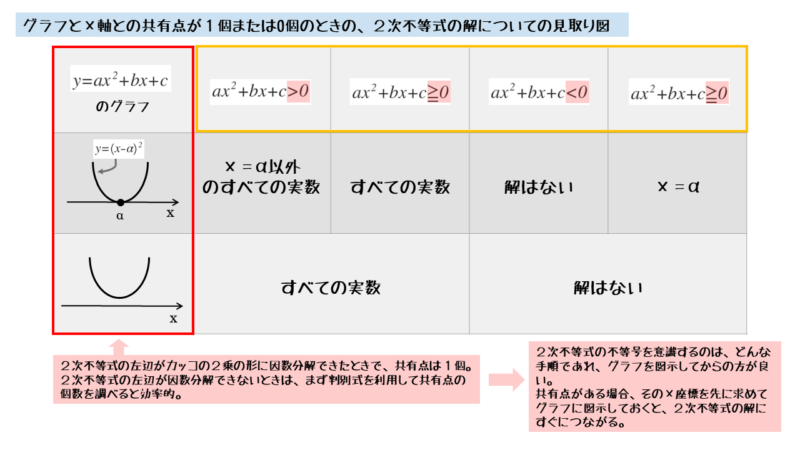
グラフとx軸との共有点が1個または0個のとき、2次不等式の解がどうなるかを一覧表にまとめると以下のようになります。
共有点が1個または0個のとき、グラフなしで解くと間違えやすいので、図示しながら解きましょう。
次は2次不等式を扱った問題を実際に解いてみましょう。