中学数学｜正負の数の乗除算について

09/25/2021中学数学

正負の数の加減算の次は、正負の数の乗除算を攻略します。

乗除算とは、乗算（乗法）と除算（除法）をまとめた言い方です。簡単な言い方だと、掛け算や割り算のことです。

加減算では減算を加算に置き換えるので、減算する必要がなくなりました。

それに対して、正負の数の乗除算ではどうなのでしょうか。その辺りのことを意識しながら学習しましょう。

正負の数の乗除算

加減算のときと同じように、乗除算でも具体例を挙げながら言葉に置き換えて考えてみます。

「速さ」×「時間」＝「道のり」で分かるのは絶対値

道のり、速さ、時間を例に正負の数の乗算について考えます。

たとえば、Ａさんが自転車に乗ってある目的地に行くとします。速さは分速１０mとします。

道のりは速さと時間の積で求めることができるので、たとえば３分前だろうと、３分後だろうとしても、道のりは１０×３＝３０ｍです。

つまり、この計算結果で分かるのは、分速１０mで３分間だけ移動した道のりです。

では、３分前や３分後の位置を知りたい場合はどうでしょうか。

この場合、進む向きが分からないので、この計算結果だけでは位置を特定することができません。

計算結果だけでなく３分前や３分後の条件を加味して、現在地から３０mだけ先や現在地よりも３０m手前というふうに、２段階のステップを踏む必要があります。

これまでのように正負の数を使わない計算では、移動距離、つまり大きさ（絶対値のこと）だけを求める計算で、現在地との相対的な位置を求めることができません。

符号の定義をしっかりと

今度は正負の数を使って考えてみます。

正負の数では符号を用いるので、符号の示す向きを予め決めておく必要があります。現在地（出発地）を基準の位置０ｍとして、現在地から右向きを正の向き、その左向きを負の向きとします。

このとき、正の向きに分速１０mは分速＋１０m、負の向きであれば分速－１０mと表せます。

また、現在地の時刻を基準とすると、現在地の時刻に対して、３分後ならば＋３分、３分前は－３分と表せます。

このように正負の数を用いると、数にいくつかの意味を持たせることができます。符号の扱いに慣れると、数式を扱うのが非常に楽になります。

正負の数の乗算

正の数どうしの乗算（分速＋１０m，＋３分）

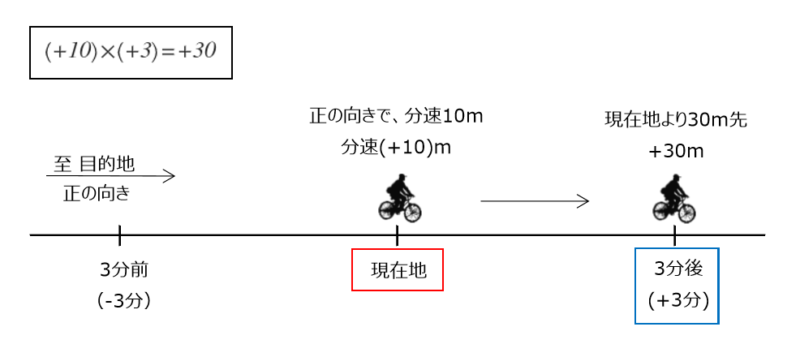
Ａさんは現在地から右向きに向かって分速１０m（分速＋１０ｍ）で移動するとします。Ａさんの現在地に対する３分後（＋３分）の位置を考えてみます。

先ほど求めたように、分速１０mで３分間だけ移動したときの道のりは３０mでした。ですから３分後のとき、現在地に対して右向きに３０mの位置（＋３０ｍ）にいます。

このことを正負の数を用いると、「分速＋１０mで＋３分のとき、(現在地に対して)＋３０mの位置にいる」と表せます。

このように正負の数を用いると、基準に対する向きと距離、つまり基準に対する位置が分かるようになります。

また、この結果から、以下のような乗算の式が得られます。

道のり・速さ・時間の例から分かること 1⃣

\begin{align*} \quad (+10) \times (+3) =+30 \end{align*}

$2$ 数の符号が同符号（＋）のとき、積の符号は正の符号（＋，プラス）

$2$ 数の符号が同符号のとき、積の絶対値は $2$ 数の絶対値の積

物理でも、直線運動などでは正負の数を利用するので、予備知識として持っておくと良いでしょう。

正の数と負の数の乗算（分速＋１０m，－３分）

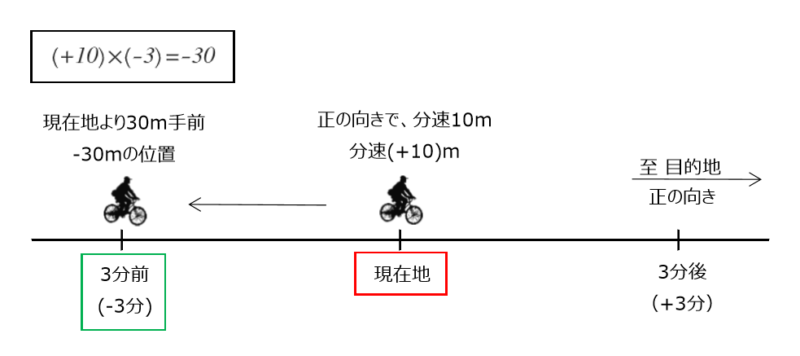
今度は現在地に到着する３分前（－３分）の位置を考えます。

道のりは３０mでしたが、３分前なので現在地に対して左向きに３０mの位置（－３０ｍ）にいます。

このことを正負の数を用いると、「分速＋１０mで－３分のとき、(現在地に対して)－３０mの位置にいる」と表せます。

また、この結果から、以下のような乗算の式が得られます。

道のり・速さ・時間の例から分かること 2⃣

\begin{align*} \quad (+10) \times (-3) =-30 \end{align*}

$2$ 数の符号が異符号（＋と－）のとき、積の符号は負の符号（－，マイナス）

$2$ 数の符号が異符号のときでも、積の絶対値は $2$ 数の絶対値の積

負の数と正の数の乗算（分速－１０m，＋３分）

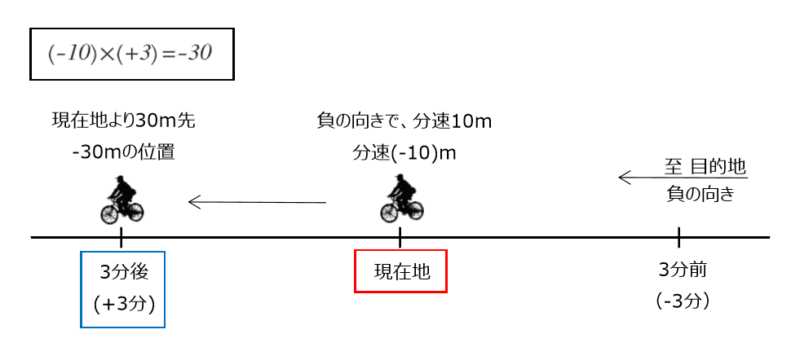
さらにＡさんは、現在地から左向きに向かって分速１０m（分速－１０ｍ）で移動するとします。Ａさんの現在地に対する３分後（＋３分）の位置を考えてみます。

なお正の向きと負の向きの設定は変わりませんが、自転車の進む向きに合わせて時の前後が変わることに注意しましょう。

道のりは３０mですが、３分後なので現在地に対して左向きに３０mの位置（－３０ｍ）にいます。

このことを正負の数を用いると、「分速－１０mで＋３分のとき、(現在地に対して)－３０mの位置にいる」と表せます。

また、この結果から、以下のような乗算の式が得られます。

道のり・速さ・時間の例から分かること 3⃣

\begin{align*} \quad (-10) \times (+3) =-30 \end{align*}

$2$ 数が異符号（－と＋）のとき、積の符号は負の符号（－，マイナス）

$2$ 数が異符号のときでも、積の絶対値は $2$ 数の絶対値の積

負の数どうしの乗算（分速－１０m，－３分）

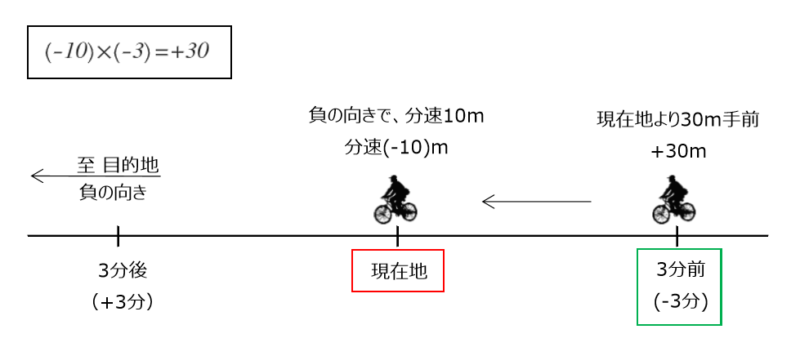
同様にＡさんは左向きに分速１０m（分速－１０ｍ）で移動しますが、Ａさんの現在地に対する３分前（＋３分）の位置を考えてみます。

道のりは３０mとなり、３分前なので現在地に対して右向きに３０mの位置（＋３０ｍ）にいることになります。

このことを正負の数を用いると、「分速－１０mで－３分のとき、現在地に対して＋３０mの位置にいる」と表せます。

また、この結果から、以下のような乗算の式が得られます。

道のり・速さ・時間の例から分かること 4⃣

\begin{align*} \quad (-10) \times (-3) =+30 \end{align*}

$2$ 数が同符号（－と－）のとき、積の符号は正の符号（＋，プラス）

$2$ 数が同符号のとき、積の絶対値は $2$ 数の絶対値の積

乗算から分かるルール

「速さ」×「時間」＝「道のり」の公式に正負の数を用いると、向きと基準からの距離、つまり基準に対する位置という情報が得られます。

先ほどの例から導かれた乗算は以下のようになりました。

道のり・速さ・時間の例から分かること（まとめ）

\begin{align*} &1. \quad (+10) \times (+3) =+30 \\[ 7pt ] &2. \quad (+10) \times (-3) =-30 \\[ 7pt ] &3. \quad (-10) \times (+3) =-30 \\[ 7pt ] &4. \quad (-10) \times (-3) =+30 \end{align*}

この結果から、正負の数の乗算には以下のような規則性があります。

正負の数の乗算の規則性

２数の符号が同符号のとき、積の符号は正の符号（＋，プラス）
２数の符号が異符号のとき、積の符号は負の符号（－，マイナス）
積の数字（＝絶対値）は、２数の絶対値の積。

この規則性を利用すれば、正負の数の乗算では、加算と同様に符号と絶対値を分けて扱うことができます。

正負の数の乗算では、符号と絶対値を分けて扱おう。

正負の数の除算

正負の数の除算を考えます。除算では、割る数の逆数を取れば乗算に置き換えることができます。

ですから、除算でも乗算に置き換えてしまえば、乗算の規則性を利用して計算できるということです。

除算は乗算に置き換えて規則性を利用する

\begin{align*} 1. \quad &\left(+30 \right) \div \left(+3 \right) \\[ 7pt ] = \ &\left(+30 \right) \times \left(+\frac{1}{3} \right) \\[ 7pt ] = \ &+\left(30 \times \frac{1}{3} \right) \\[ 7pt ] = \ &+10 \\[ 15pt ] 2. \quad &\left(+30 \right) \div \left(-3 \right) \\[ 7pt ] = \ &\left(+30 \right) \times \left(-\frac{1}{3} \right) \\[ 7pt ] = \ &-\left(30 \times \frac{1}{3} \right) \\[ 7pt ] = \ &-10 \\[ 15pt ] 3. \quad &\left(-30 \right) \div \left(+3 \right) \\[ 7pt ] = \ &\left(-30 \right) \times \left(+\frac{1}{3} \right) \\[ 7pt ] = \ &-\left(30 \times \frac{1}{3} \right) \\[ 7pt ] = \ &-10 \\[ 15pt ] 4. \quad &\left(-30 \right) \div \left(-3 \right) \\[ 7pt ] = \ &\left(-30 \right) \times \left(-\frac{1}{3} \right) \\[ 7pt ] = \ &+\left(30 \times \frac{1}{3} \right) \\[ 7pt ] = \ &+10 \end{align*}

除算での規則性は乗算と同じなので、除算のままで計算することもできます。

数だけの除算であればそのままでも構いませんが、文字を含む数式になると簡単ではありません。ですから、乗除算を乗算に統一する計算に慣れておきましょう。