中学数学|正負の数の乗除算を解いてみよう

今回は、正負の数の乗除算を解いてみましょう。
符号の組み合わせに規則性があったので、それを思い出しながら演習しましょう。また、計算過程にも注目して、計算の流れを把握しましょう。
乗除算では乗算が基本
次のような乗除算を考えます。
例題
\begin{align*} &(1) \quad \left(+2.1 \right) \times \left(-0.8 \right) \\[ 7pt ] &(2) \quad \left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \\[ 7pt ] &(3) \quad 10 \div \left(-6 \right) \\[ 7pt ] &(4) \quad \left(-\frac{2}{5} \right) \div \left(-\frac{2}{3} \right) \end{align*}正負の数の乗算や除算の基本的な流れ
式をよく観察すると、前半の2問が乗算で、後半の2問が除算だと分かります。
乗算の基本的な流れ
乗算の基本的な流れは以下のようになります。
乗算の基本的な流れ
- 符号の組合せを見て、答え(積)の符号を決める。
- 数字(絶対値)だけで乗算して、答え(積)の数字(絶対値)を求める。
乗算では、計算記号と符号を見間違えることはないので、符号の扱いに注意して解きます。また、数字(絶対値)の乗算では符号を気にしなくて良いので、算数のときと同じように計算できます。
除算の基本的な流れ
除算の基本的な流れは以下のようになります。
除算の基本的な流れ
- 除算を乗算に置き換える。
- 符号の組み合わせを見て、答え(積)の符号を決める。
- 数字(絶対値)だけで乗算して、答え(積)の数字(絶対値)を求める。
除算では、乗算に置き換える作業が最初に入っています。ここがしっかりできれば、乗算と同じ流れになります。
除算は、乗算に置き換えよう。
符号の規則性や数字(絶対値)の扱い方
乗除算を乗算に統一した後は、符号と数字(絶対値)を分けて扱うのがコツです。
答え(積)の符号と数字(絶対値)は、以下のような規則性で求めることができます。
符号と数字の規則性
- 同符号の数の乗算ならば、答えの符号はプラス(+)
- 異符号の数の乗算ならば、答えの符号はマイナス(-)
- 答えの数字(絶対値)は、どちらのときでも乗算する数の数字(絶対値)の積
ちなみに、この符号の規則性は除算でも成り立つので、乗算に置き換える前でも答えの符号を求めることができます。慣れてくればその解き方でも構いません。
規則性を上手に使おう。まずは乗算を完璧に。
以上を踏まえて、先ほどの例題を解いてみましょう。
例題(1)の解答・解説
例題(1)
\begin{align*} \quad \left(+2.1 \right) \times \left(-0.8 \right) \end{align*}扱う数が小数であっても手順は変わりません。与式の符号の組合せを見て、答え(積)の符号を決めましょう。
異符号の数の乗算なので、答えの符号はマイナス(-)です。答えの符号が決まった時点ですぐにイコールのあとに書いておきます。
例題(1)の解答例 1⃣
\begin{align*} \quad &\left(+2.1 \right) \times \left(-0.8 \right) \\[ 7pt ] = \ &- \end{align*}異符号の2数の乗算なら、積の符号はマイナス。
答えの符号が決まったら、数字(絶対値)だけで乗算します。その結果が答えの数字(絶対値)となります。
符号のあとにカッコを書き、その中に数字だけの乗算の式を書きます。カッコを使うのは、符号と数字をはっきり区別するためです。
例題(1)の解答例 2⃣
\begin{align*} \quad &\left(+2.1 \right) \times \left(-0.8 \right) \\[ 7pt ] = \ &-\left(2.1 \times 0.8 \right) \end{align*}カッコ内の乗算を行います。小数の乗算なので、小数点の位置取りに注意しましょう。暗算が難しいときは筆算しましょう。小数の乗算が終われば計算終了です。
例題(1)の解答例 3⃣
\begin{align*} \quad &\left(+2.1 \right) \times \left(-0.8 \right) \\[ 7pt ] = \ &-\left(2.1 \times 0.8 \right) \\[ 7pt ] = \ &-1.68 \end{align*}加算と同じように、乗算でも符号と数字を分けて扱うことが分かります。
初めのうちは計算過程を考えながら記述していきましょう。自分の考えを数式に変換する作業なので、とても大切です。
例題(2)の解答・解説
例題(2)
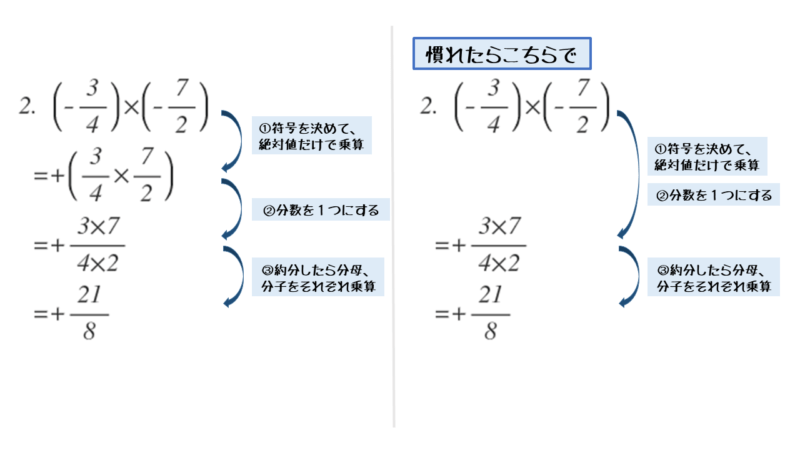
\begin{align*} \quad \left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \end{align*}例題(1)で小数だったのが、例題(2)で分数に変わっただけです。同じ要領で計算できます。与式の符号の組合せを見て、答え(積)の符号を決めましょう。
同符号の数の乗算なので、答えの符号はプラス(+)です。答えの符号が決まった時点ですぐにイコールのあとに書いておきます。
例題(2)の解答例 1⃣
\begin{align*} \quad &\left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \\[ 7pt ] = \ &+ \end{align*}同符号の2数の乗算なら、積の符号はプラス。
答えの符号が決まったら、数字(絶対値)だけで乗算します。その結果が答えの数字(絶対値)となります。
符号のあとにカッコを書き、乗算する数字を書きます。分数の乗算では約分を意識しましょう。
例題(2)の解答例 2⃣
\begin{align*} \quad &\left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \\[ 7pt ] = \ &+\left(\frac{3}{4} \times \frac{7}{2} \right) \end{align*}分数の乗算では、1つの分数にまとめた方が分母の数字と分子の数字を区別しやく計算ミスを減らせます。約分できるかどうかも確認しましょう。
例題(2)の解答例 3⃣
\begin{align*} \quad &\left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \\[ 7pt ] = \ &+\left(\frac{3}{4} \times \frac{7}{2} \right) \\[ 7pt ] = \ &+\frac{3 \times 7}{4 \times 2} \end{align*}分数が1つになったことで、これで1つの数と見なせます。ですからカッコを外しても問題ありません。
約分ができなければ、分母と分子それぞれで乗算します。
例題(2)の解答例 4⃣
\begin{align*} \quad &\left(-\frac{3}{4} \right) \times \left(-\frac{7}{2} \right) \\[ 7pt ] = \ &+\left(\frac{3}{4} \times \frac{7}{2} \right) \\[ 7pt ] = \ &+\frac{3 \times 7}{4 \times 2} \\[ 7pt ] = \ &+\frac{21}{8} \\[ 7pt ] = \ &\frac{21}{8} \end{align*}答えの符号はプラスであれば省略できます。ここでは最後に省略しましたが、慣れてくれば最初から省略しても構いません。
慣れてくれば、いくつか計算過程を省略しても良いでしょう。
高校数学では、除算しても割り切れない場合がほとんどです。ですから、分数をよく扱います。除算して割り切れたときはラッキーくらいに考えておきましょう。
高校数学では、分数の扱いに慣れておいた方が絶対に有利です。
例題(3)の解答・解説
例題(3)
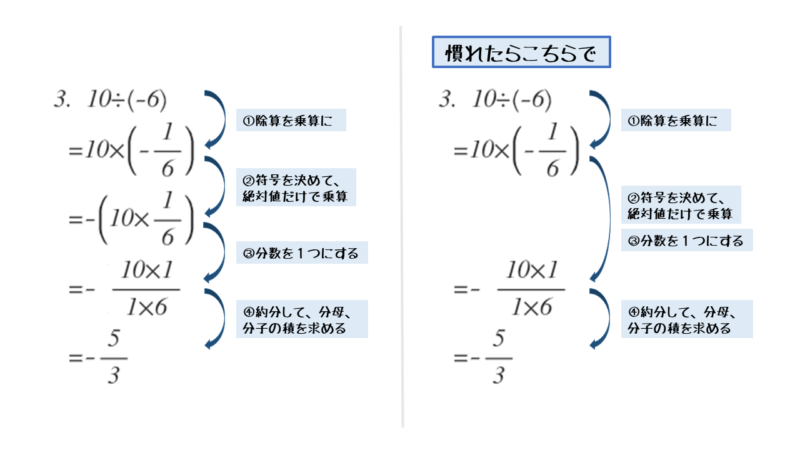
\begin{align*} \quad 10 \div \left(-6 \right) \end{align*}まずは除算を乗算に置き換えましょう。除算でも符号の規則性は乗算と同じです。しかし、四則混合算も扱うようになるので、今のうちに置き換えに慣れておきましょう。
除算を乗算に置き換えるには、割る数の逆数を取る必要があります。逆数は、元の数の分母と分子を入れ替えた数のことです。逆数を元の数に掛けると1になります。
割る数を逆数にして乗算に置き換えます。
例題(3)の解答例 1⃣
\begin{align*} \quad &10 \div \left(-6 \right) \\[ 7pt ] = \ &10 \times \left(-\frac{1}{6} \right) \end{align*}乗算に置き換えた後は、例題(1),(2)と同じ流れで計算していきます。
異符号の数の乗算なので、答えの符号はマイナス(-)です。答えの符号が決まった時点ですぐにイコールのあとに書いておきます。
例題(3)の解答例 2⃣
\begin{align*} \quad &10 \div \left(-6 \right) \\[ 7pt ] = \ &10 \times \left(-\frac{1}{6} \right) \\[ 7pt ] = \ &- \end{align*}符号のあとにカッコを書き、乗算する数字を書きます。分数の乗算では約分を意識しましょう。
例題(3)の解答例 3⃣
\begin{align*} \quad &10 \div \left(-6 \right) \\[ 7pt ] = \ &10 \times \left(-\frac{1}{6} \right) \\[ 7pt ] = \ &-\left(10 \times \frac{1}{6} \right) \end{align*}整数と分数の乗算では、1つの分数にまとめておかないと計算ミスをしがちです。
例題(3)の解答例 4⃣
\begin{align*} \quad &10 \div \left(-6 \right) \\[ 7pt ] = \ &10 \times \left(-\frac{1}{6} \right) \\[ 7pt ] = \ &-\left(10 \times \frac{1}{6} \right) \\[ 7pt ] = \ &-\frac{10 \times 1}{6} \end{align*}約分してから乗算しましょう。
例題(3)の解答例 5⃣
\begin{align*} \quad &10 \div \left(-6 \right) \\[ 7pt ] = \ &10 \times \left(-\frac{1}{6} \right) \\[ 7pt ] = \ &-\left(10 \times \frac{1}{6} \right) \\[ 7pt ] = \ &-\frac{10 \times 1}{6} \\[ 7pt ] = \ &-\frac{5}{3} \end{align*}慣れてきたらいくつか計算過程を省略しましょう。
例題(2)と同じく分数の乗算が出てくるので、約分を意識して計算しましょう。
第4問の解答・解説
例題(4)
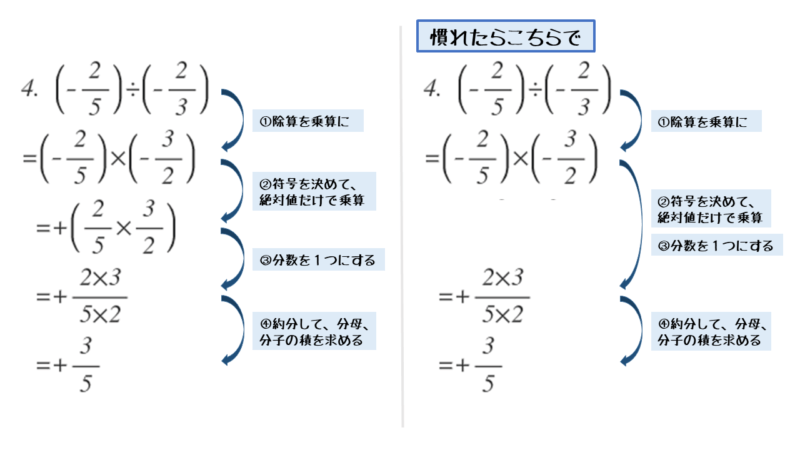
\begin{align*} \quad \left(-\frac{2}{5} \right) \div \left(-\frac{2}{3} \right) \end{align*}例題(4)は、分数の除算です。例題(4)と同じ要領で、割る数の逆数をとって乗算に置き換えます。あとは乗算の手順に従って計算します。
例題(4)の解答例
\begin{align*} \quad &\left(-\frac{2}{5} \right) \div \left(-\frac{2}{3} \right) \\[ 7pt ] = \ &\left(-\frac{2}{5} \right) \times \left(-\frac{3}{2} \right) \\[ 7pt ] = \ &+\left(\frac{2}{5} \times \frac{3}{2} \right) \\[ 7pt ] = \ &+\frac{2 \times 3}{5 \times 2} \\[ 7pt ] = \ &+\frac{3}{5} \\[ 7pt ] = \ &\frac{3}{5} \end{align*}慣れたらいくつか計算過程を省略しましょう。
例題の乗算や除算では、2数だけの基本的な計算です。このようなレベルの計算問題で、符号の規則性を覚え、計算の流れを把握しましょう。
易しい計算で、符号の規則性や計算の流れをマスターしよう。
次は、3つ以上の数の乗除算に挑戦してみましょう。