中学数学｜正負の数の乗除算を解いてみよう

08/30/2023中学数学

３つ以上の数の乗除算

次の乗除算を解いてみましょう。

問

\begin{align*} &(1) \quad \left(-2 \right) \times \left(+3 \right) \times \left(-4 \right) \\[ 7pt ] &(2) \quad \left(-5 \right)^{2} \\[ 7pt ] &(3) \quad -{5^{2}} \end{align*}

正負の数の乗除算では、扱う数が３つ以上になると計算をラクにするために符号の規則性に注目する必要があります。

問(1)では、３つの数の乗算を扱っています。問(2)，(3)では、３つ以上の数を扱っていませんが、符号の規則性を扱っています。

問(1)の解答・解説

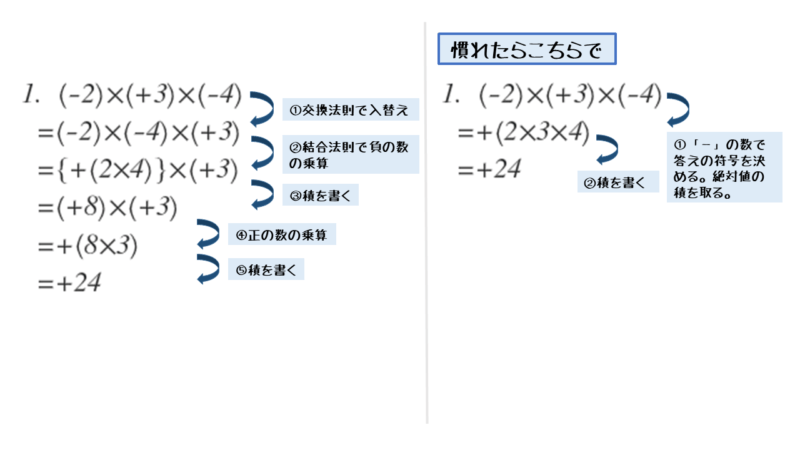
問(1)

\begin{align*} \quad \left(-2 \right) \times \left(+3 \right) \times \left(-4 \right) \end{align*}

３つ以上の乗除算は、２数の乗除算の繰り返し

３つ以上の数の乗除算は、２数の乗除算の繰り返しで解くことができます。

３つ以上の数の乗除算

除算があれば、乗算に置き換える。
交換法則や結合法則を利用して、同符号の２数の乗算を先に行う。
さいごに異符号の２数の乗算を行う。

計算の流れは加算のときと変わらないことが分かります。加算と同じように、同符号の２数の乗算であれば答えの符号がプラスとなるので、もし符号を忘れたとしても問題が起きにくいからです。

基本的な流れで計算すると過程が長くなりますが、以降の解き方につながるので、この考え方を覚えておいて損はありません。

符号の規則性を利用する

３つ以上の数を乗算するときでもできるだけ簡単に解くには、符号の規則性を利用します。

乗算では、乗算する数の符号の組合せで答え（積）の符号が決まるという規則性があります。式の中にあるマイナス（－）の個数に注目すると、以下のような規則性があります。

マイナスの個数で決まる規則性

式の中にマイナス（－）が奇数個あるとき、答え（積）の符号はマイナス（－）
式の中にマイナス（－）が偶数個あるとき、答え（積）の符号はプラス（＋）

マイナスの個数が偶数個ならば、負の数どうしの積が複数組できる。その積の符号はどれもプラスとなる。

マイナス（－）の符号に注目した乗算は、もちろん２数のときでもできます。

正負の数を扱うとき、よくあるミスが符号の扱いなので、符号に注目して計算することは良いことだと思います。

計算過程は以下のようになります。左側が２数の乗算を繰り返す基本的な解法です。右側がマイナスの個数で決まる規則性を利用した解法（「慣れたらこちらで」）です。

最終的には右側の解法で解けるようになりましょう。

問(2)，(3)の解答・解説

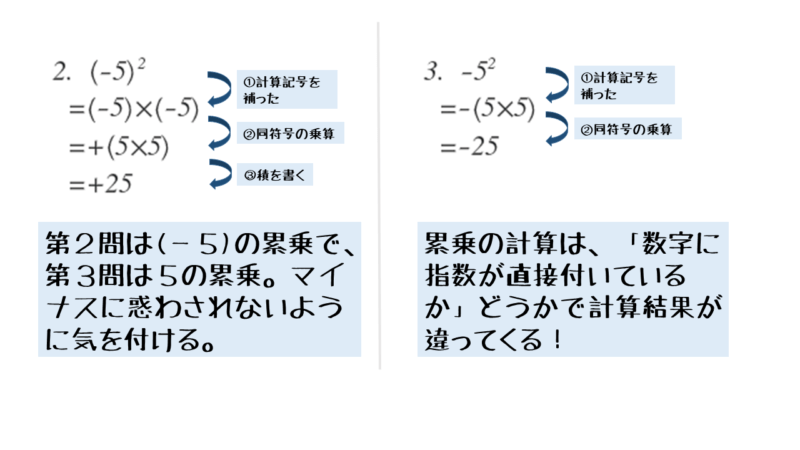
問(2)，(3)

\begin{align*} &(2) \quad \left(-5 \right)^{2} \\[ 7pt ] &(3) \quad -{5^{2}} \end{align*}

上述のように、３つ以上の数を乗算するときには符号の規則性を利用します。ただし、問(2)，(3)のような計算が含まれると、よく符号のミスをします。

累乗について

問(2)では、－５を２乗しており、問(3)では、５を２乗しています。累乗は同じ文字や数の乗算を表します。

数字の右肩にある小さな数字は指数と言い、同じ数を何個（何回）掛けているかを表します。この指数を用いると、同じ数の乗算を簡略化して表記できるようになります。

「累」は累計や累加といった言葉のように、重ねるや繰り返すなどの意味を持つ言葉。そこから転じて、累乗は同じ数を繰り返し乗算する意味だと考えられる。累乗も数式を簡略化して表すための工夫の１つ。

累乗を乗算に書き換えてみると、どんな数をいくつ掛け合わせているのかが良く分かります。

累乗を乗算に書き換える

\begin{align*} (2) \quad &\left(-5 \right)^{2} \\[ 7pt ] = \ &\left(-5 \right) \times \left(-5 \right) \\[ 10pt ] (3) \quad &-{5^{2}} \\[ 7pt ] = \ &-\left(5 \times 5 \right) \end{align*}

指数がカッコの右上に付いている場合と、数字の右上に付いている場合とで意味が異なることが分かります。負の数の累乗であれば、負の数をカッコでくくり、そのカッコの右上に指数を書きましょう。

累乗の表記は、指数の付き方で意味が全く異なるので注意しよう。符号のミスが多いものの１つ。

累乗の計算

問(2)では、目に見えるマイナスの符号は１個だけです。しかし、－５の２乗とは－５を２回掛け合わせるという意味なので、実際にはマイナスの符号が２個あります。ですから積の符号はプラスの符号になります。

問(2)の解答例

\begin{align*} \quad &\left(-5 \right)^{2} \\[ 7pt ] = \ &\left(-5 \right) \times \left(-5 \right) \\[ 7pt ] = \ &+\left(5 \times 5 \right) \\[ 7pt ] = \ &+25 \\[ 7pt ] = \ &25 \end{align*}

問(3)では、目に見えるマイナスの符号は１個だけです。しかも、このマイナスの符号は乗算には関与しません。なぜなら、５の２乗とは５を２回掛け合わせるという意味だからです。

問(3)の解答例

\begin{align*} \quad &-{5^{2}} \\[ 7pt ] = \ &-\left(5 \times 5 \right) \\[ 7pt ] = \ &-\left(+25 \right) \\[ 7pt ] = \ &+\left(-25 \right) \\[ 7pt ] = \ &-25 \end{align*}

累乗の計算に関係がないマイナスの符号はそのままにしておきます。カッコ内の乗算は正の数どうしの乗算なので、積の符号がプラスの符号になります。その結果、ー（＋２５）となります。正の数の減算から負の数の加算に置き換えてカッコを省略すると、－２５になります。

問(2)，(3)の結果の違い

\begin{align*} (2) \quad &\left(-5 \right)^{2} \\[ 7pt ] = \ &+25 \\[ 10pt ] (3) \quad &-{5^{2}} \\[ 7pt ] = \ &-25 \end{align*}

問(2)，(3)では、目に見えているマイナスの符号はともに１個ですが、積の符号は異なります。指数が何に付いているかで結果が変わります。累乗は乗除算だけでなく、四則計算などでも頻出なので、その扱いには細心の注意を払いましょう。

累乗は乗算を簡略化した式なので、「マイナス（－）の個数≠目に見えている個数」。累乗を見かけたら最優先で処理。乗算の計算記号を補った式に置き換えるのが符号ミスを減らすコツ。

計算過程やコツをまとめると以下のようになります。