中学数学|正負の数の加減算を解いてみよう

正負の数の加減算には規則性がありました。その規則性をきちんと利用できるように演習してみましょう。
最初のうちは計算過程をできるだけ残して規則性を確認していくことが大切です。計算の流れが頭に入ったら、どこまで過程を省略できるかを考えながら演習していくと良いでしょう。
「最初は何事も丁寧に。次は速く。最後は丁寧に速く。」を心掛けながら演習しましょう。
加減算を加算に統一
正負の数の減算は加算に置き換えることができます。ですから加減算は加算に統一することが最初のステップです。
次の加減算を考えます。
例題
次の計算をせよ。
\begin{align*} &1. \quad \left(+2 \right)+\left(+4 \right) \\[ 7pt ] &2. \quad \left(+2 \right)+\left(-4 \right) \\[ 7pt ] &3. \quad \left(+2 \right)-\left(+4 \right) \\[ 7pt ] &4. \quad \left(+2 \right)-\left(-4 \right) \end{align*}加減算の方針や解き方
計算問題を解くとき、式をよく観察することが大切です。
計算記号と符号の区別、加算や減算の区別がつきますか? これらを区別できるようになると、問題を解くときに方針を立てやすくなります。
カッコとカッコの間にある+や-が計算記号で、カッコ内の+や-(数字の直前にあるもの)は符号です。
また、前半の2問が加算で、後半の2問が減算です。
例題1,2の解答・解説
例題1,2
次の計算をせよ。
\begin{align*} &1. \quad \left(+2 \right)+\left(+4 \right) \\[ 7pt ] &2. \quad \left(+2 \right)+\left(-4 \right) \end{align*}加算の式では、一般に加算の計算記号(+)や数についたカッコが省略されます。その表記に慣れるために、省略した式を書いてから計算します。
例題1,2の解答例
\begin{align*} 1. \quad &\left(+2 \right)+\left(+4 \right) \\[ 7pt ] = \ &+2+4 \\[ 15pt ] 2. \quad &\left(+2 \right)+\left(-4 \right) \\[ 7pt ] = \ &+2-4 \end{align*}加算の計算記号やカッコを外すと、与式は正負の数が並んだ式になります。多項式もこれと同じです。
次は2数を加算します。加算する2数について、符号や数字(=絶対値)に着目して計算します。
加算する2数の符号が同符号のとき
- 加算後の符号は、2数と同じ符号
- 加算後の数字(=絶対値)は、2数の数字(=絶対値)の和
加算する2数の符号が異符号のとき
- 加算後の符号は、絶対値が大きい数の符号
- 加算後の数字(=絶対値)は、2数の数字(=絶対値)の差
※差は、一般に大きい方から小さい方を引く計算。
例題1,2の計算過程は以下のようになります。慣れてきたら、暗算で済ませて過程を省略しましょう。
計算過程を下に記述していくのがコツです。縦書きは、横書きよりも式の移り変わりを把握しやすいので、計算ミスを減らせます。
例題3,4の解答・解説
例題3,4
次の計算をせよ。
\begin{align*} 3. \quad \left(+2 \right)-\left(+4 \right) \\[ 7pt ] 4. \quad \left(+2 \right)-\left(-4 \right) \end{align*}例題3,4は減算なので、まず加算に置き換えます。減算を加算に置き換えるとき、減算の計算記号と、その後ろにある数の符号との組合せに応じて置き換えます。
減算から加算への置き換え
- 「正の数を引く」は、「負の数を足す」に(例題3)
- 「負の数を引く」は、「正の数を足す」に(例題4)
例題では以下のようになります。
例題3,4の解答例
\begin{align*} 3. \quad &\left(+2 \right)-\left(+4 \right) \\[ 7pt ] = \ &\left(+2 \right)+\left(-4 \right) \\[ 15pt ] 4. \quad &\left(+2 \right)-\left(-4 \right) \\[ 7pt ] = \ &\left(+2 \right)+\left(+4 \right) \end{align*}加算に置き換えたら、例題1,2と同じ要領で計算します。
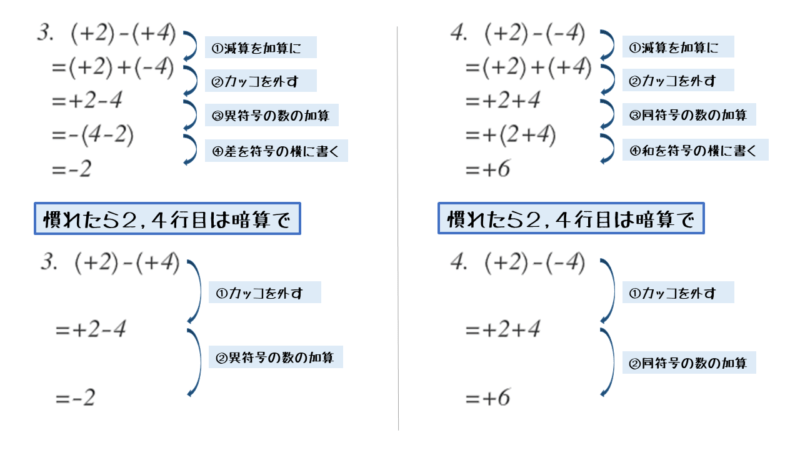
例題3,4の計算過程は以下のようになります。慣れてきたら、暗算で済ませて過程を省略しましょう。
なお、例題4の決算結果+6は、符号を省略した6でも構いません(省略するのが一般的)。ただし、負の符号(-,マイナス)を省略することはできません。
このような計算は、文字を含む整式でも行います。数だけの計算できちんと規則性や計算の流れをマスターしておきましょう。
次は、3つ以上の数の加減算に挑戦してみましょう。